Презентация на тему Функция тангенса

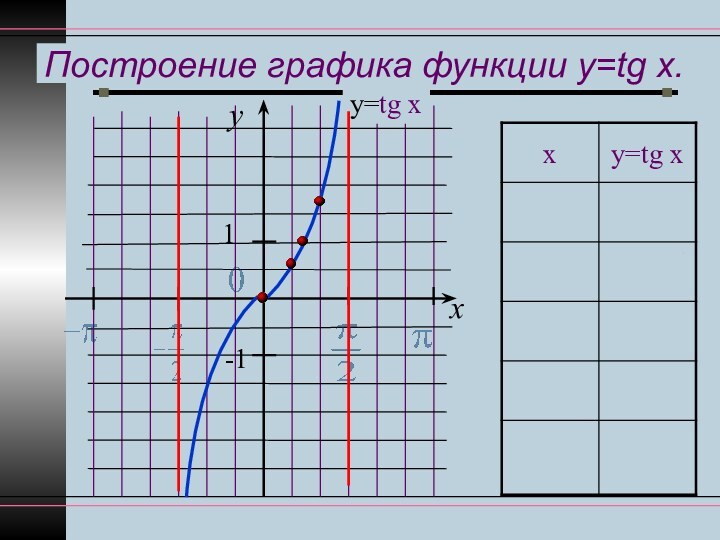
строить график функции у=tgx, используя данные свойства функции.
на основе

анализа графика определить остальные свойства функции
научиться решать простейшие уравнения и неравенства с помощью графика функции.

.
2. Множество значений функции: уєR.
3. Периодическая, Т= π.
4. Нечётная функция.

хє[0;π/2)

функция у=sin x возрастает на данном
промежутке, то sin

х1< sin x2.

3. Т. к. функция у=соs x убывает на данном
промежутке, то соs х1> соs x2 и

(1)

(2)

4.Умножим нер-во (1) на нер-во (2) :

, т. е. tg x1< tg x2 .

= 0 при х = πn, nєZ
у(х)>0 при

хє (0; π/2) и при сдвиге на πn,nєZ.

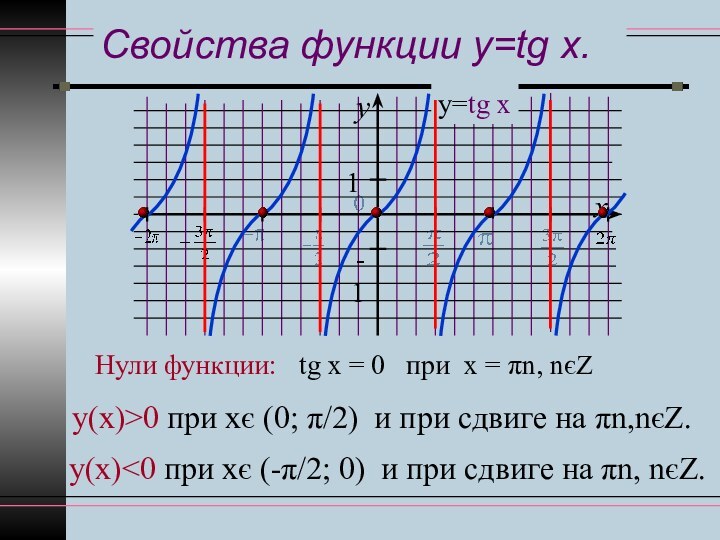
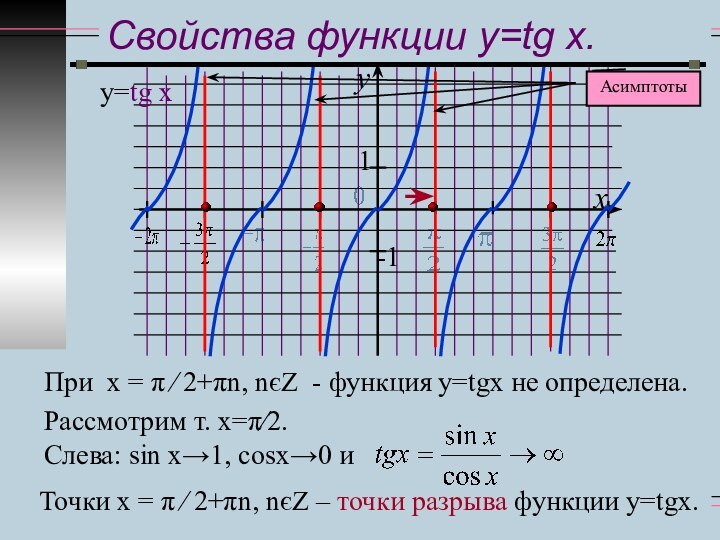
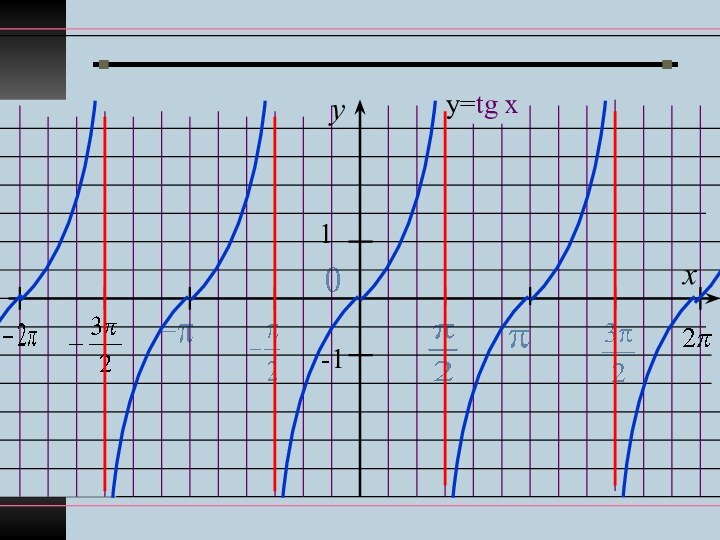
у(х)<0 при хє (-π/2; 0) и при сдвиге на πn, nєZ.

π ∕ 2+πn, nєZ - функция у=tgx не определена.
Рассмотрим

т. х=π∕2.

Слева: sіn x→1, сosx→0 и

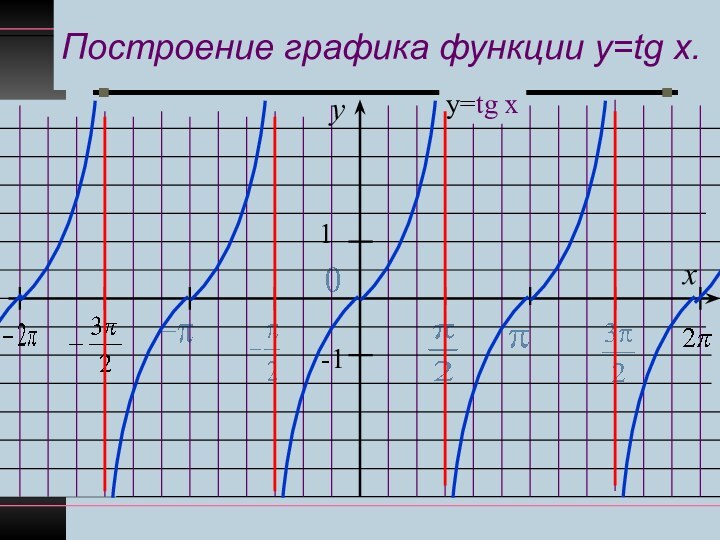
Точки х = π ∕ 2+πn, nєZ – точки разрыва функции у=tgx.

.
2. Множество значений функции: уєR.
3. Периодическая, Т= π.
4. Нечётная функция.
5. Возрастает на всей области определения.
6. Нули функции у (х) = 0 при х = πn, nєZ.
7. у(х)>0 при хє (0; π/2) и при сдвиге на πn,nєZ.
8. у(х)<0 при хє (-π/2; 0) и при сдвиге на πn, nєZ.
9. При х = π ∕ 2+πn, nєZ - функция у=tgx не определена. Имеет точки разрыва графика и асимптоты.

–π ≤ х ≤ 3π ∕ 2.
Решение.
у=tg x
у=2
Построим графики

функций у=tgx и у=2

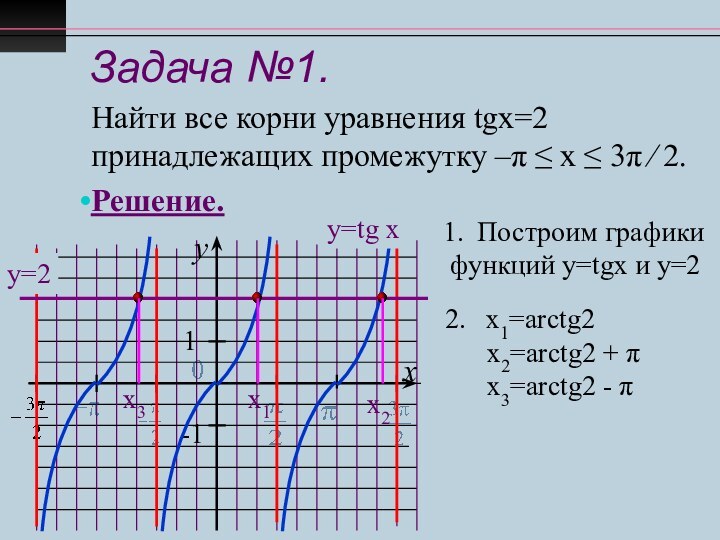
х1=arctg2
х2=arctg2 + π
х3=arctg2 - π

х1

х3

х2

принадлежащих промежутку –π ≤ х ≤ 3π ∕ 2.
Решение.
у=tg

x

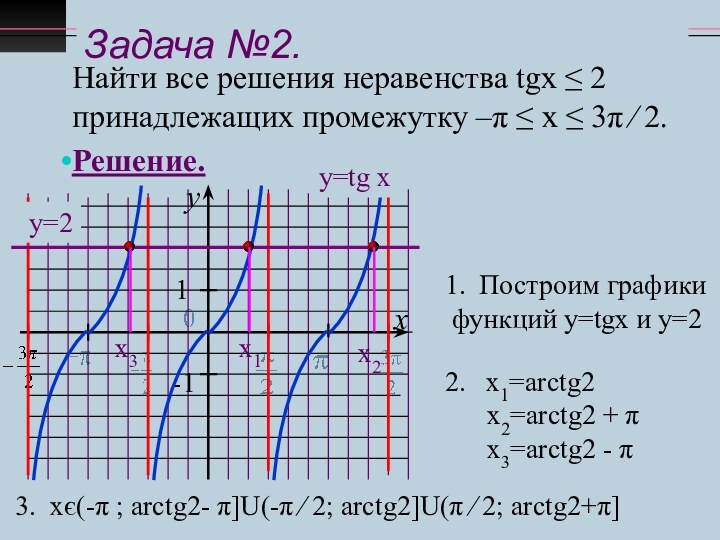
у=2

Построим графики
функций у=tgx и у=2

х1=arctg2
х2=arctg2 + π
х3=arctg2 - π

х1

х3

х2

3. хє(-π ; arctg2- π]U(-π ∕ 2; arctg2]U(π ∕ 2; arctg2+π]