точки вертикальные прямые.
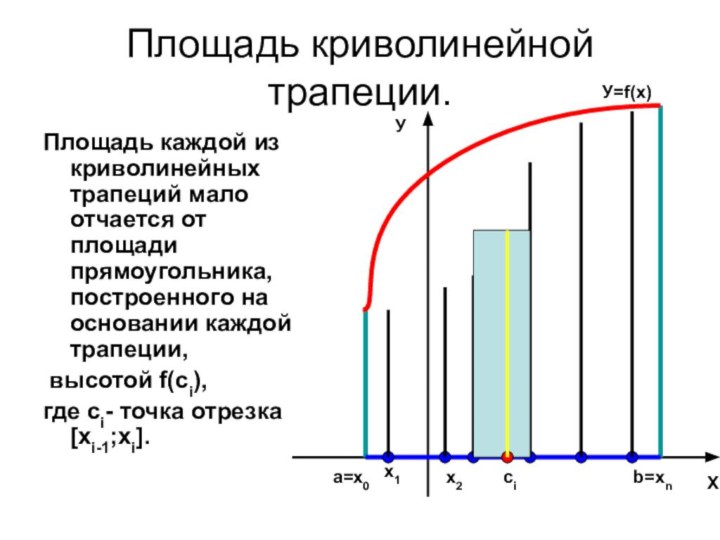
Криволинейная трапеция разбилась на n частей, каждая
из которых- криволинейная трапеция.Х
У
а=х0
b=хn
У=f(x)
х1
х2
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре Криволинейная трапеция
Содержание
- 2. Криволинейная трапеция.Отрезок [a;b]- основание криволинейной трапеции.ХУавУ=f(x)
- 3. Площадь криволинейной трапеции.Разобьём [a;b] на n частей.Проведём
- 4. Площадь криволинейной трапеции.Площадь каждой из криволинейных трапеций
- 5. Площадь криволинейной трапеции. ХУа=х0b=хnУ=f(x)х1х2ci
- 6. Площадь криволинейной трапеции. Sкр. тр.= =S1+ S2+…+ Sn==f(c1)*(x1-x0)+ f(c2)*(x2-x1)+…+ f(cn)*(xn-xn-1)Интегральная сумма функции f(x) на отрезке [a;b]ХУа=х0b=хnУ=f(x)х1х2cic1c2cn
- 7. Площадь криволинейной трапеции. Если увеличивать число точек
- 8. Как же вычислять интегралы?
- 9. Скачать презентацию
- 10. Похожие презентации
Криволинейная трапеция.Отрезок [a;b]- основание криволинейной трапеции.ХУавУ=f(x)
![Криволинейная трапеция.Это фигура, ограниченная снизу отрезком [a;b], сверху- графиком непрерывной функции, принимающей](/img/tmb/7/670062/d9c9f35a7676d9ace134b30e302399c4-720x.jpg "Презентация на тему Криволинейная трапеция.Это фигура, ограниченная снизу отрезком [a;b], сверху- графиком")
![Криволинейная трапеция.Отрезок [a;b]- основание криволинейной трапеции.ХУавУ=f(x)](/img/tmb/7/670062/1e9d9cf91b1e7423840fd11ddb4c9d87-720x.jpg "Презентация по алгебре Криволинейная трапеция")
![Площадь криволинейной трапеции.Разобьём [a;b] на n частей.Проведём через точки вертикальные прямые.Криволинейная трапеция](/img/tmb/7/670062/b96c1223399499cf7ebbc9e6e271854a-720x.jpg "Презентация по алгебре Криволинейная трапеция")
![Площадь криволинейной трапеции. Sкр. тр.= =S1+ S2+…+ Sn==f(c1)*(x1-x0)+ f(c2)*(x2-x1)+…+ f(cn)*(xn-xn-1)Интегральная сумма функции f(x) на отрезке [a;b]ХУа=х0b=хnУ=f(x)х1х2cic1c2cn](/img/tmb/7/670062/72eedc6feb647bcd8c7994f1356be60b-720x.jpg "Презентация по алгебре Криволинейная трапеция")
Слайд 3
Площадь криволинейной трапеции.
Разобьём [a;b]
на n частей.
Проведём через
точки вертикальные прямые.
из которых- криволинейная трапеция.
Слайд 4
Площадь криволинейной трапеции.
Площадь каждой из криволинейных трапеций мало
отчается от площади прямоугольника, построенного на основании каждой трапеции,
высотой f(ci), где ci- точка отрезка [xi-1;xi].
Х
У
а=х0
b=хn
У=f(x)
х1
х2
ci
Слайд 6
Площадь криволинейной трапеции.
Sкр. тр.=
=S1+ S2+…+ Sn=
=f(c1)*(x1-x0)+
f(c2)*(x2-x1)+…+ f(cn)*(xn-xn-1)
Интегральная сумма функции f(x) на отрезке [a;b]
Х
У
а=х0
b=хn
У=f(x)
х1
х2
ci
c1
c2
cn
Слайд 7
Площадь криволинейной трапеции.
Если увеличивать число точек разбиения,
то размер разбиения будет стремиться к
нулю, тогда интегральная
сумма будет стремиться к некоторому числу(площади криволинейной трапеции),
которое называется интегралом функции f(x)
на отрезке [a;b] и записывается
Х
У
а=х0
b=хn
У=f(x)
х1
х2
ci
c1
c2
cn
