Презентация на тему Радианная мера углов и дуг

дугу окружности длиной в один радиус (обозначается 1 рад).

1 рад

R

R

R

A

B

O

⋅

⋅

⋅

∪ AB=R
∠AOB=1 рад

600

1 рад

формулу длины окружности…
R

R
R
R
R
R
?

в градусную и наоборот.

Ответ: α0= α0·

рад − правило перевода из градусной меры в радианную;

α рад= α· − правило перевода из радианной меры в градусную.

1 рад = ; 1 рад ≈ 57019’
10 = рад; 10 ≈ 0,017 рад

3600 – 2π рад
10 – х рад

3600 – 2π рад
х 0 – 1 рад

и радиусом, равным единице, называется единичной, а ограниченный ей

круг – тригонометрическим.

Приняв точку пересечения окружности с положительной частью оси Ох за начало отсчета;
Выбрав положительное направление – против часовой стрелки, отрицательное – по часовой стрелке;
Отложив от начала отсчета дугу в 1 рад, мы получим, что тригонометрическая окружность в некотором смысле «эквивалентна» понятию «числовая прямая».

x

y

0

1

1

0

«+»

«−»

1

и на тригонометрической окружности:


Обязательно разберитесь, почему на прямой семь

точек, а на окружности их пять.

длины некоторых из них будут выражены через число π

(объясните почему).

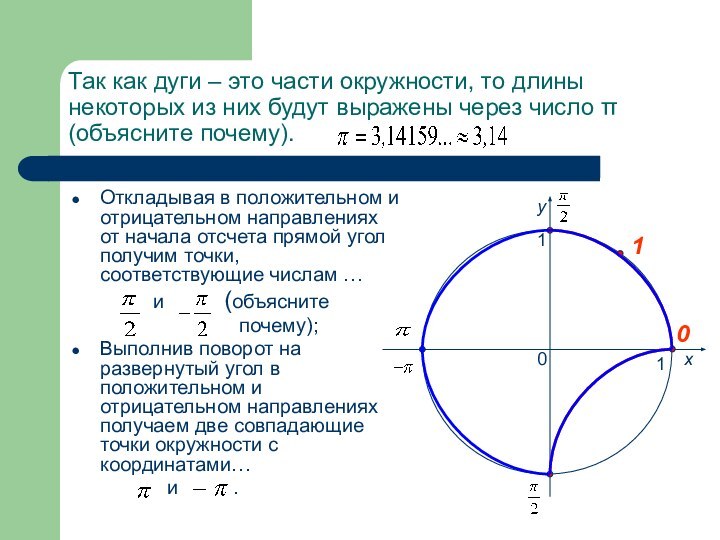
Откладывая в положительном и отрицательном направлениях от начала отсчета прямой угол получим точки, соответствующие числам …
и (объясните
почему);
Выполнив поворот на развернутый угол в положительном и отрицательном направлениях получаем две совпадающие точки окружности с координатами…
и .

x

y

0

1

1

0

1

четыре координатные четверти – I, II, III и IV.
Задание

2. Определите границы координатных четвертей через углы поворота в радианной мере, взятых в положительном направлении.
Задание 3. Выполните предыдущее задание, при условии, что выбирается отрицательное направление углов поворота.
Задание 4. Какой координатной четверти принадлежит точка окружности с координатой 6,28?

x

y

0

1

1

0

1

I

II

III

IV

− это соотношение может Вам понадобиться для

понимания некоторых фактов!

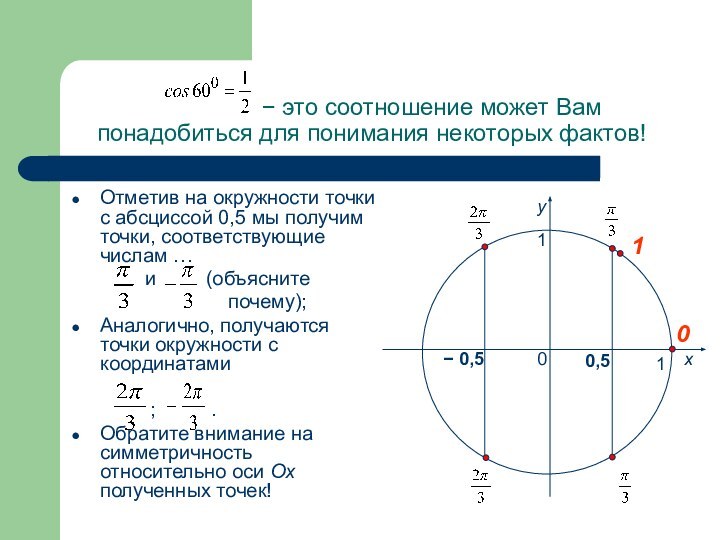
Отметив на окружности точки с абсциссой 0,5 мы получим точки, соответствующие числам …
и (объясните
почему);
Аналогично, получаются точки окружности с координатами

; .
Обратите внимание на симметричность относительно оси Ox полученных точек!

x

y

0

1

1

0

1

0,5

− 0,5

− это соотношение может Вам понадобиться для

понимания некоторых фактов!

Отметив на окружности точки с ординатой 0,5 мы получим точки, соответствующие числам …
и (объясните
почему);
Аналогично, получаются точки окружности с координатами

; .
Обратите внимание на симметричность относительно оси Oy полученных точек!

x

y

0

1

1

0

1

0,5

− 0,5

являющиеся биссектрисами координатных четвертей.
Постройте графики функций y=x и

y=−x. Подумайте, какие углы поворота соответствуют точкам пересечения этих прямых с тригонометрической окружностью?...
…Ответ:
; ; ; .

x

y

0

1

1

0

1

острому положительному углу поворота .
Если добавить полный

поворот к углу α , то мы снова окажемся в той же точке А. Но теперь ее координата равна (подумайте)… .
Вообще, любую точку окружности можно получить поворотом на угол, вида α+2πn, где n∈Ζ и α∈[0;2π).

x

y

0

1

1

0

A(α)

A(α+2π)

которой отмечены наиболее часто встречающиеся в различных таблицах углы.
Примечание.

На чертеже отмечены только положительные углы поворота.
Задание 5. Найдите координаты всех точек, отмеченных на данной окружности (указание: рассмотрите различные прямоугольные треугольники с гипотенузой-радиусом (см.рис.) и примените теорему Пифагора ; помните о симметричности точек).

x

y

0

1

1

0

1

0,5

0,5

-0,5

-0,5

- I четверть,

- II четверть,

- III четверть, - IV четверть.

Задание 3. - I четверть, - II четверть,

- III четверть, - IV четверть

6,28

частей окружности)!

x

y

0

1

1

0

1

2

3

4

5

6

2π