believe, though I shall not live to
see it, when
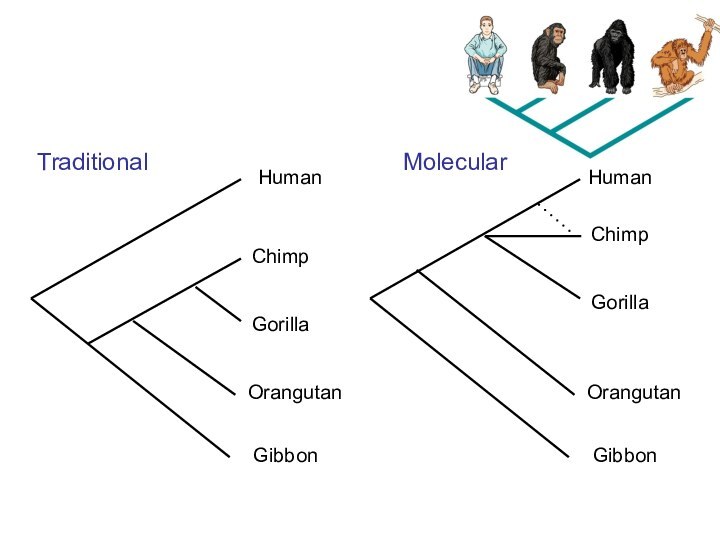
we shall have fairly true genealogical treesof each great kingdom of Nature.
Charles Darwin
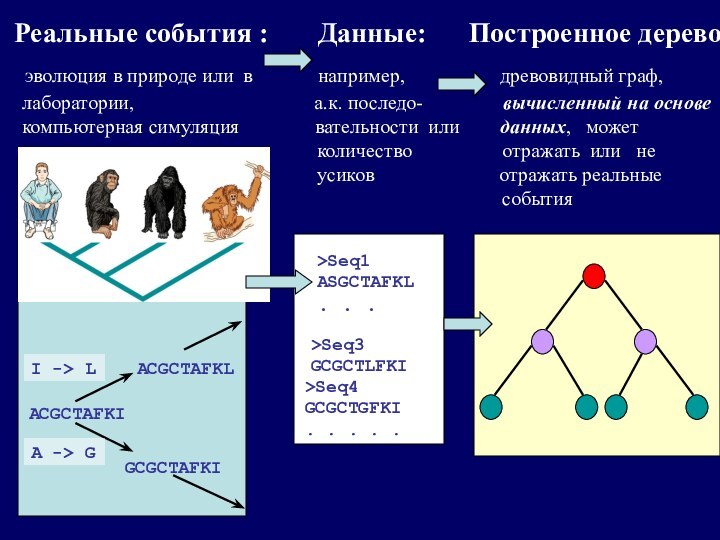
Математическая задача – задача кластеризации,
использование теории графов и комбинаторной оптимизации
для того, чтобы на основе «грязных» биологических данных
получить разумное с точки зрения эксперта-биолога дерево.
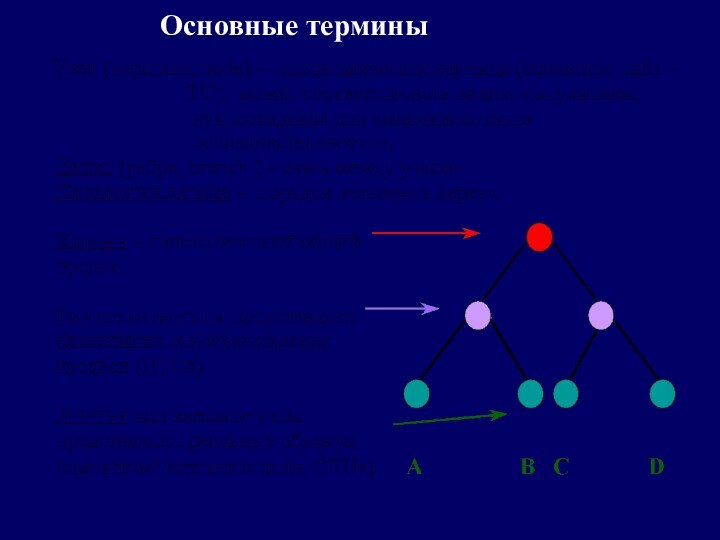
Биологические задачи –
сравнение 3-х и более объектов
(кто на кого более похож .... )
реконструкция эволюции
(кто от кого, как и когда произошел…)