Презентация на тему Популяционная динамика

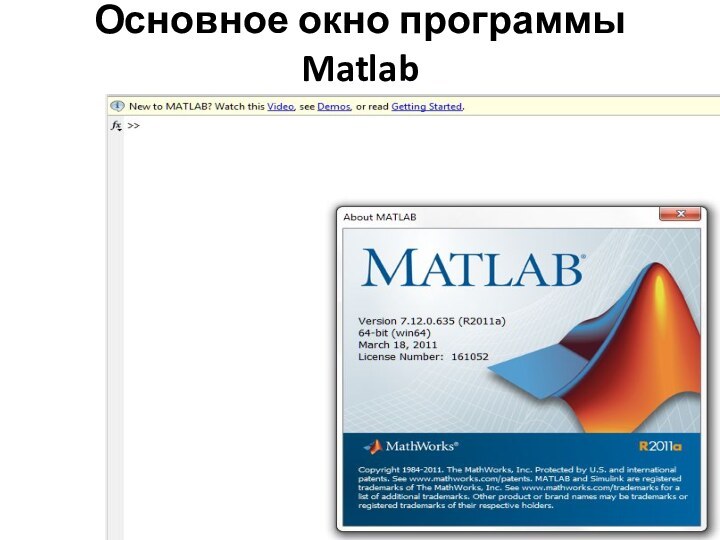
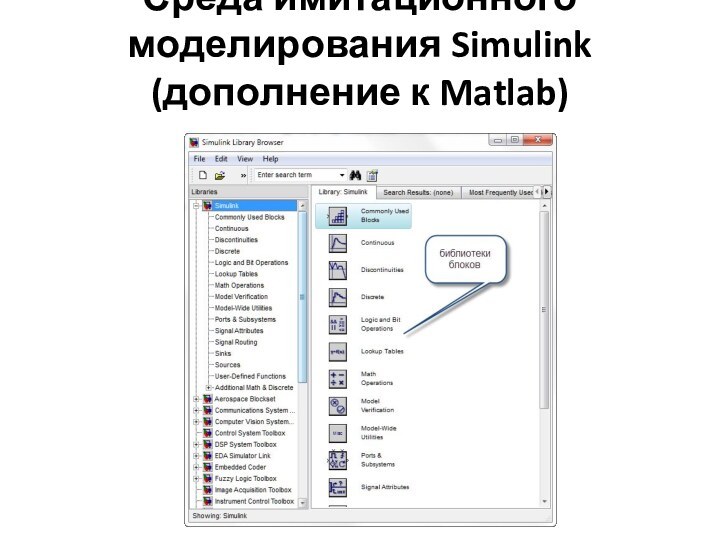
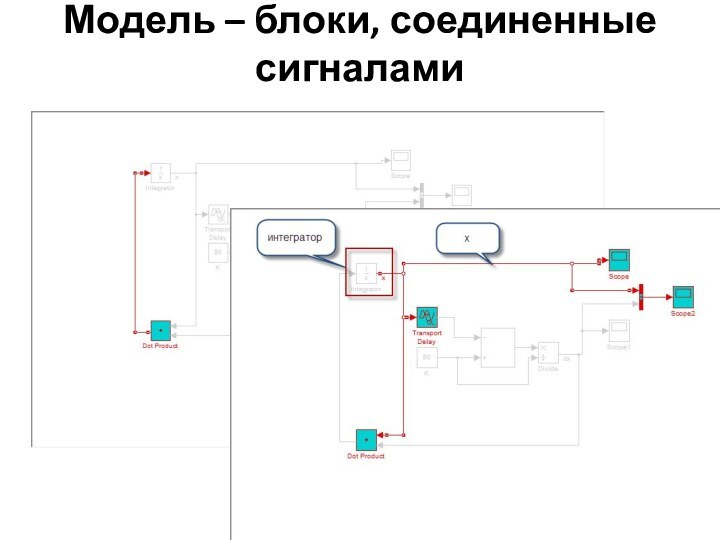
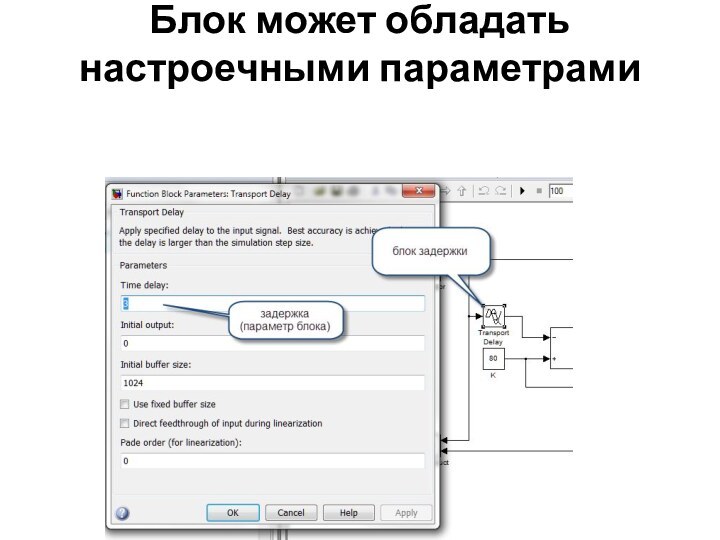
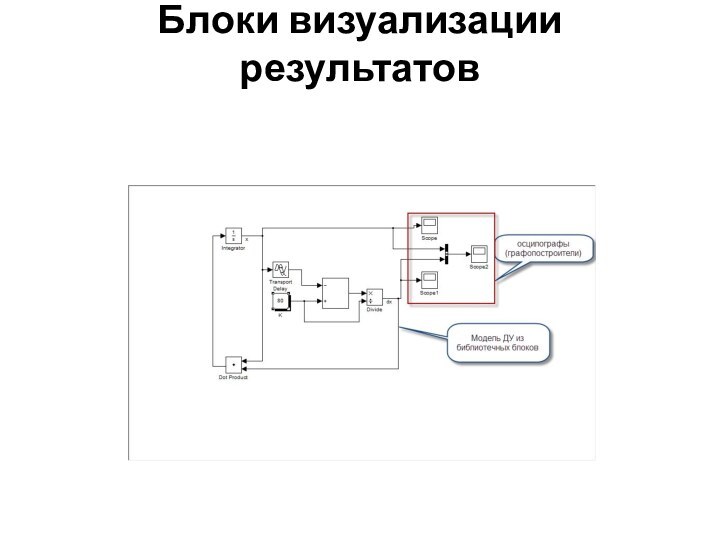
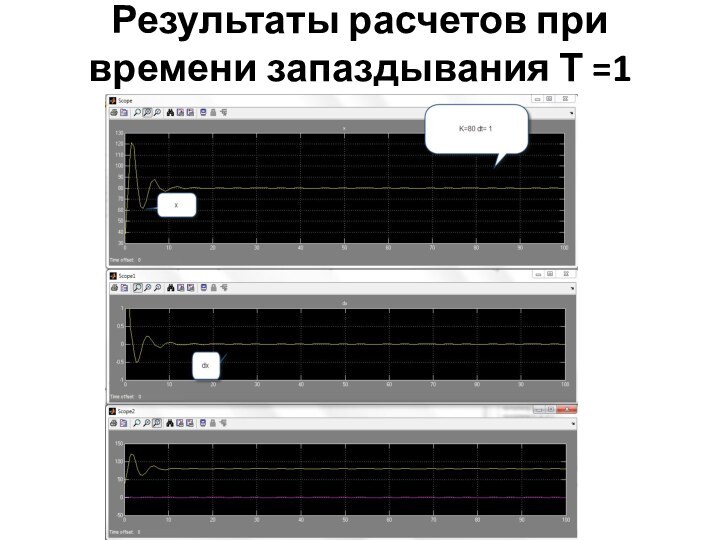
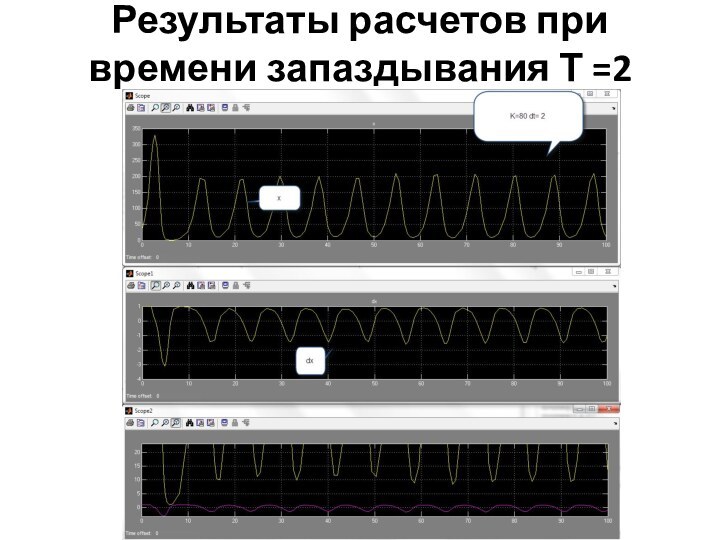
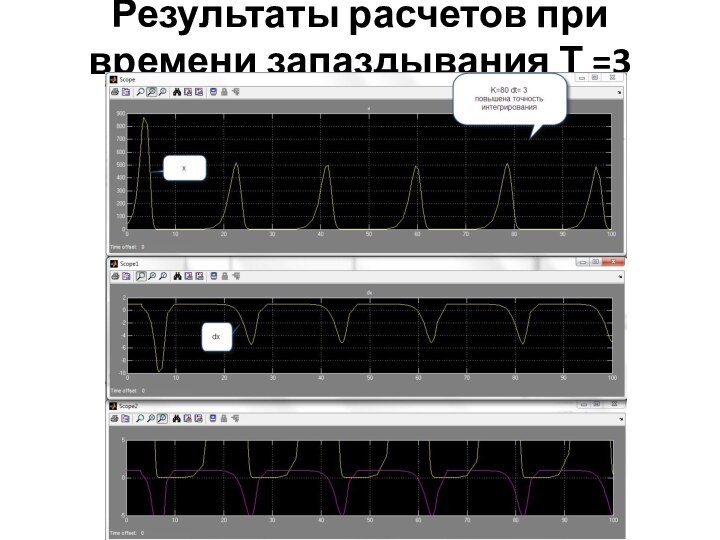
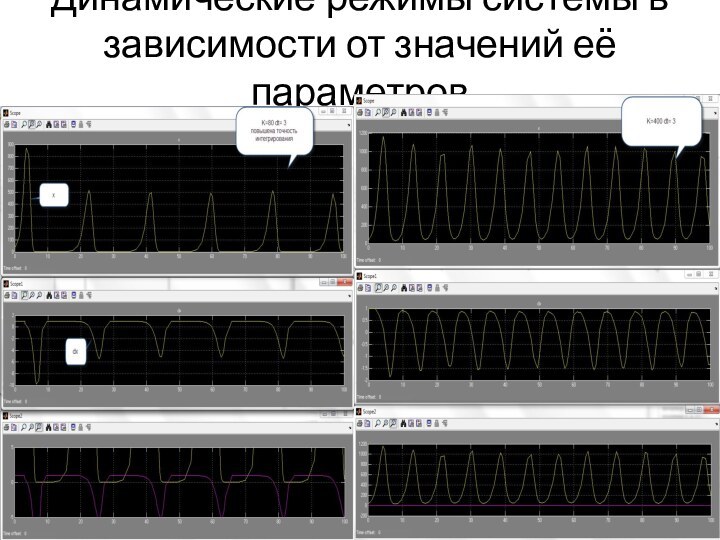
структурой
Условия
Предположим, что:
Ресурсы питания не ограничены.
В начальный момент все

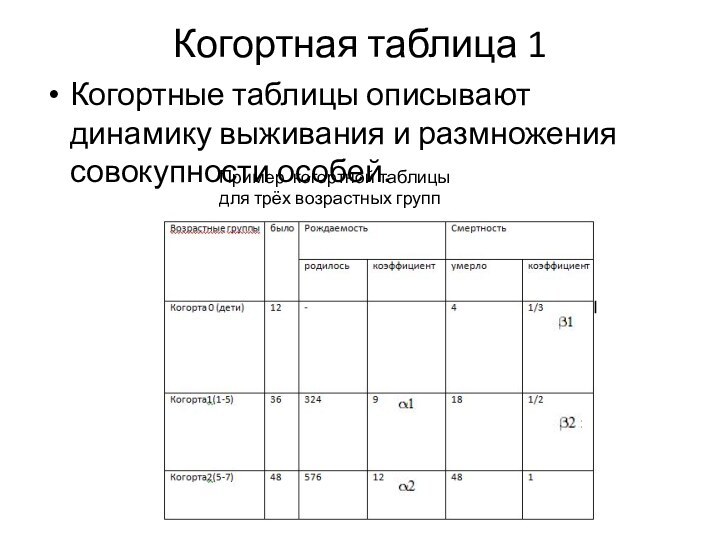
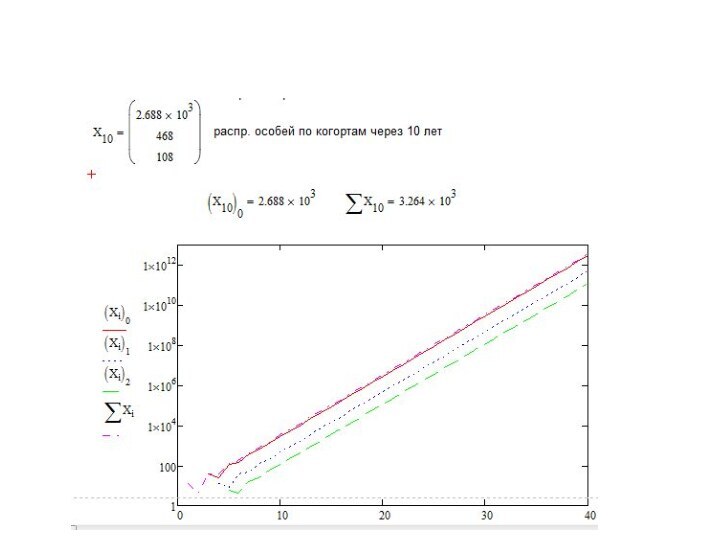
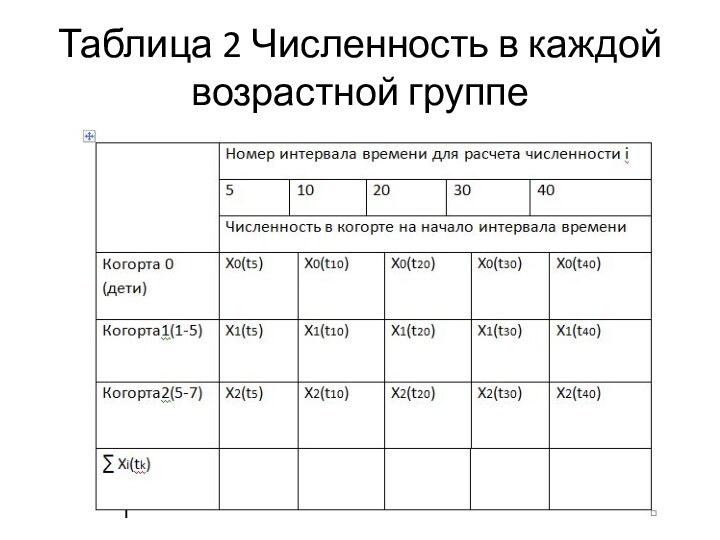
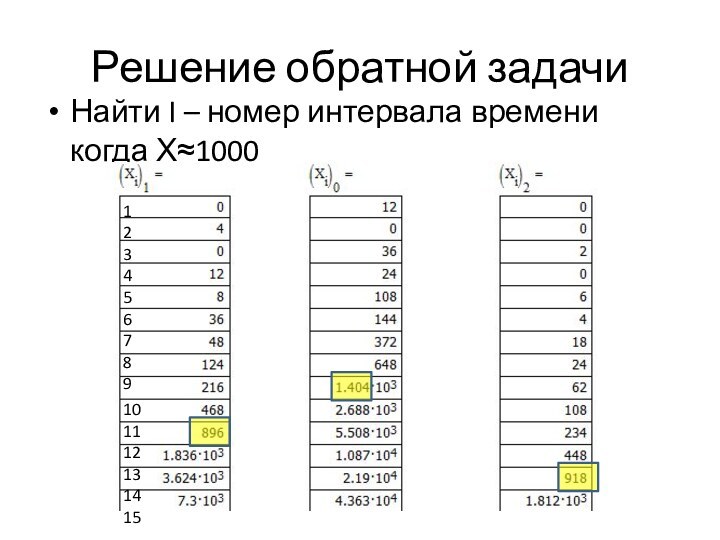
возрастные группы (когорты) могут содержать произвольное число особей.
В начале каждого интервала времени когорты, кроме нулевой(дети), производят потомков в количестве, соответствующем их возрастной плодовитости.
В начале каждого интервала число особей нулевой когорты(детей) равно суммарной плодовитости особей всех остальных когорт.

сокращается из-за смертности.
Выжившие переходят в следующую возрастную группу, т.е.

выжившие особи 0-ой группы образуют в начале следующего интервала 1-ую группу, особи 1-ой группы образуют 2-ую, и так далее вплоть до последней когорты. Последняя когорта полностью вымирает.
Выжившие особи размножаются в начале следующего интервала и образуют нулевую когорту, как это описано выше.

моменты времени t1, t2,…,timax. I – номер интервала
Пусть популяция

содержит n возрастных групп(когорт).
Тогда в каждый фиксированный момент времени (например,t0 ) популяцию можно охарактеризовать вектор-столбцом:



Где число особей первой возрастной группы(когорты) в начале интервала времени t0

характеризует популяцию в следующем интервале времени.

связан с через матрицу перехода L следующим образом:


Далее, чтобы определить численность популяции в последующие интервалы времени, необходимо еще раз перемножить матрицы .

матрица перехода записывается следующим образом:








Значения

коэффициентов рождаемости когорт и коэффициентов смертности переносят из когортной таблицы.

размножения совокупности особей.
Пример когортной таблицы для трёх возрастных групп

1
1
1

возрастных групп вносит наибольший вклад в численность популяции?
Рассчитайте с

помощью модели и покажите на графике численность возрастных групп в начале 5, 10, 20, 40 интервала времени.

когда Х≈1000
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

возрастной структурой
Исходные данные к расчёту Когортная Таблица 1
Исходные данные:

вектор популяции на начало исследования модели , Х0
Результаты расчета - Таблица 2 Численность в каждой возрастной группе в заданные временные интервалы
Гафики зависимости численности когорт от номера интервала времени.
Выводы по графикам (вклад в численность популяции).
Решение обратной задачи: Определение номеров интервалов времени, в которых численность когорт примет заданное преподавателем значение (например, Х=1000). Вывод об относительной скорости достижения заданной численности каждой когорты.

r
Т - время запаздывания

параметров

параметров