Одинаковые буквы он рисует одним цветом, а разные буквы
— разными цветами. Сколько различных цветов ему понадобится?(А) 6
(Б)7
(В) 8
(Г) 9
(Д)10
У
Р
А
К
Е
Н
Г
У
Р
У
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть












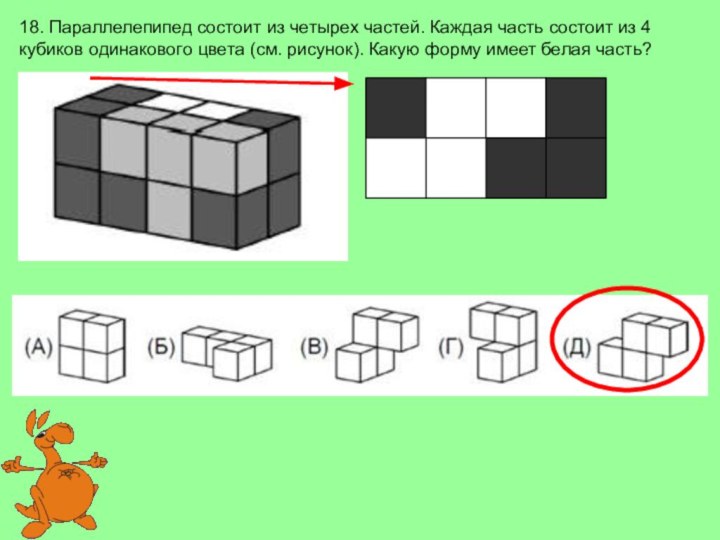




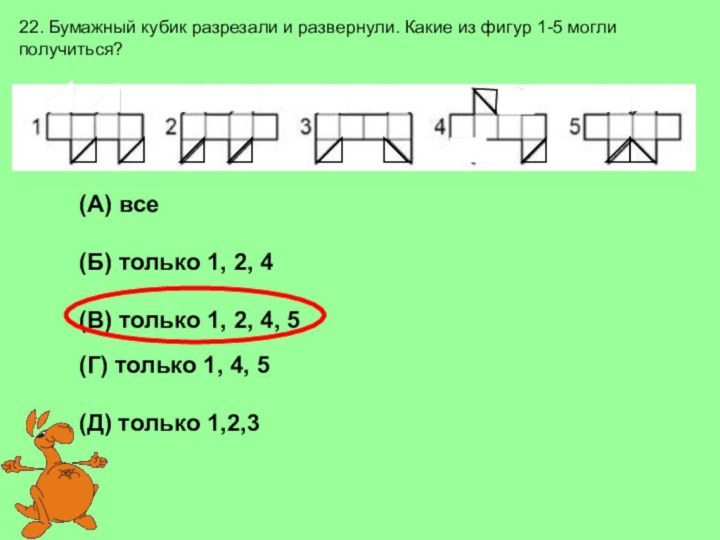





(А) 6
(Б)7
(В) 8
(Г) 9
(Д)10
У
Р
А
К
Е
Н
Г
У
Р
У
(А) 7 час 10 мин
(Б) 7 час 25 мин
(В) 7 час 35 мин
(Г) 7 час 40 мин
(Д) 8 час
получаем 7часов 10 минут.
7часов 50 - 25 минут(те 25 минут на которые спешит первый будильник)=
7часов 25 минут
и отнимаем еще 15 минут от 7 часов 25 минут
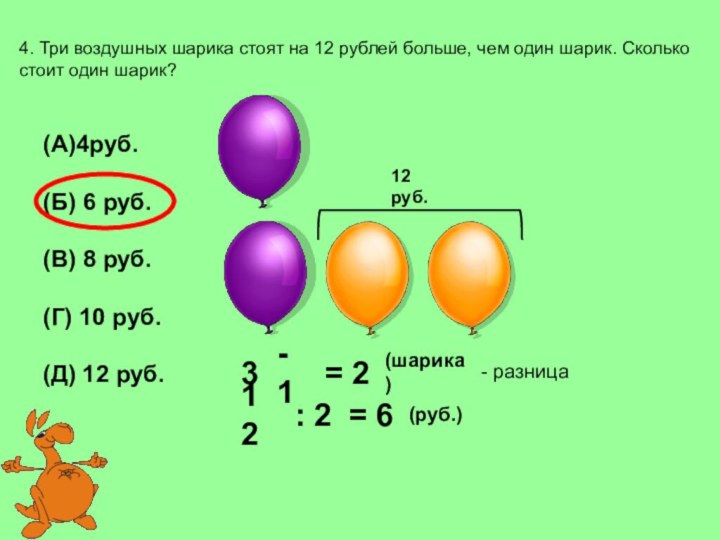
12 руб.
3
- 1
= 2
(шарика)
- разница
12
: 2
= 6
(руб.)
(А) 6
(Б)5
(В) 4
(Г)3
(Д) 2
3
4
2
?
= 44
4 х
2 х
2 х
4 х
+
+
+
12
8
4
4 х ? = 44
+
+
+
24
+
4 х ? = 44
4 х ? =
44 - 24
4 х ? =
20
? =
20 : 4
? = 5
7 дней
Дюжина - 12
- полдюжины 12 : 2 = 6
7 букв
№ 7
7 цветов
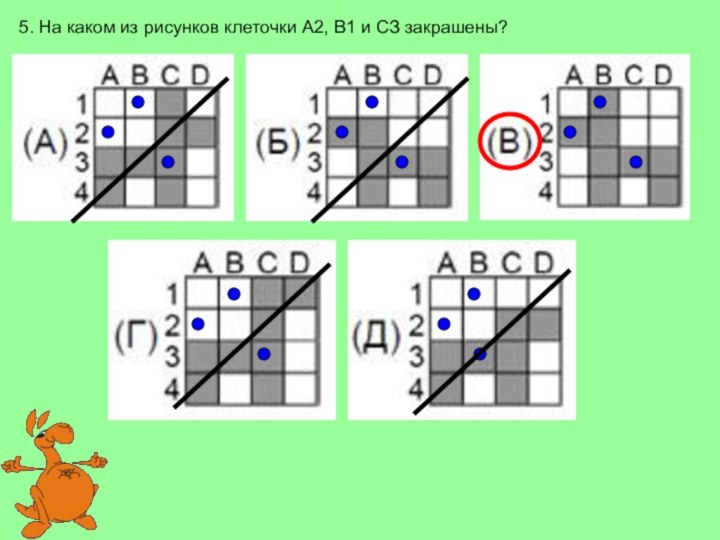
(А) 9
(Б) 8
(В) 7
(Г) 6
(Д) 5
1
2
3
4
5
6
7
(А) 11
(Б) 9
(В) 8
(Г)7
(Д) 5
?
+ 3
(
)
х 50
+ 3
(
)
х 4
= 2012
1
2
3
4
(? + 3 ) х 50 + 3 =
2012 : 4
1
2
3
(? + 3 ) х 50 + 3 =
503
(? + 3 ) х 50 =
503 - 3
(? + 3 ) х 50 =
500
1
2
? + 3 =
500 : 50
? + 3 =
10
? =
10 - 3
? = 7
(А) 19 февраля
(Б) 21 февраля
(В) 23 февраля
(Г) 24 февраля
(Д) 26 февраля
2012 год – високосный, т.к. 2012 : 4
Значит в феврале – 29 дней
20 – 15 = 5 (дней) – которые приходятся
на февраль.
29 – 5 = 24 февраля
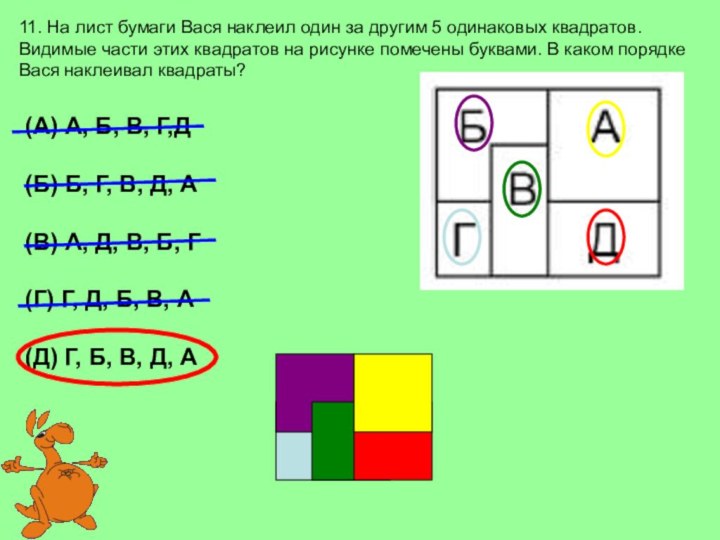
(А) А, Б, В, Г,Д
(Б) Б, Г, В, Д, А
(В) А, Д, В, Б, Г
(Г) Г, Д, Б, В, А
(Д) Г, Б, В, Д, А
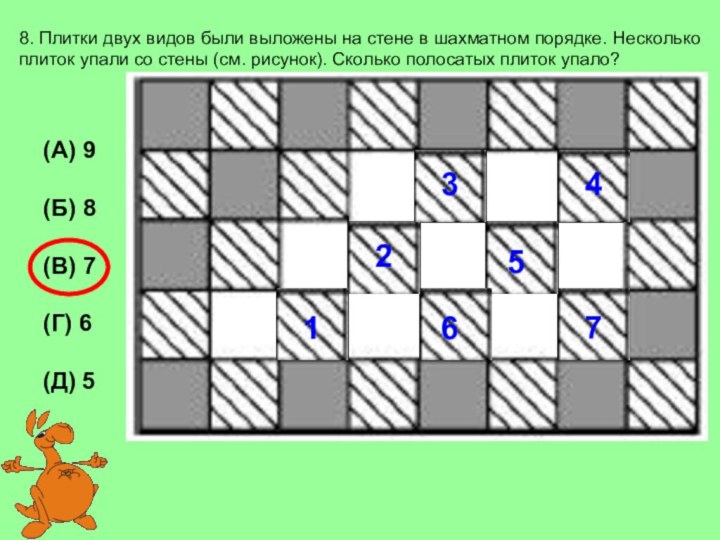
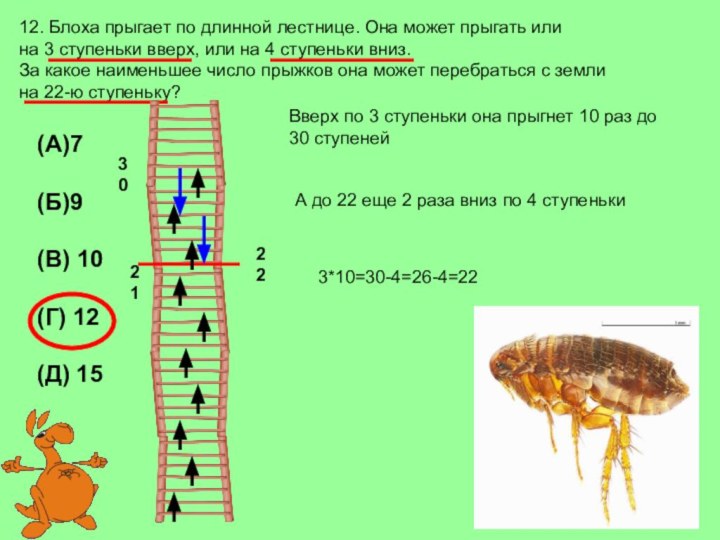
(А)7
(Б)9
(В) 10
(Г) 12
(Д) 15
3*10=30-4=26-4=22
22
Вверх по 3 ступеньки она прыгнет 10 раз до 30 ступеней
А до 22 еще 2 раза вниз по 4 ступеньки
21
30
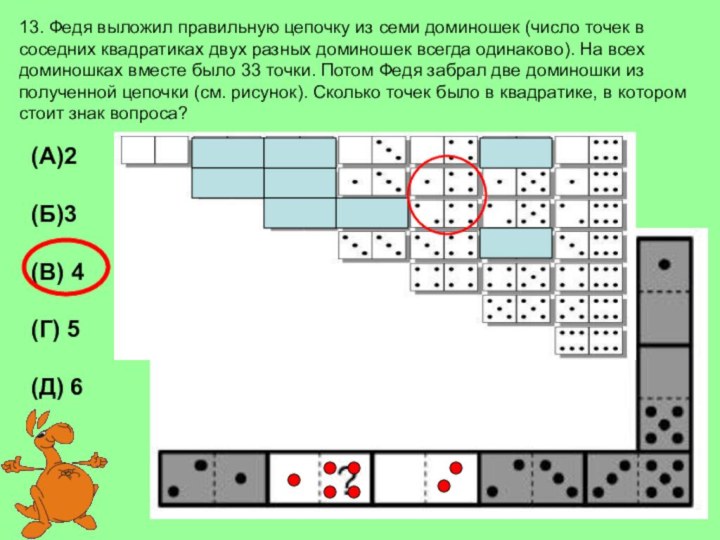
(А)2
(Б)3
(В) 4
(Г) 5
(Д) 6
(А) 15
(Б) 14
(В) 13
(Г) 8
(Д) 7
Кате не было еще и года, а каждый из них прожил по году.
84-42=42,то есть 42 года они прожили втроем с момента её рождения, делим на 3=14.
За один год Катя и родители ВМЕСТЕ проживают 3 года.
Через два года им будет 90,значит сейчас им всем вместе 84
(за два года ВТРОЕМ они прожили 6лет).
За год до рождения им вдвоем было 40,а когда родилась Катя
им втроем было 42
(А) 92
(Б) 94
(В) 95
(Г) 96
(Д) 97
Минимум, который мог получить Миша - 3 балла
Максимум Маши - 97 балов
97 - 3 = 94
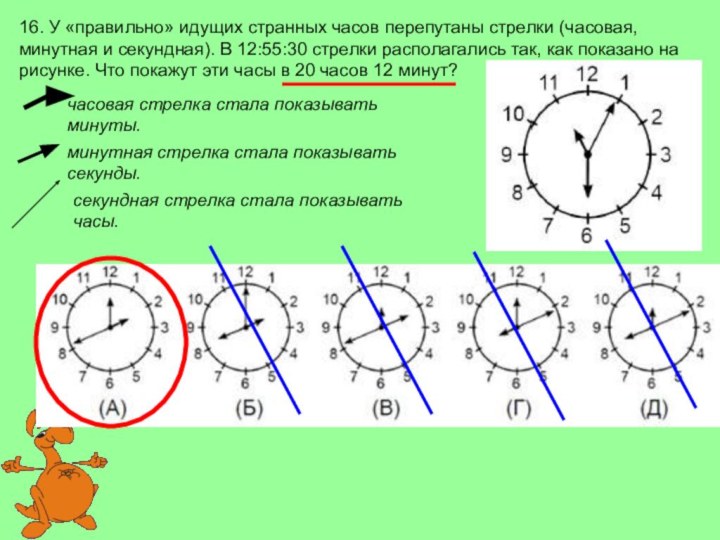
часовая стрелка стала показывать минуты.
минутная стрелка стала показывать секунды.
секундная стрелка стала показывать часы.
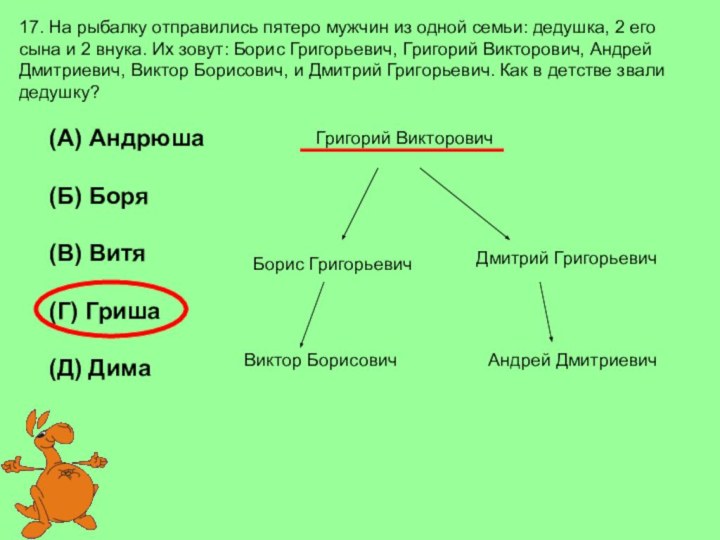
(А) Андрюша
(Б) Боря
(В) Витя
(Г) Гриша
(Д) Дима
Борис Григорьевич
Григорий Викторович
Андрей Дмитриевич
Виктор Борисович
Дмитрий Григорьевич
(А) 12
(Б) 11
(В) 10
(Г)9
(Д) 8
38 - (26 + 2) = 10
- максимальное число игр в которых команда проиграла
80 : 3
Значит 26 игр команда выиграла и 2 – сыграла в ничью
= 26 (ост. 2)
(А) 20000
(Б) 11000
(В) 10100
(Г) 10010
(Д) 10001
=10100 - сумма цифр равна 2
10010+90=10100
10001 (сумма цифр равна 2)
+ 99 (двузначное число)
Пятизначное число: 10010
Двузначное число: 90.
(А) 2
(Б) 3
(В) 4
(Г) 5
(Д) 9
По тому: 4-2=2. человека было ровно на 2-х островах.
Мурано
Бурано
Торчелло
5 человек
9 человек
13 человек
Так как 5 человек посетили Торчелло, следовательно и два остальных острова они тоже посетили.
Поэтому: 13-5=8. Значит, на Мурано побывало 8 человек, помимо тех, кто был и на Торчелло
9-5=4. Значит, на Бурано было только 4 человека, помимо тех, кто был на Торчелло.
Итого: 8-4=4.
Сказано, что было 15 пасажиров которые посетили хотя бы 1 остров, по тому 15-13=2.(значит, 2-е человек были только на Бурано).
(А) 792
(Б) 801
(В) 810
(Г) 890
(Д) 900
Самое большое число должно начинаться с 9 сотен
Самое маленькое число должно начинаться с 1 сотни
Значит в числах должны быть 9 и 1
Наибольшие трёхзначные числа могут быть 901 и 910
910 > 901, значит берём 910
Наименьшие трёхзначные числа могут быть 109 и 190
109 < 190, значит берём 109
910 – 109 =
801
(А) 2
(Б) 3
(В) 4
(Г)5
(Д) 6
Итого: 15/3 = 5.
Путь занимает 6 часов (стража: 1+2+3). Т. е. 6 отрезков.
Скороход за 1 час преодолел 5 отрезков, когда встретил стражу.
Еще через 2 часа скороход (условно) был на 15-м отрезке
(3 часа умножить на 5 отрезков)
А торговец только на 3-м отрезке
(стража, через 3 часа от начала)
В 5 раз быстрее.
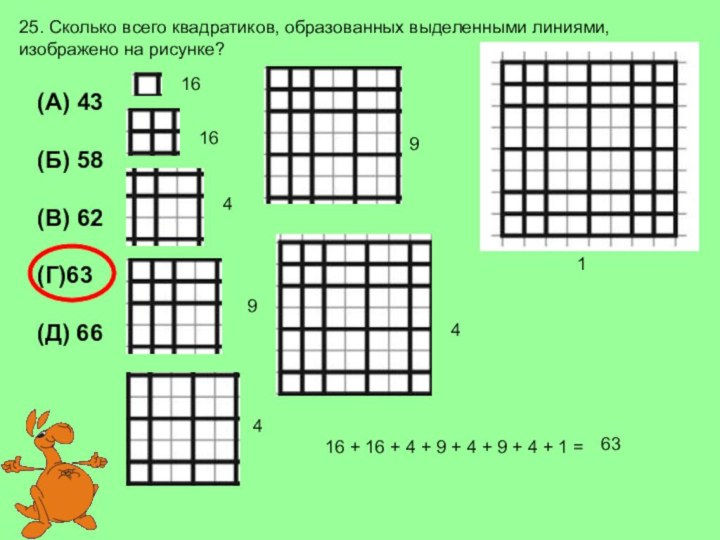
16
16
4
1
4
9
4
9
16 + 16 + 4 + 9 + 4 + 9 + 4 + 1 =
63
(А) 2
(Б) 5
(В) 6
(Г)8
(Д) 9
=> для КЕН самое маленькое из возможных это число 459 => Е=5
Т. к. число КЕН - самое маленькое из возможных, то оно является произведением самых маленьких чисел.
Т. к. разными буквами обозначены разные ненулевые цифры, а одинаковыми буквами - одинаковые цифры, то вторая цифра в первом множителе равна второй цифре во втором множителе, а все остальные цифры - разные.
Цифра У может принимать значения 2, 3, 4, 7, 8, 9.
Пусть У=2, тогда Г и Р могут принимать значения 1 и 7, тогда 864=12*72
Пусть У=3, тогда Г и Р могут принимать значения 1 и 5, тогда 689=13*53.
Пусть У=4, тогда Г и Р могут принимать значения 2 и 3, тогда 816=24*34
Пусть У=7, тогда Г и Р могут принимать значения 1 и 2, тогда 459=17*27
Пусть У=8, тогда Г и Р не могут принимать никаких значений.
Пусть У=9, тогда Г и Р не могут принимать никаких значений.