Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Как вычислять текущую стоимость

Содержание

СодержаниеОценка долгосрочных активовСокращения при расчете PVСложный процентПроцентные ставки и инфляцияПример : Текущая стоимость и облигации
Как вычислять текущую стоимость СодержаниеОценка долгосрочных активовСокращения при расчете PVСложный процентПроцентные ставки и инфляцияПример : Текущая стоимость и облигации Текущая стоимостьКоэфф. дисконтирования == DF = PV для $1Коэффициенты дисконтирования могут использоваться, Текущая стоимость Коэффициенты дисконтирования могут использоваться, чтобы вычислить текущую стоимость любого потока наличности. Текущая стоимость Замена “1” с “t” позволяет использовать Текущая стоимостьПример Вы только что купили новый компьютер за $ 3,000. Условия Текущая стоимостьПример Вы толькочто купили новый компьютер за $ 3,000. Условия платежа Текущая стоимость PVS можно складывать, чтобы оценить многократные потоки наличности. Текущая стоимостьУчитывая два доллара, один получил за год с этого времени и Текущая стоимостьУчитывая два доллара, один получил за год с этого времени и Текущая стоимость Пример Предположим, что потоки наличности от строительства и продажи здания Текущая стоимостьПример - продолжение Предположим, что потоки наличности от строительства и продажи СокращенияИмеются сокращения, которые облегчают вычисление текущей стоимости актива, который выплачивается в различных Сокращения Пожизненная рента- Финансовая концепция, в которой поток наличности теоретически получен навсегда. Сокращения Пожизненная рента - Финансовая концепция, в которой поток наличности теоретически получен навсегда. Сокращения Ежегодная рента - актив, который платит установленную сумму в каждом Сокращение расчёта ежегодной рентыПример Вы соглашаетесь арендовать автомобиль в течение 4 Сокращение расчёта ежегодной рентыПример Вы соглашаетесь арендовать автомобиль в течение 4 Сложный процент Сложный процент ИнфляцияИнфляция - величина на которую цены в целом увеличиваются.Норма номинальной ставки процента ИнфляцияФормула приближенияреальная процентная ставка   Номинальная процентная ставка - уровень инфляции ИнфляцияПример Если процентная ставка государственных облигаций со сроком один год - 5.9 %, ИнфляцияПример Если процентная ставка государственных облигаций со сроком один год - 5.9 %, ИнфляцияПример Если процентная ставка государственных облигаций со сроком один год - 5.9 %, Оценка облигацийПример Если сегодня - октябрь 2000, что является стоимостью следующих облигаций? Оценка облигацийПример Если сегодня - октябрь 2000, что является стоимостью следующих облигаций? Цены облигаций и доходыЦеныдоходы
Слайды презентации

Слайд 2 Содержание
Оценка долгосрочных активов
Сокращения при расчете PV
Сложный процент
Процентные ставки

СодержаниеОценка долгосрочных активовСокращения при расчете PVСложный процентПроцентные ставки и инфляцияПример : Текущая стоимость и облигации

и инфляция
Пример : Текущая стоимость и облигации

Слайд 3 Текущая стоимость
Коэфф. дисконтирования =
= DF = PV для

Текущая стоимостьКоэфф. дисконтирования == DF = PV для $1Коэффициенты дисконтирования могут

$1



Коэффициенты дисконтирования могут использоваться, чтобы вычислить текущую стоимость любого

потока наличности.

Слайд 4 Текущая стоимость






Коэффициенты дисконтирования могут использоваться, чтобы

Текущая стоимость Коэффициенты дисконтирования могут использоваться, чтобы вычислить текущую стоимость любого потока наличности.

вычислить текущую стоимость любого потока наличности.

Слайд 5 Текущая стоимость








Замена “1”

Текущая стоимость Замена “1” с “t” позволяет использовать формулу

с “t” позволяет использовать формулу для денежных потоков, которые

существуют в любой точке времени.

Слайд 6 Текущая стоимость
Пример
Вы только что купили новый компьютер

Текущая стоимостьПример Вы только что купили новый компьютер за $ 3,000.

за $ 3,000. Условия платежа - 2 года, так

же как и за наличный расчет. Если Вы можете заработать 8 % на ваших деньгах, сколько денег Вы должны отложить, сегодня чтобы произвести оплату в срок через два года?

Слайд 7 Текущая стоимость
Пример
Вы толькочто купили новый компьютер за

Текущая стоимостьПример Вы толькочто купили новый компьютер за $ 3,000. Условия

$ 3,000. Условия платежа - 2 года так же

как и за наличный расчет. Если Вы можете заработать 8 % на ваших деньгах, сколько денег Вы должны отложить, сегодня чтобы произвести оплату в срок через два года?

Слайд 8 Текущая стоимость
PVS можно складывать, чтобы оценить

Текущая стоимость PVS можно складывать, чтобы оценить многократные потоки наличности.

многократные потоки наличности.

Слайд 9 Текущая стоимость
Учитывая два доллара, один получил за год

Текущая стоимостьУчитывая два доллара, один получил за год с этого времени

с этого времени и другой за два года с

этого времени, величину обычно называемую Коэффициентом дисконтирования.

Примем r1 = 20 % и r2 = 7 %.

Слайд 10 Текущая стоимость
Учитывая два доллара, один получил за год

Текущая стоимостьУчитывая два доллара, один получил за год с этого времени

с этого времени и другой за два года с

этого времени, величину обычно называемую Коэффициентом дисконтирования. Примем r1 = 20 % и r2 = 7 %.

Слайд 11 Текущая стоимость
Пример
Предположим, что потоки наличности от

Текущая стоимость Пример Предположим, что потоки наличности от строительства и продажи здания

строительства и продажи здания офиса следующие. С учётом 7

% требуемой ставки дохода, создается ориентировочная текущая стоимость и показывается чистая приведенная стоимость.

Слайд 12 Текущая стоимость
Пример - продолжение
Предположим, что потоки наличности

Текущая стоимостьПример - продолжение Предположим, что потоки наличности от строительства и

от строительства и продажи здания офиса следующие. С учётом

7 % требуемой ставки дохода, создается ориентировочнаятекущая стоимость и показывается чистая приведённая стоимость.

Слайд 13 Сокращения
Имеются сокращения, которые облегчают вычисление текущей стоимости актива,

СокращенияИмеются сокращения, которые облегчают вычисление текущей стоимости актива, который выплачивается в

который выплачивается в различных периодах. Эти сокращения позволяют нам

быстро производить вычисления.

Слайд 14 Сокращения
Пожизненная рента- Финансовая концепция, в которой

Сокращения Пожизненная рента- Финансовая концепция, в которой поток наличности теоретически получен навсегда.

поток наличности теоретически получен навсегда.

Слайд 15 Сокращения
Пожизненная рента - Финансовая концепция, в

Сокращения Пожизненная рента - Финансовая концепция, в которой поток наличности теоретически получен навсегда.

которой поток наличности теоретически получен навсегда.

Слайд 16 Сокращения
Ежегодная рента - актив, который платит

Сокращения Ежегодная рента - актив, который платит установленную сумму в каждом году за указанное число лет.

установленную сумму в каждом году за указанное число лет.

Слайд 17 Сокращение расчёта ежегодной ренты
Пример
Вы соглашаетесь арендовать автомобиль

Сокращение расчёта ежегодной рентыПример Вы соглашаетесь арендовать автомобиль в течение 4

в течение 4 лет за $ 300 в месяц.

От вас не требуется оплаты вначале или в конце вашего соглашения. Если ваша возможная цена капитала - 0.5 % в месяц, что является стоимостью арендного договора?

Слайд 18 Сокращение расчёта ежегодной ренты
Пример
Вы соглашаетесь арендовать автомобиль

Сокращение расчёта ежегодной рентыПример Вы соглашаетесь арендовать автомобиль в течение 4

в течение 4 лет за $ 300 в месяц.

От вас не требуется оплаты вначале или в конце вашего соглашения. Если ваша возможная цена капитала - 0.5 % в месяц, что является стоимостью арендного договора?

Слайд 19 Сложный процент

Сложный процент

Слайд 20 Сложный процент

Сложный процент

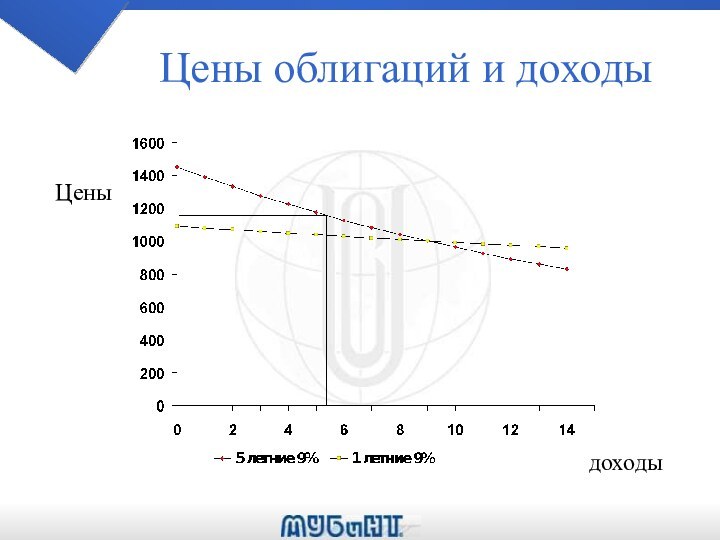
Слайд 21 Инфляция
Инфляция - величина на которую цены в целом

ИнфляцияИнфляция - величина на которую цены в целом увеличиваются.Норма номинальной ставки

увеличиваются.
Норма номинальной ставки процента - величина, на которую вложенные

деньги растут.
Реальная процентная ставка - величина на которую увеличивается покупательная способность инвестиций.

Слайд 22 Инфляция
Формула приближения
реальная процентная ставка 
 Номинальная процентная

ИнфляцияФормула приближенияреальная процентная ставка   Номинальная процентная ставка - уровень инфляции

ставка - уровень инфляции

Слайд 23 Инфляция
Пример
Если процентная ставка государственных облигаций со сроком один

ИнфляцияПример Если процентная ставка государственных облигаций со сроком один год - 5.9

год - 5.9 %, и рост инфляции - 3.3

%, что является реальной процентной ставкой ?

Слайд 24 Инфляция
Пример
Если процентная ставка государственных облигаций со сроком один

ИнфляцияПример Если процентная ставка государственных облигаций со сроком один год - 5.9

год - 5.9 %, и рост инфляции - 3.3

%, что является реальной процентной ставкой ?

Слайд 25 Инфляция
Пример
Если процентная ставка государственных облигаций со сроком один

ИнфляцияПример Если процентная ставка государственных облигаций со сроком один год - 5.9

год - 5.9 %, и рост инфляции - 3.3

%, что является реальной процентной ставкой ?

Слайд 26 Оценка облигаций
Пример
Если сегодня - октябрь 2000, что является

Оценка облигацийПример Если сегодня - октябрь 2000, что является стоимостью следующих облигаций?

стоимостью следующих облигаций?
IBM по облигациям платит

$ 115 каждый сентябрь в течение 5 лет. В сентябре 2005 доплачивает дополнительно $ 1000 и гасит облигации. Облигации оценены, AAA (WSJ AAA YTM - 7.5 %).

Слайд 27 Оценка облигаций
Пример
Если сегодня - октябрь 2000, что является

Оценка облигацийПример Если сегодня - октябрь 2000, что является стоимостью следующих облигаций?

стоимостью следующих облигаций?
IBM по облигациям платит

$ 115 каждый сентябрь в течение 5 лет. В сентябре 2005 доплачивает дополнительно $ 1000 и гасит облигации. Облигации оценены, AAA (WSJ AAA YTM - 7.5 %).

  • Имя файла: kak-vychislyat-tekushchuyu-stoimost.pptx
  • Количество просмотров: 140
  • Количество скачиваний: 0
- Предыдущая Маркетинговаінформаційнасистема
Следующая - Армия Крайова

Похожие презентации

Мониторинг социальных медиа Мониторинг социальных медиа 179
БИЗНЕС ПЛАН - ОСНОВА СОЗДАНИЯ ФИРМЫ БИЗНЕС ПЛАН - ОСНОВА СОЗДАНИЯ ФИРМЫ 168
Денежный рынок: спрос, предложение, равновесие Денежный рынок: спрос, предложение, равновесие 141
Экономика труда, как наука. Содержание, структура Экономика труда, как наука. Содержание, структура 127
Северо-западный экономический регион Северо-западный экономический регион 117
Государство в эпоху глобализации: геополитика и геоэкономика Государство в эпоху глобализации: геополитика и геоэкономика 135
Запасы. Оценка запасов. МСФО (IAS) 2 Запасы. Оценка запасов. МСФО (IAS) 2 160
Экономическая эффективность отрасль растениеводства в целом в млн. рублях Экономическая эффективность отрасль растениеводства в целом в млн. рублях 121
Теория экономического анализа Теория экономического анализа 144
Население. Безработица.Гендерный баланс Население. Безработица.Гендерный баланс 114
Экономические связи Архангельской области Экономические связи Архангельской области 135
Планирование товарного ассортимента в системе маркетинга Планирование товарного ассортимента в системе маркетинга 192
Оффшорные компании Оффшорные компании 142
Проблемы кредитования малого предпринимательства Проблемы кредитования малого предпринимательства 46
Основы теории спроса и предложения Основы теории спроса и предложения 117
Тема 12. Карточные платежные системы Тема 12. Карточные платежные системы 143
Монополия и антимонопольное регулирование Монополия и антимонопольное регулирование 151
1С:Бухгалтерия строительной организацией 2.0 1С:Бухгалтерия строительной организацией 2.0 113
Бухгалтерская отчетность Бухгалтерская отчетность 151
Мероприятия по повышению устойчивости функционирования объектов экономики в ЧС Мероприятия по повышению устойчивости функционирования объектов экономики в ЧС 133
Система бюджетирования Система бюджетирования 159
Основы макроэкономического анализа Основы макроэкономического анализа 171
Оформление организационных документов Оформление организационных документов 138
Капiтал i наймана праця Капiтал i наймана праця 133
Маркетинг персонала Маркетинг персонала 112
Эффект масштаба Эффект масштаба 158
Социология экономики и труда (тема №13 ) Социология экономики и труда (тема №13 ) 138
Облік валютних операцій (3.1 - 3.3) Облік валютних операцій (3.1 - 3.3) 105
Сущность системы управления производственными запасами предприятия-участника ВЭД Сущность системы управления производственными запасами предприятия-участника ВЭД 91
Затраты на производство Затраты на производство 101