Презентация на тему Облигации. Основные понятия и параметры облигации

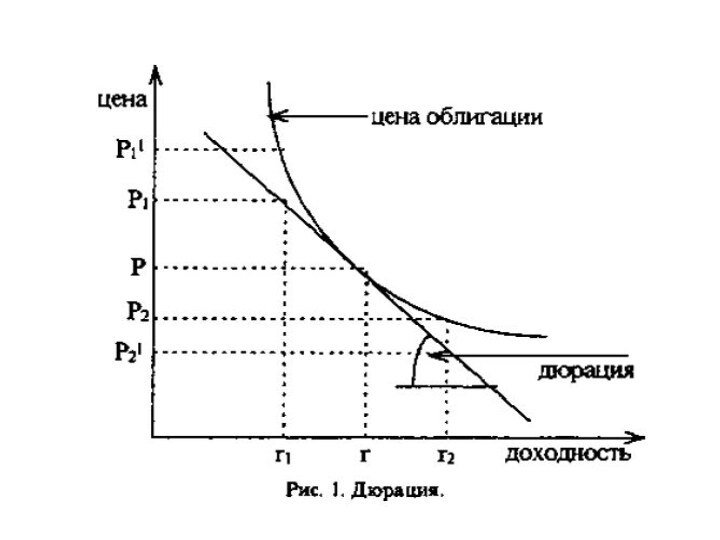
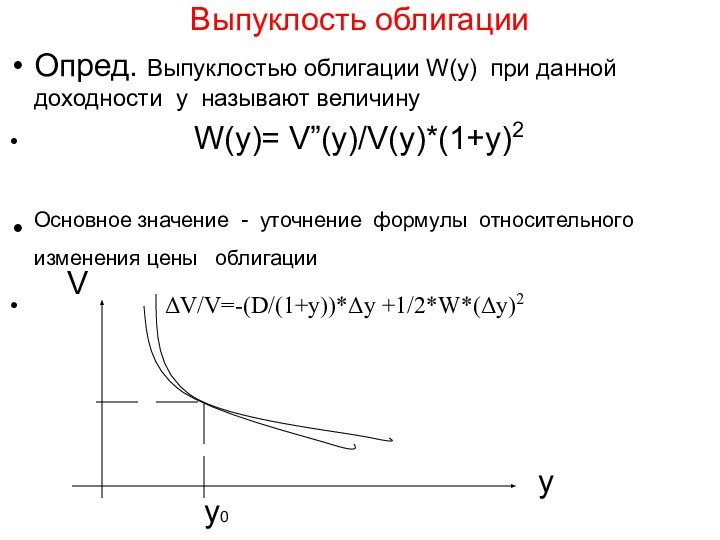
бумага , длительный заем эмитенту от ее обладателя и

оговоренный доход обладателю. Он обычно ниже , чем от других ЦБ, но более надежен и стабилен. В облигации чаще всего инвестируют свободные средства пенсионные фонды, ПИФЫ и др.
ПАРАМЕТРЫ ОБЛИГАЦИИ.
Дата погашения (Т- время обращения ОБ с момента выпуска);
Срок погашения (n=T- t , где t -текущее время).
НОМИНАЛЬНАЯ СТОИМОСТЬ (N) –сумма денег , выплачиваемая владельцу облигации на дату погашения. Обычно указывается на самой облигации.
Выкупная стоимость ( если она отличается от номинальной).

выплачиваются владельцу ежегодно по купонной ставке – с (норма

дохода)-с = С/N.
Опр. Если выплаты по купонам не предусмотрены , то такую облигацию называют безкупонной. Доход по ней образуется за счет курсовой разницы стоимости облигации.

краткосрочные (от года до 3 лет), среднесрочные (от 3

до 7 лет), долгосрочные (от 7 до 30 лет) и бессрочные (выплаты процентов осуществляются неопределённо долго).

- С. Поэтому в момент времени t вводится понятие

текущей стоимости - Р облигации ( r- процентная ставка, n-время до погашения)



Так как С=сN,то

руб., сроком погашения n= 5 лет и ежегодными выплатами.

По купонной ставке c=15% при годовой процентной ставке r= 20%.

Решение. Подставляя в формулу (О1) получим

есть отношение вида: K=V/N*100%,

где V-рыночная (курсовая) цена облигации определяется конъюнктурой рынка. .
Текущая доходность – i=C/V=cN/V=c/K.

то ее курсовая стоимость равна

K=V/N*100%=90% т.е. курс облигации составляет 90 % от номинала.

где ρ - доходность к погашению
Если С=сN,то

Решение при n<10

(О2)

V>N ( K >1) ρ

<=> ρ>c,

сроком погашения, но с различной структурой купонных платежей, необходимо

учитывать особенности распределения доходов во времени («профиль»поступления доходов).
Также важно знать как реагирует цена или стоимость на изменение процентной ставки.

P(y)=ΣСk(1+y)-tk .

Продиф. функцию P(y) по y и разделим на P:
P`(y)/P(y)=- [1/(1+y)] *Σwk*tk, (О3)

D= Σwk*tk

где wk= Ck(1+y)-tk / P(y)– весовые коэфф. определяющ. вклад каждого платежа - Ck(1+y)-tk в текущ. стоим. всего потока - P(y) и
Σ wk =1

время всех выплат. Так дюрация бескупонной облигации равна сроку

n до ее погашения. В остальных случаях D

дюрацию облигаций MD



Отсюда получим, при малых процентных изменениях

MD показывает на сколько процентов уменьшится облигация при увеличении

средней доходности по рынку на 1%. Так при увеличении доходности на 1% , т.е. при Δ=1% получаем , что ΔP/P=-MD

y называют величину

W(y)= V”(y)/V(y)*(1+y)2

Основное значение - уточнение формулы относительного изменения цены облигации
ΔV/V=-(D/(1+y))*Δy +1/2*W*(Δy)2

у

V

у0