Слайд 2
Полезность семи конфет равна 40, а полезность восьми
конфет равна 44. определите предельную полезность седьмой, восьмой и
девятой конфеты
Слайд 3
Первое яблоко доставляет Ивану удовлетворение, равное 8. Каждое
следующее яблоко доставляет добавочное удовлетворение, на 2 меньше предыдущего.
Начиная с какого яблока суммарное удовлетворение от потребления яблок будет уменьшаться?
Слайд 4
Равновесный объем продуктов состоит из нескольких стаканов молока
и нескольких кусков хлеба. Если в него добавить один
стакан молока, то полезность набора увеличится на 12 единциц, а если добавить один кусок хлеба, то на 8 единиц. Цена стакана молока равна 9 руб. Найдите цену куска хлеба
Слайд 5
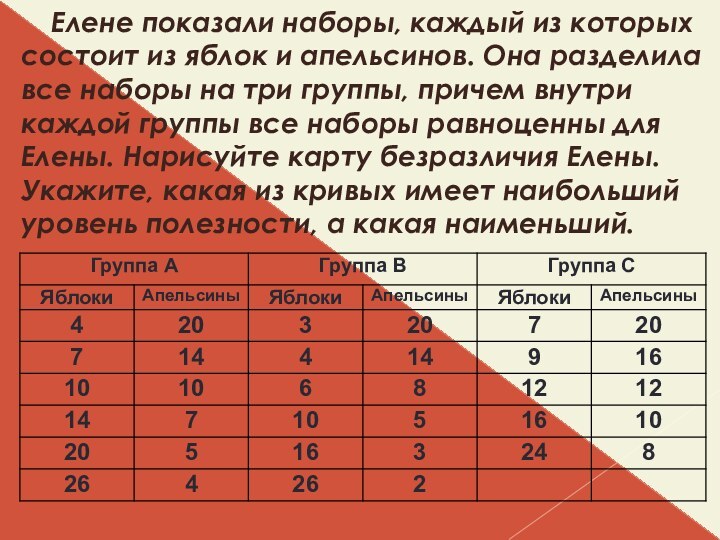
Елене показали наборы, каждый из которых состоит из
яблок и апельсинов. Она разделила все наборы на три
группы, причем внутри каждой группы все наборы равноценны для Елены. Нарисуйте карту безразличия Елены. Укажите, какая из кривых имеет наибольший уровень полезности, а какая наименьший.
Слайд 6
Доход 200 руб. в неделю индивид тратит на
покупку двух товаров по ценам Рх = 5 руб.
и Ру = 10 руб. Нарисуйте бюджетную линию. Как изменится бюджетная линия при росте доходов до 240 руб.? Как пройдет бюджетная линия при доходе 200 и ценах Рх = 2,5 руб. и Ру = 4 руб.?
Слайд 7
Бюджетное ограничение задано формулой 8х+6у=20. Найдите максимально возможный
объем потребления продукта Х.
Слайд 8
Студент еженедельно получает от родителей 800 рублей на
карманные расходы. Начертите бюджетную линию студента для каждой из
ситуаций, обозначив продукты питания по оси ординат, а развлечения – по оси абсцисс:
1) цена продуктов питания Рп = 20 рублей за единицу; цена развлечений Рр = 20 рублей за единицу; 2) Рп = 20 рублей за единицу; Рр = 40 рублей за единицу; 3) Рп = 40 рублей за единицу; Рр = 20 рублей за единицу; 4) Рп = 16 рублей за единицу; Рр = 16 рублей за единицу; 5) Рп = 20 рублей за единицу; Рр = 20 рублей за единицу, но доходы студента увеличиваются до 1000 рублей в неделю. Прокомментируйте бюджетные линии 4) и 5) и сравните их с бюджетной линией 1).
Слайд 9
Индивид тратит весь доход либо на 8 единиц
блага Х и 18 единиц блага У, либо на
12 единиц блага Х и 10 единиц У. Сколько единиц У сможет он купить, если вообще откажется от блага Х?
Слайд 10
Иван обычно на свой доход покупал 300 единиц
товара Х и 150 единиц товара У при ценах
Рх = 6 и Ру = 12. Если цены изменятся до уровня Рх = 15 и Ру =24, то на сколько должен возрасти доход, чтобы он мог позволить себе тот же набор?
Слайд 11
У всех покупателей на рынке стамесок наблюдается одинаковая
функция индивидуального спроса Q = 8 – 0,5P. Определите
функцию рыночного спроса, если покупателей на рынке 20 человек.
Слайд 12
Петр покупает 30 роз в месяц по цене,
меньшей 40 руб., и не покупает вовсе при больших
ценах. Иван покупает 40 роз в месяц при цене, меньшей 30 руб., и не покупает вовсе при больших ценах. Постройте график суммарного спроса на розы.
Слайд 13
Функция спроса Ивана Q = 6 – 3P,
функция спроса Марии Q = 4 – 0,5P. Постройте
кривую суммарного спроса.
Слайд 14
Индивидуальный спрос трех покупателей: Алексея, Виктора и Сергея
на шурупы задан следующими функциями:
QА = 24 –
6Р; QВ = 32 – 8Р;
QС = 44 – 11 Р.
Определите рыночный спрос трех покупателей и представьте его графически.
Слайд 15
Известны коэффициенты эластичности спроса на товар Х: по
цене самого товара Ех = – 2, по цене
товара-конкурента Еху =+1,5, по доходу ЕI = +2. Как изменится в процентном отношении спрос на товар при 1) увеличении цены самого товара на 5%, 2) уменьшении цены товара-конкурента на 6%, 3) увеличении дохода потребителя на 3%?
Слайд 16
При увеличении цены масла на 2% спрос на
него сократился на 3%, а спрос на финское масло
увеличился на 2,5%. Найдите эластичность спроса на масло и перекрестную эластичность спроса на маргарин.
Слайд 17
В результате повышения цены с 5 до 6
рублей объем спроса сократился с 9 до 7 млн.
штук в год. Определите коэффициент прямой эластичности.