Слайд 2
РЫНОК БЛАГ
Потребительский спрос
Инвестиционный спрос
Спрос государства
Спрос заграницы
Слайд 3
Факторы:
- доход на факторы производства;
- налоги
и трансферты, рост отчислений на социальное и медицинское страхование;
-
размер имущества, богатства;
- уровень дифференциации населения по уровню доходов и размеров имущества;
- численность и возрастная структура населения,
- ожидания населения;
- размер потребительской задолженности,
- уровень цен.
Потребительский спрос
Слайд 4
Гипотеза абсолютного дохода
Yd = С + S
Yd = Y – Т
Где
Yd - располагаемый доход
Y
— личный доход
С - потреблению
S - сбережения
Т — налоги
Слайд 5
«Основной психологический закон, состоит в том, что люди
склонны, как правило, увеличивать свое потребление с ростом дохода,
но не в той же мере, в какой растет доход».
Слайд 6
МРС = ΔC / ΔYd, где
ΔС
- изменение потребления;
Δ Yd – изменение располагаемого дохода.
МРС -
предельная склонность к потреблению показывает, какую долю дополнительного дохода потребитель склонен потратить на потребление.
Слайд 7
МРS = ΔS /ΔYd , где
ΔS - изменение
сбережений;
Δ Yd - изменение располагаемого дохода
МРS -
предельная склонность к сбережению, которая показывает, какую долю дополнительного дохода потребители склонны сберегать
Слайд 8
Кейнсианская функция потребления
С = a + b
* Yd; а > 0; 0 < b
< 1,
где С — функция потребления;
a — автономное потребление, не зависящее от дохода
b — предельная склонность к потреблению (МРС);
Yd -располагаемый доход (Y-T)
Слайд 9
Налоговая функция
Т = Тa + t * Y,
где:
Т — налоговая функция;
Тa — автономные налоги, не
зависящие от уровня дохода;
t — ставка налогообложения.
Если Тa = 0, то Т = t * Y
Слайд 10
Располагаемый доход:
Yd = Y-t*Y = Y(1-t),
Кейнсианская функция
потребления:
С = а + b(1-t)Y
Слайд 11
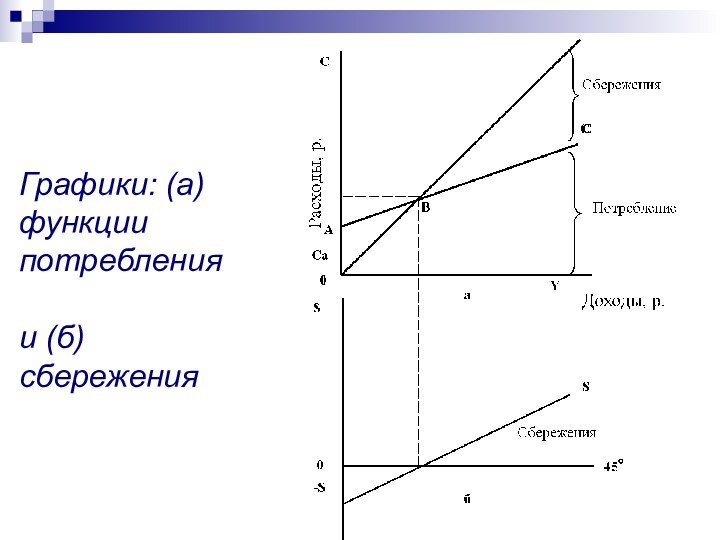
Графики: (а) функции потребления
и (б) сбережения
Слайд 12
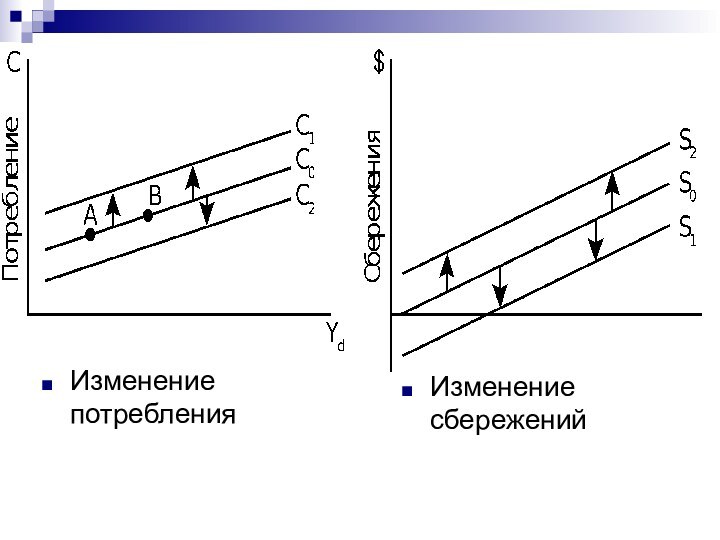
Изменение потребления
Изменение сбережений
Слайд 13
«Загадка Кузнеца»
С. Кузнец, основываясь на результатах исследований
экономики США показал, что в долгом периоде снижение средней
нормы потребления не происходит:
1869-1898 гг. С/у = 0.867;
1884-1913 гг. С/у= 0.867;
1904-1930 гг.- С/у= 0.879.
Слайд 14
Гипотеза относительного дохода
C*/ yi = α0 + α1
y*/yi; α0> 0; α1> 0;
С* - потребление отдельного
домашнего хозяйства;
yi - средний доход социального слоя, к которому принадлежит данное домашнее хозяйство, или индивид.
y* - абсолютный доход индивида.
Слайд 15
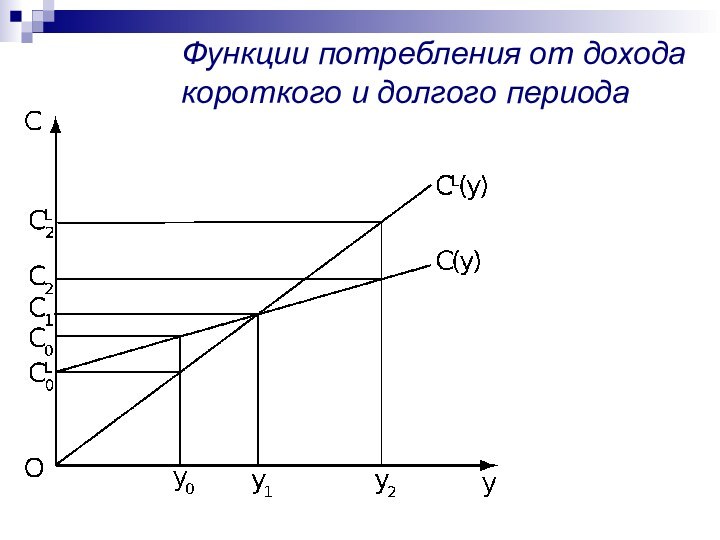
Функции потребления от дохода
короткого и долгого периода
Слайд 16
Функция потребления в теории постоянного дохода Милтона Фридмана
Y = Yp + Yt ,
где Y -
Текущий доход;
Yp : постоянный доход
Yt : временный доход
Слайд 17
Средняя склонность к потреблению
APC = C/Y = αYp/Y
С=αYp
Функция потребления в теории постоянного дохода
Слайд 18
С = (W + ТnY)/T о
где W
- начальное богатство;
Y – ожидаемый среднегодовой заработок за весь
период работы,
То – ожидаемое число лет жизни после вступления в трудовую деятельность (время работы и пребывания на пенсии)
Тn - планируемое число лет работы
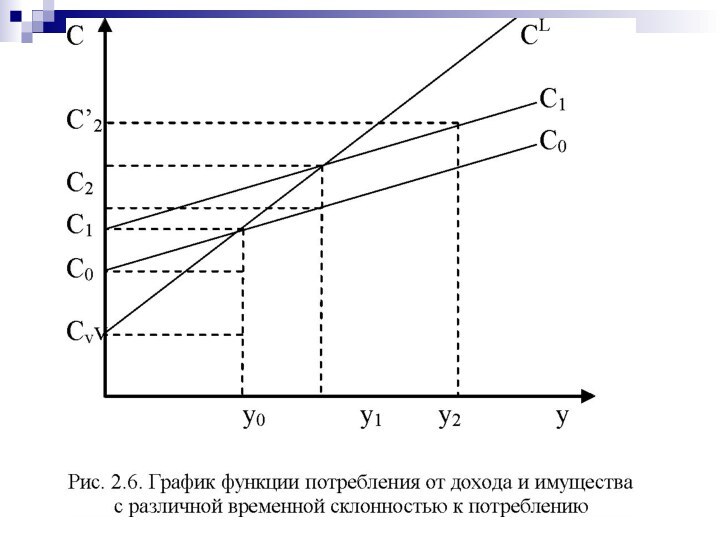
Функция потребления в модели «жизненного цикла» Ф. Модильяни
Слайд 19
C = (1/Tо)W + (Тn/Tо)Y
Потребление зависит как
от уровня дохода, так и от размера первоначального богатства
C = bwW + bY
где bw=-(1/Tо) - предельная склонность к потреблению по накопленному богатству (имуществу) W, она показывает, на сколько изменится потребление, если имущество изменится на единицу,
by = Тn/Tо -предельная склонность к потреблению по доходу Y показывает, на сколько изменится потребление, если доход (зарплата) изменится на единицу.
Слайд 20
Современная модификация кейнсианской функции потребления
Ct = byt
+b(1 - θ)yt-1+ bwW
где
Сt — функция потребления
в текущем году;
b — предельная склонность к потреблению (МРС);
yt – доход в текущем году
yt-1 доход в предыдущем году
Θ –доля постоянного дохода
Слайд 22
Неоклассические функции потребления
Слайд 23
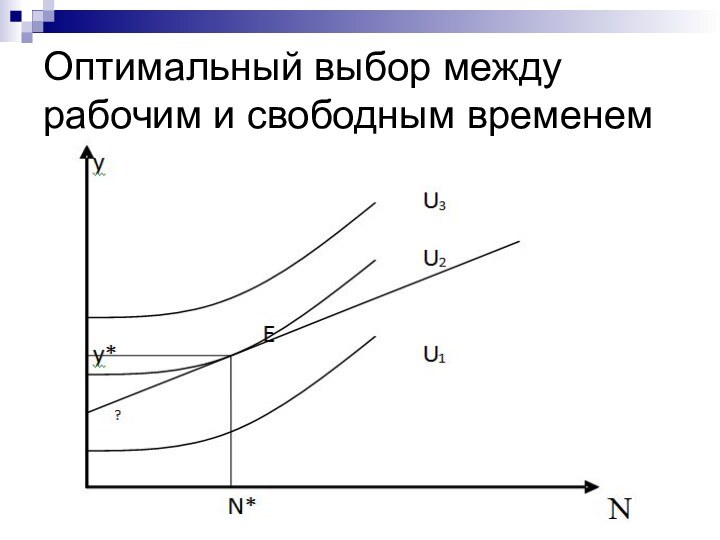
Оптимальный выбор между рабочим и свободным временем
Слайд 24
функция полезности: U= (yH)0,5
бюджетное ограничение у =
wN + W
Где w-часовая ставка з/п
N-рабочее время (N=T-H)
H-свободное
время
W-имущество
Составим функцию Лагранжа:
L=(yH)0,5 + λ(w (T-H) +W -у)
Она достигает максимума при:
δLag /δy =( 0.5U / y) – λ = 0
δLag / δH =( 0.5U / H) – λw = 0
δLag /δ λ = w ( T - H) + W - y = 0
wH = 0;
2w N = wT – W;
N* =
(T / 2) – (W / 2w )
Оптимальное количество рабочего времени (N*)
Слайд 26
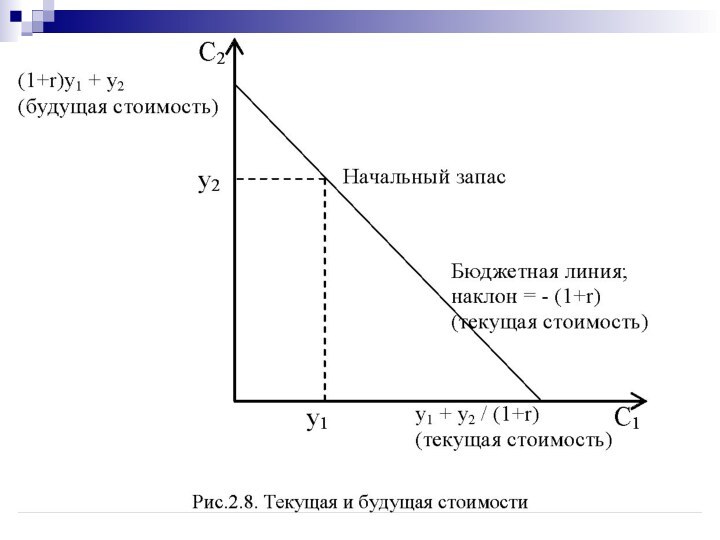
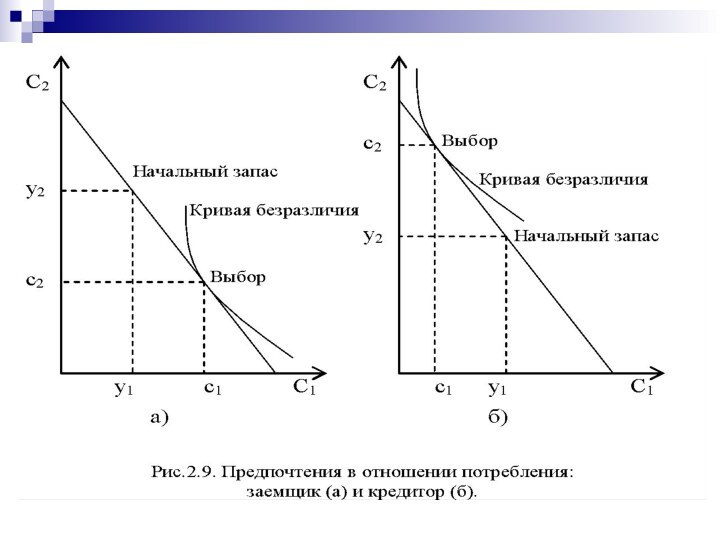
уравнение бюджетного ограничения
Межвременное бюджетное ограничение
Слайд 29
Инвестиционный спрос
Кейнсианская функция автономных инвестиций:
I=Ii(R*-i)
Где I
– инвестиции
Ii - предельная склонность к инвестициям (ΔI/ΔY)
R*- внутренняя
норма доходности проекта
i – рыночная ставка процента
Слайд 30
Реальный доход от передачи в аренду единицы капитала
равен его реальной цене .
Реальная цена совпадает с
предельной производительностью капитала МРК.
Неоклассическая модель инвестиций
Слайд 31
Реальная арендная цена капитала увеличивается, если:
запас капитала уменьшается,
увеличивается
объема используемого труда;
совершенствуется технологии.
Слайд 32
Затраты при предоставлении в аренду капитала:
-Альтернативные издержки
Pk -
цена приобретения единицы капитала
i - номинальная ставка процента
iPK - это сумма, которую фирма получила бы, если вместо покупки единицы оборудования поместила бы данную сумму в банк
- Издержки от изменения цены капитала за время сдачи его в аренду – (∆Pk).
- Издержки от износа δРk (δ-норма амортизации)
Слайд 33
Суммарные издержки от сдачи единицы капитала в аренду,
складываются из трех вышеперечисленных видов затрат и составляют:
iPk -∆
Pk + δРk = Рk ( i - ∆ Pk / Рk +δ),
где ∆ Pk / Рk – темп инфляции инвестиционных товаров.
Слайд 34
Если темп инфляции инвестиционных товаров совпадает с темпом
инфляции остальных товаров, то есть
∆ Pk / Рk
= π .
Тогда издержки на единицу капитала
Рk (i- π+ δ) = Рk (r+ δ).
Слайд 35
Реальная прибыль на единицу капитала, предоставленного в аренду
(норма прибыли) составит:
Слайд 36
Предприятию следует:
инвестировать, если норма прибыли положительна, то есть
сокращать запас капитала, если
Слайд 37
Чистые инвестиции зависят от нормы прибыли
Слайд 38
Чистые инвестиции предприятия:
растут, т.е. ∆К >
0), если
снижаются, т.е. ∆К< 0, если
Слайд 39
Инвестиции в основные фонды предприятий:
условие достижения устойчивого состояния
запаса капитала:
MPK = (r +δ)
Слайд 40
Издержки по вводу инвестиций:
С2(К1+1 – Кt)2, при
С1, С2 > 0
Суммарные издержки фирмы:
С1(К* -
Кt+1)2 + С2(К1+1 – Кt)2
Слайд 41
Фирма будет минимизировать издержки:
С1(К* - Кt+1) 2 +
С2(Кt+1 – Кt)2 → min
Отсюда следует, что
Кt+1 –
Кt =
К* - устойчивое состояние запаса капитала, то скорость движения к этому состоянию зависит от коэффициента
Слайд 42
Если С1 велико по сравнению C2, то устойчивое
состояние будет достигнуто очень быстро.
Если С2 сравнительно велико,
то процесс установления равновесного состояния будет медленным.
Слайд 43
Коэффициент Тобина q :
q = Рыночная стоимость установленного
капитала / Восстановительная стоимость установленного капитала
Слайд 44
если q > 1, то рыночная стоимость акций
компании больше стоимости замещения капитала, следовательно, выгодно наращивать капитал.
-
если q < 1, то, наоборот, фирмы не будут замещать капитал по мере его выбытия.
- если прибыль фирм от владения капиталом положительна, МРК > (r + δ), то владение этими фирмами выгодно и это повышает рыночную стоимость их акций, а, следовательно, и q Тобина.
- если прибыль отрицательна, то q падает
Слайд 45
Если предположить, что чистая прибыль от единицы установленного
капитала (МРК - δ) не меняется во времени, то
Слайд 46
При q > 1, МРК > (r +δ)
и, согласно неоклассической теории инвестиций, фирмы будут инвестировать.
При
q < 1, МРК<(r + δ) и фирмы не будут возмещать выбывший капитал.
Слайд 47
Чистые частные инвестиции включают в себя также инвестиции
в жилищное строительство и инвестиции в запасы
Инвестиции в жилищное
строительство зависят от спроса на жилье. Функция спроса на жилье зависит от относительной цены жилья (Pн/P).
Издержки строительных фирм зависят от общего уровня цен Р, а доходы – от цены жилья Рн.
Слайд 48
Итоговую функцию инвестиций, можно представить как:
I=e-dR
где
R –ставка процента,
е - эмпирическая коэффициент.
Слайд 49
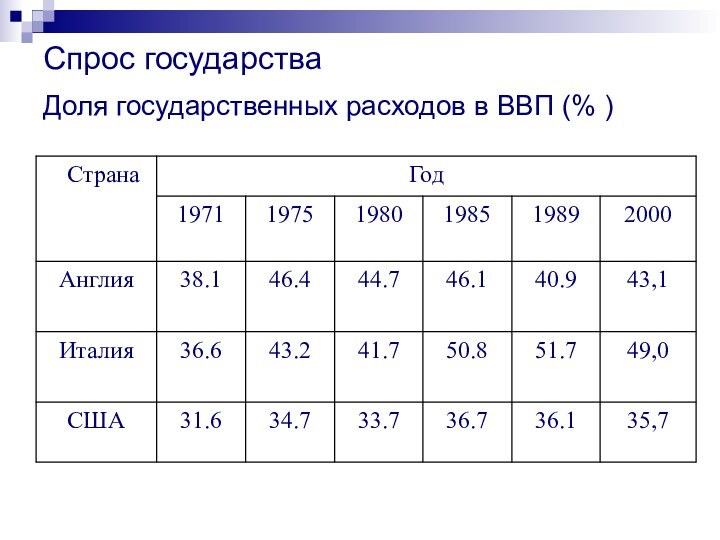
Спрос государства
Доля государственных расходов в ВВП (% )
Слайд 50
θ=Р/ еPz
где Р, P z — уровни цен
соответственно внутри страны и за границей;
е — обменный
курс отечественной валюты, показывающий, сколько единиц отечественной валюты дают за единицу иностранной валюты.
Спрос заграницы
Слайд 51
Функция чистого экспорта NХ:
NХ=g-m’Y-nR,
где g — величина автономного
экспорта,
m’ — предельная склонность к импортированию;
n – чувствительность
чистого экспорта к ставке процента
R – ставка процента.
Слайд 52
Кейнсианская
yD = C(y) + I(R*, i)+G + NХ(θ,
у)
Неоклассическая
yD = C(i) + I(r, i)+G + NХ(θ, у)