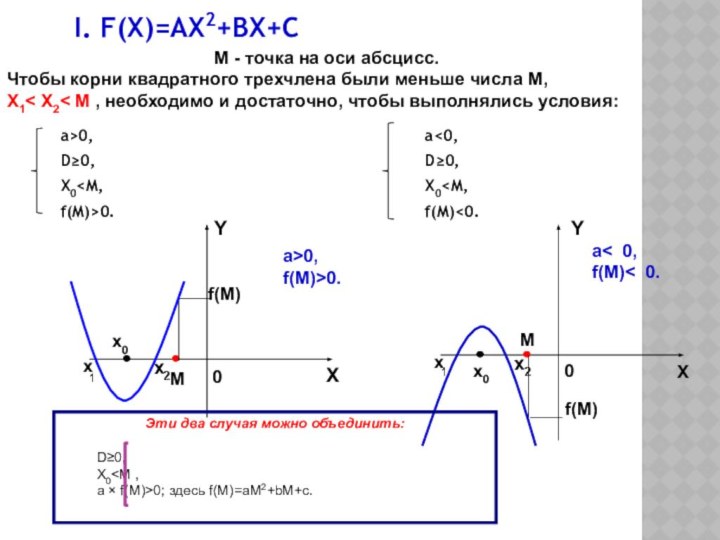
корни квадратного трехчлена были меньше числа М,
Х1< X2< М
, необходимо и достаточно, чтобы выполнялись условия:0
0
a< 0,
f(M)< 0.
a>0,
f(M)>0.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть
















0
0
a< 0,
f(M)< 0.
a>0,
f(M)>0.
M
Y
x
1
x2
x0
f(M)
X
M
Y
x
1
x2
x0
f(M)
X
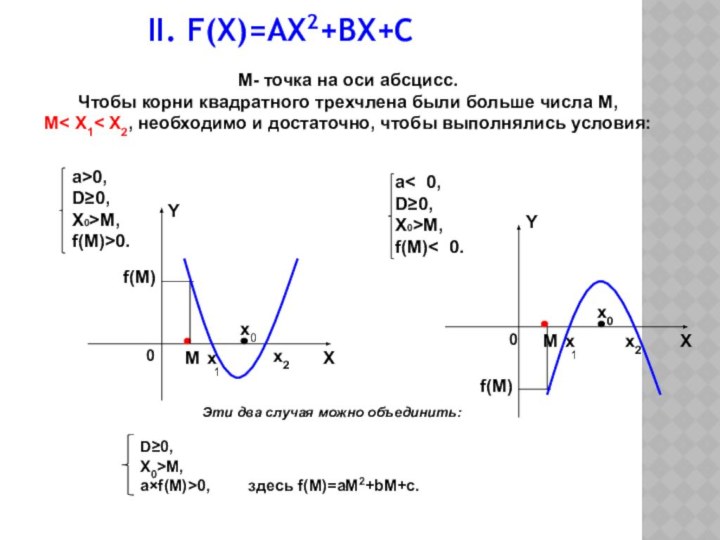
a< 0,
D≥0,
X0>M,
f(M)< 0.
a>0,
D≥0,
X0>M,
f(M)>0.
Эти два случая можно объединить:
D≥0,
X0>M,
a×f(M)>0, здесь f(M)=aM2+bM+c.
0
0
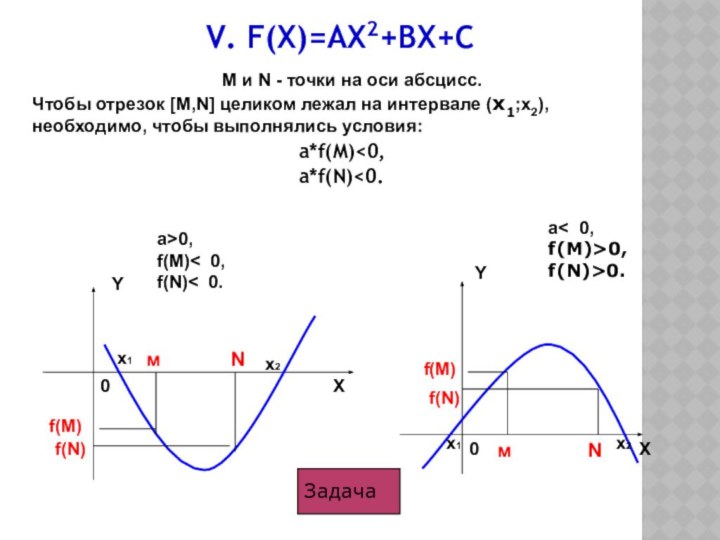
II. F(X)=AX2+BX+C
X
Y
м
м
о
f(M)
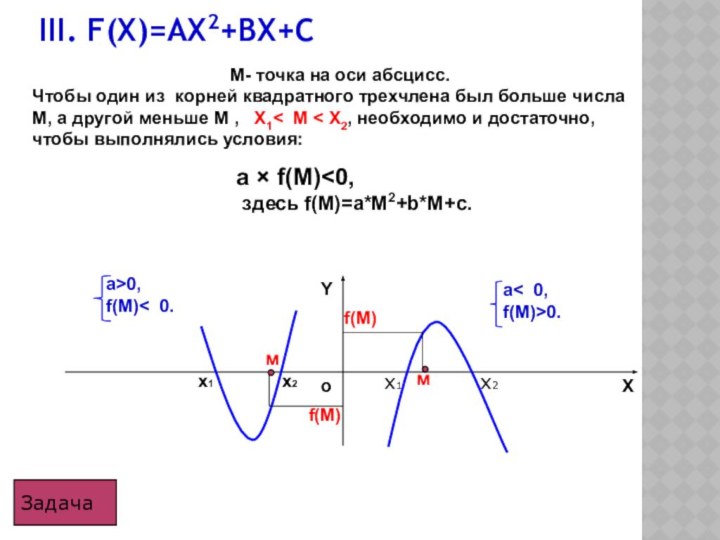
a>0,
f(M)< 0.
a< 0, f(M)>0.
f(M)
x1
x2
х1
х2
III. F(X)=AX2+BX+C
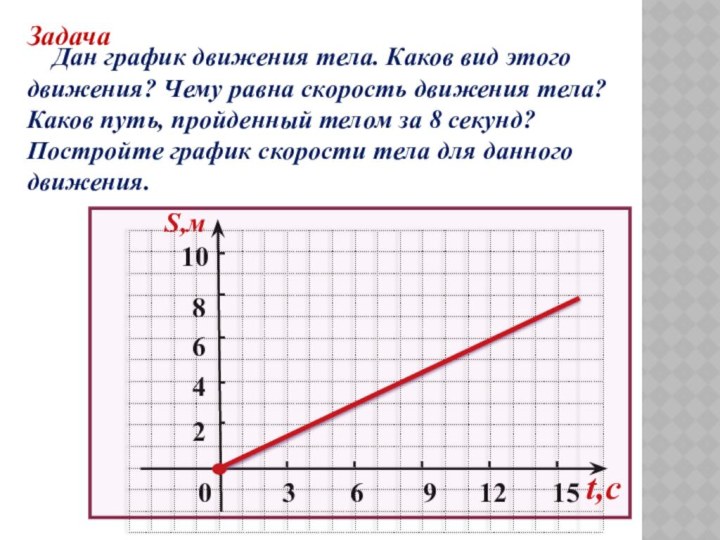
Задача
м
м
x1
x2
x2
x1
N
N
x0
x0
f(N)
f(M)
f(M)
f(N)
Задача
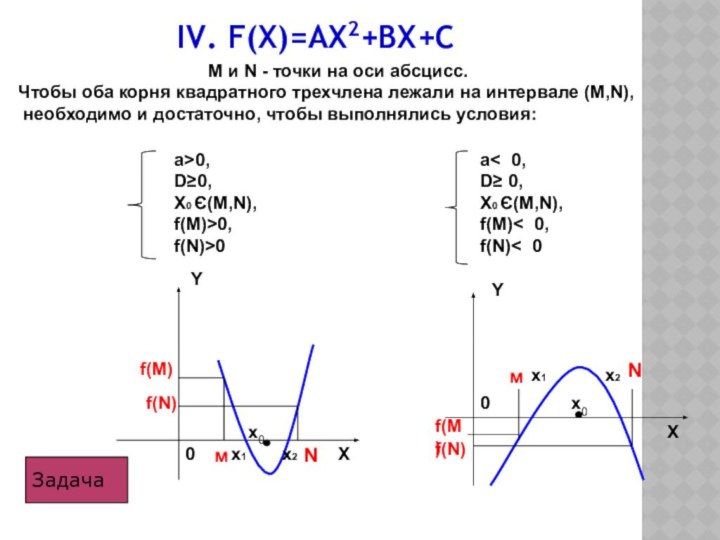
a>0,
f(M)< 0,
f(N)< 0.
a< 0,
f(M)>0,
f(N)>0.
Задача
-3/4
0
а
+
-
+
-3/4 Ответ: - 3/4
ЗАДАЧА
При каких а оба корня уравнения х2-ах+2=0 лежат на интервале (0;3)?
D≥0,
X0 Є(M,N),
f(M)>0,
f(N)>0.
а2-8 ≥ 0,
а/2 Є (0;3),
9-3а+2 > 0
здесь D=a2-8, х0=а/2 и f(3)=9-3a+2 (смотри сюда – СЛУЧАЙ здесь D=a2-8, х0=а/2 и f(3)=9-3a+2 (смотри сюда – СЛУЧАЙ IV).
Решим получившуюся систему
<=>
|а|≥√8,
а Є (0;6),
а < 11/3
<=>
а ≥ 2√2,
а Є (0;6),
а < 11/3.
Ответ: 2√2 ≤ a ≤ 11/3
a*f(0)<0,
a*f(3)<0.
a*1<0,
a*(9a+4)<0
<=>
<=>
<=>
a*1<0,
a*(9a+4)<0
a<0,
9a2+4a<0
<=>
a<0,
+
-
+
X
-4/9
0
<=>
f(0)=1
f(3)=9a+4
a<0, -4/9 <=> (смотри сюда – Ответ: -4/9
-4/9
СЛУЧАЙ СЛУЧАЙ V)
Задача
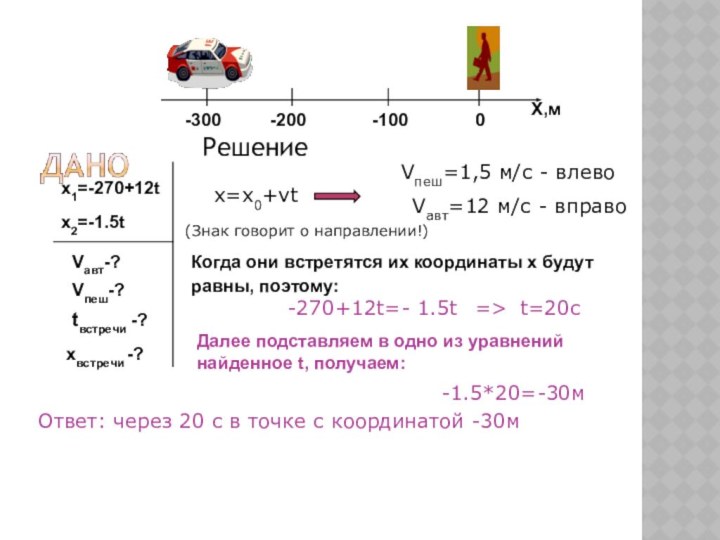
-270+12t=- 1.5t
=>
t=20c
Далее подставляем в одно из уравнений найденное t, получаем:
-1.5*20=-30м
Ответ: через 20 с в точке с координатой -30м
X,м
-200
-100
0
-300
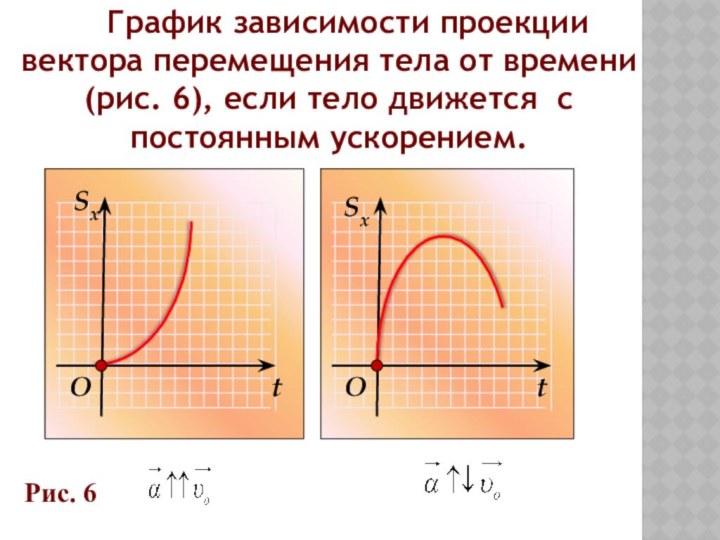
Рис. 6
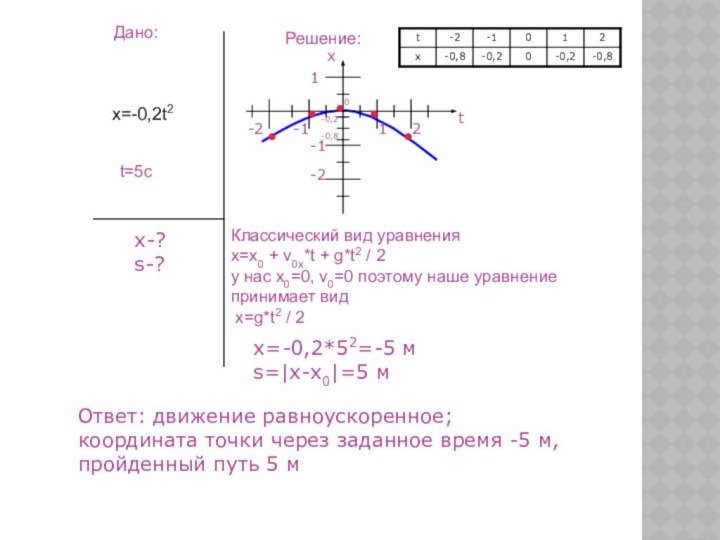
б) х1=2*5+0.2*52=15 м
х2=80-4*5=60 м
х2 - х1=60-15=45 м
в) х2=0 => 0=80-4*t => t=20
х1=2*20+0,2*202=120 м