Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему по физике на тему Решение систем уравнений методом Крамера

Содержание

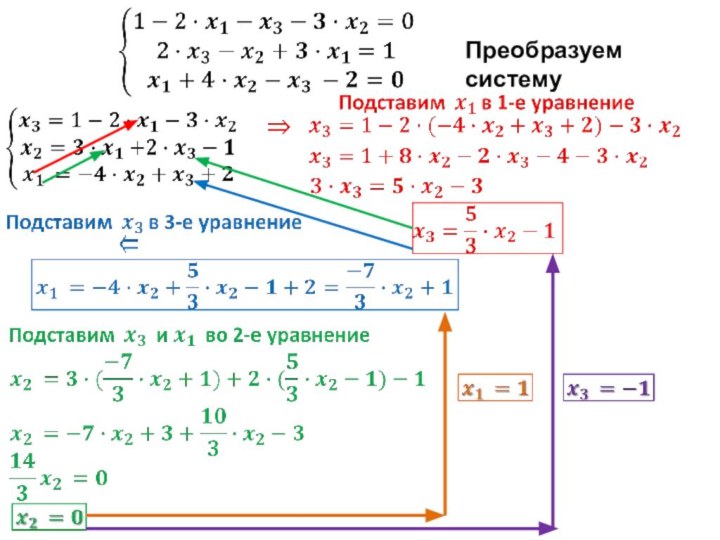
2. Преобразуем систему
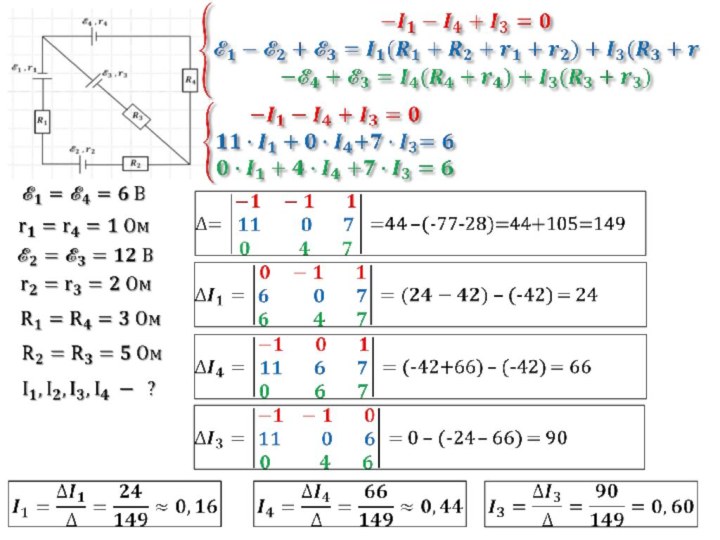
4. Для нахождения её решения вычисляем определителиПо формулам Крамера находим:
5. Метод КрамераМетод Крамера основан на использовании определителей
6. Для решения системы методом Крамера необходимо преобразовать
7. Определение. Определитель, составленный из коэффициентов при неизвестных,
8. Формулы Крамера для нахождения неизвестных:
12. Эту формулу можно легко запомнить с помощью
13. Решение. Находим определитель системы:Следовательно, система является определённой и имеет решение.
14. Для нахождения её решения вычисляем определителиПо формулам Крамера находим:
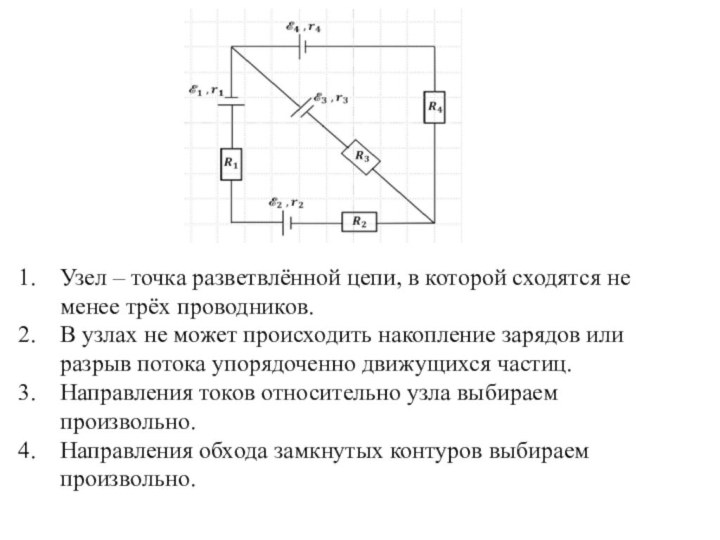
16. Узел – точка разветвлённой цепи, в которой
17. Правила Кирхгофа1) Первое правило Кирхгофа относится к
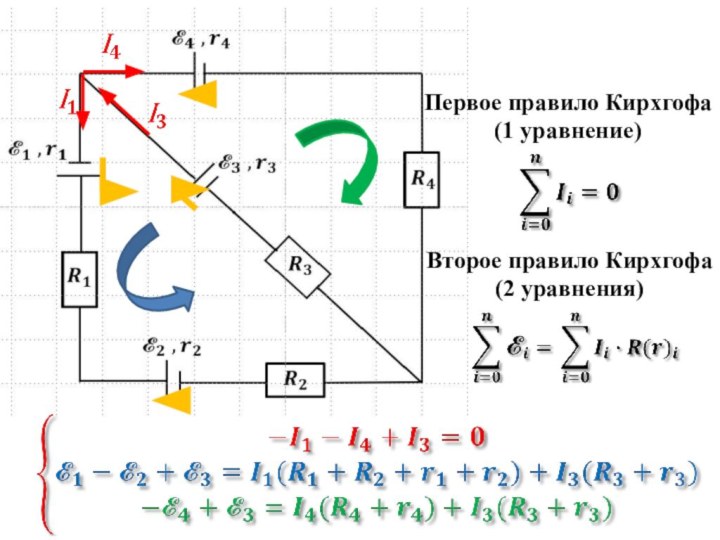
18. Первое правило Кирхгофа (1 уравнение)Второе правило Кирхгофа (2 уравнения)
19. Скачать презентацию
20. Похожие презентации

Преобразуем систему

Главная
Физика
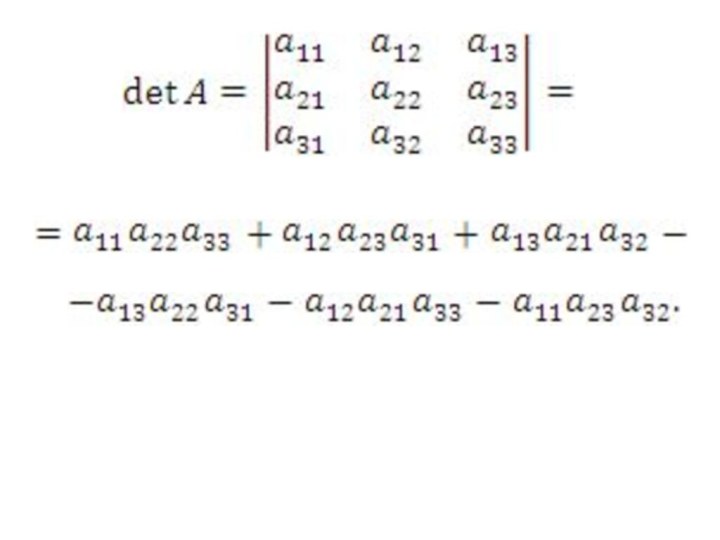
Презентация по физике на тему Решение систем уравнений методом Крамера

Пример 1. Решить систему линейных уравнений:. Выразить из 2-го уравнения х1Подставить выражение для

Презентация по физике на тему Решение систем уравнений методом Крамера

Для нахождения её решения вычисляем определителиПо формулам Крамера находим:

Метод КрамераМетод Крамера основан на использовании определителей в решении систем линейных уравнений.

Для решения системы методом Крамера необходимо преобразовать уравнения:Сгруппировать все члены с неизвестными

Определение. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы (главный определитель)

Формулы Крамера для нахождения неизвестных:

Эту формулу можно легко запомнить с помощью правила треугольников, которое иллюстрируется представленными

Решение. Находим определитель системы:Следовательно, система является определённой и имеет решение.

Узел – точка разветвлённой цепи, в которой сходятся не менее трёх проводников.В

Правила Кирхгофа1) Первое правило Кирхгофа относится к узлам.Алгебраическая сумма сил токов для

Первое правило Кирхгофа (1 уравнение)Второе правило Кирхгофа (2 уравнения)

Слайды презентации

Слайд 2 Преобразуем систему

Слайд 3

Слайд 4 Для нахождения её решения вычисляем определители
По формулам Крамера

находим:

Слайд 5 Метод Крамера
Метод Крамера основан на использовании определителей в

Метод КрамераМетод Крамера основан на использовании определителей в решении систем линейных

решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод

Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Слайд 6 Для решения системы методом Крамера необходимо преобразовать уравнения:
Сгруппировать

Для решения системы методом Крамера необходимо преобразовать уравнения:Сгруппировать все члены с

все члены с неизвестными с одной стороны относительно знака

=, свободные члены с другой.
Расположить неизвестные во всех уравнениях в одинаковом порядке.

Слайд 7 Определение. Определитель, составленный из коэффициентов при неизвестных, называется

Определение. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы (главный

определителем системы (главный определитель) и обозначается ∆
1) Произведение коэффициентов

на главной диагонали берутся со знаком (+).

Решение:

2) Произведение коэффициентов на побочной диагонали берутся со знаком (-).

Слайд 8 Формулы Крамера для нахождения неизвестных:

Слайд 9

Слайд 10

Слайд 11

Слайд 12 Эту формулу можно легко запомнить с помощью правила

Эту формулу можно легко запомнить с помощью правила треугольников, которое иллюстрируется

треугольников, которое иллюстрируется представленными ниже рисунками.
Рис. 1. Произведения элементов,

расположенных на главной диагонали матрицы или в вершинах треугольников, основания которых параллельны этой диагонали, берутся со своими знаками.

Рис. 2. Произведения элементов, расположенных на побочной диагонали матрицы или в вершинах треугольников, основания которых параллельны этой диагонали, берутся с противоположными знаками.

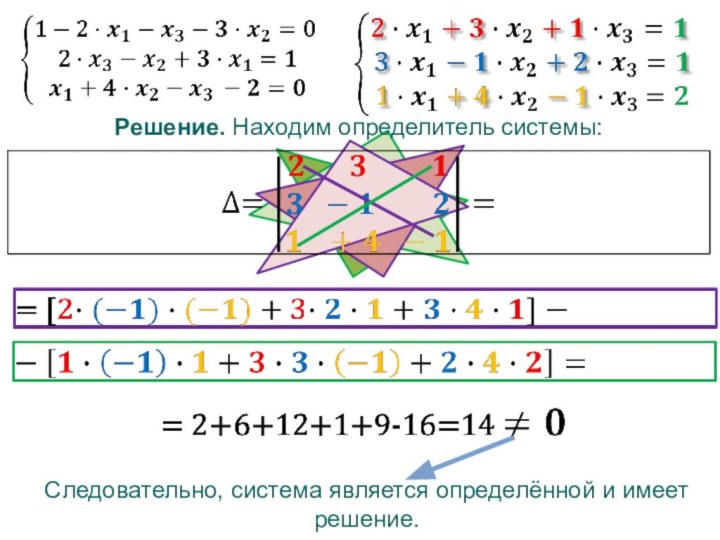
Слайд 13 Решение. Находим определитель системы:
Следовательно, система является определённой и

имеет решение.

Слайд 14 Для нахождения её решения вычисляем определители
По формулам Крамера

находим:

Слайд 15

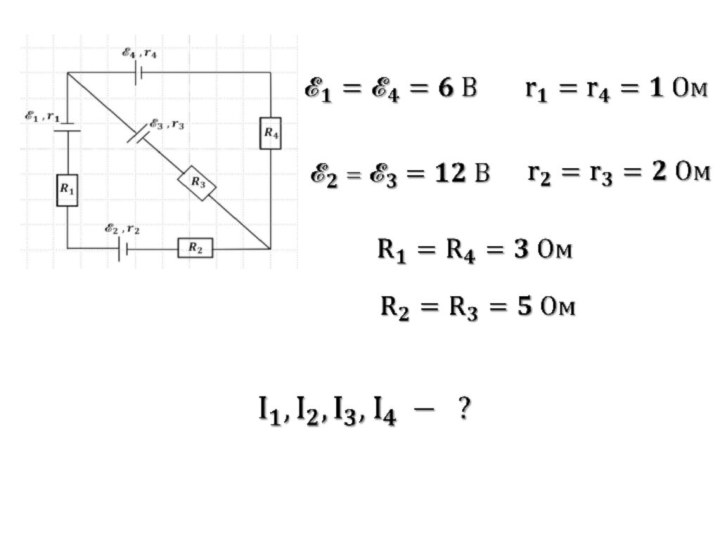
Слайд 16 Узел – точка разветвлённой цепи, в которой сходятся

Узел – точка разветвлённой цепи, в которой сходятся не менее трёх

не менее трёх проводников.
В узлах не может происходить накопление

зарядов или разрыв потока упорядоченно движущихся частиц.
Направления токов относительно узла выбираем произвольно.
Направления обхода замкнутых контуров выбираем произвольно.

Слайд 17 Правила Кирхгофа
1) Первое правило Кирхгофа относится к узлам.
Алгебраическая

Правила Кирхгофа1) Первое правило Кирхгофа относится к узлам.Алгебраическая сумма сил токов

сумма сил токов
для каждого узла равна нулю.
Если ток

втекает в узел, то силу тока
считают положительной, если вытекает из узла, то отрицательной.

2) Второе правило Кирхгофа относится к отдельным замкнутым контурам цепи.
Алгебраическая сумма ЭДС в замкнутом
контуре равна алгебраической сумме
произведений сил токов и сопротивлений
каждого из участков этого контура.
Если на данном участке источник тока создаёт ток, совпадающий по направлению с выбранным направлением обхода контура, то ЭДС считается положительной, в противном случае – отрицательной.
Если произвольно выбранное направление тока совпадает с направлением обхода контура, то силу тока считают положительной, в противном случае – отрицательной.