- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по физике Гидростатический парадокс (7 класс)
Содержание
- 2. На рисунке изображены три сосуда различной формы
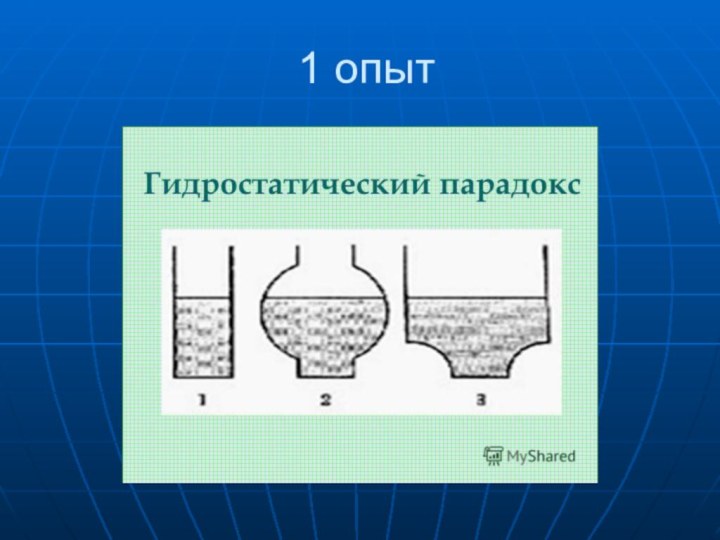
- 3. 1 опыт
- 4. На первый взгляд кажется, что и давление
- 5. 2 опыт
- 6. Мы видим, что резиновые плёнки, являющиеся теперь
- 7. Мы столкнулись с парадоксом (от греч. «парадоксос»
- 8. Давление на дно каждого сосуда можно рассчитать
- 9. Как видим, в последней формуле F =ρghSнет ни
- 10. Блез Паскаль (1623-1662)
- 11. Блез Паскаль приходит к открытию закона, получившего
- 12. Скачать презентацию
- 13. Похожие презентации
На рисунке изображены три сосуда различной формы с одинаковыми площадями их доньев, но с различными диаметрами верхних частей. Очевидно, что если в сосуды до одного и того же уровня налить какой-либо жидкости, то в левом сосуде











Слайд 4
На первый взгляд кажется, что и давление на
дно левого сосуда будет наименьшим, а на дно правого
– наибольшим. Но это – предположение, и его нужно проверить опытом. Заменим прочные донья сосудов на резиновые плёнки и посмотрим, насколько сильно они растягиваются. Взгляните на второй рисунок:
Слайд 6
Мы видим, что резиновые плёнки, являющиеся теперь доньями
сосудов, прогибаются. При этом их движения передаются стрелкам. Опыт
показывает, что при одинаковых высотах столбов воды в сосудах стрелки отклоняются на равное число делений шкалы. Из опыта следует вывод: сила давления жидкости на дно сосуда не зависит от его формы!
Слайд 7
Мы столкнулись с парадоксом (от греч. «парадоксос» –
неожиданный, странный). Более точно он называется гидростатическим парадоксом(от греч. «гидор» –
вода, жидкость и «статос» – неподвижный). Его физический смысл в том, что вес налитой в сосуд жидкости отличается от силы давления на дно (для левого и правого сосудов).Как же выйти из сложившегося затруднительного положения? То есть как «примирить» наше предположение про массу (вес) и результат опыта?
Слайд 8
Давление на дно каждого сосуда можно рассчитать по
формуле p=ρgh.Если в сосуды налита одна и та же
жидкость, то давления будут одинаковы, так как одинаковы высоты столбов жидкости.Силу, с которой жидкость давит на дно каждого сосуда, можно рассчитать по формуле F = pS. Подставляя первую формулу во вторую, мы получим: F =ρghS.. Все величины, стоящие в правой части этого равенства, одинаковы для всех трёх сосудов. Следовательно, будут равны и силы, действующие на донья всех трёх сосудов.