понять излагаемый материал;
усвоить основную часть его на занятии;
составить конспект;
уметь
по ОК составить логический ответ по основным вопросам.знать
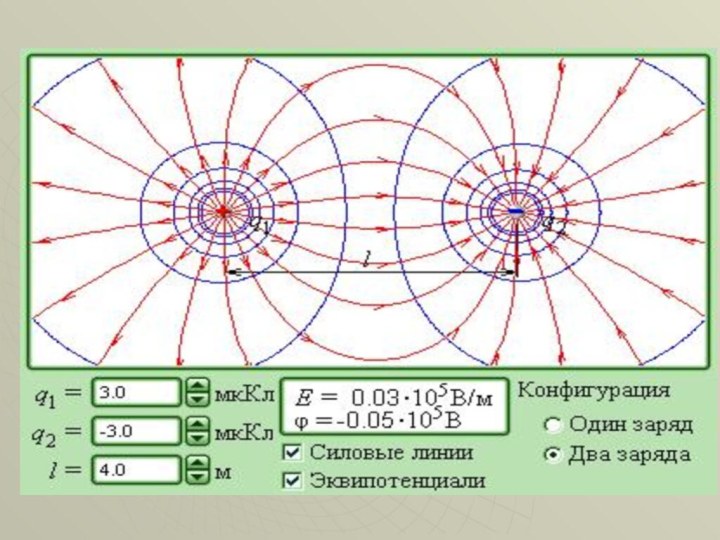
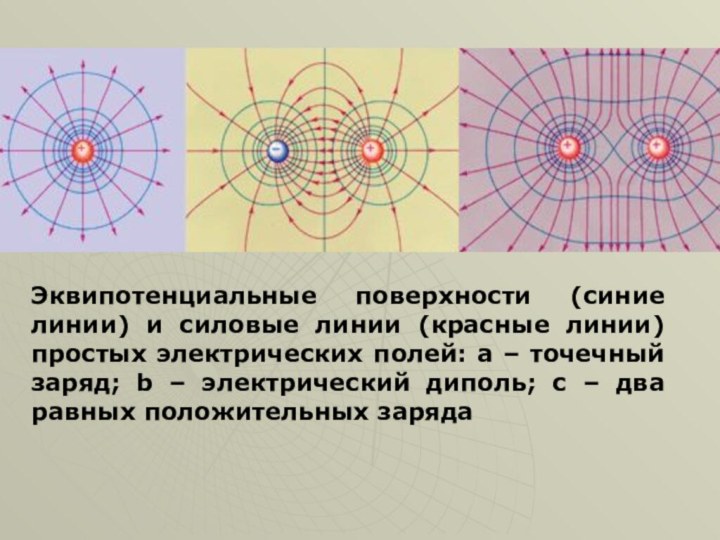
физическую сущность взаимосвязи между напряжённостью и разностью потенциалов;
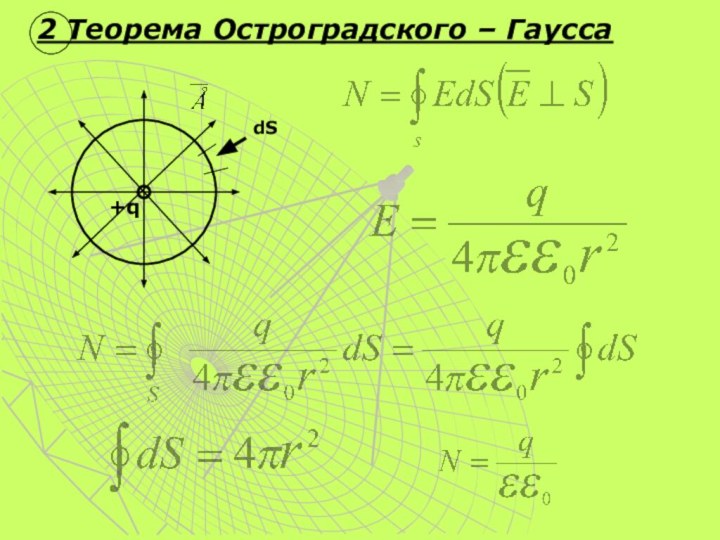
теорему Гаусса для электростатического поля
уметь
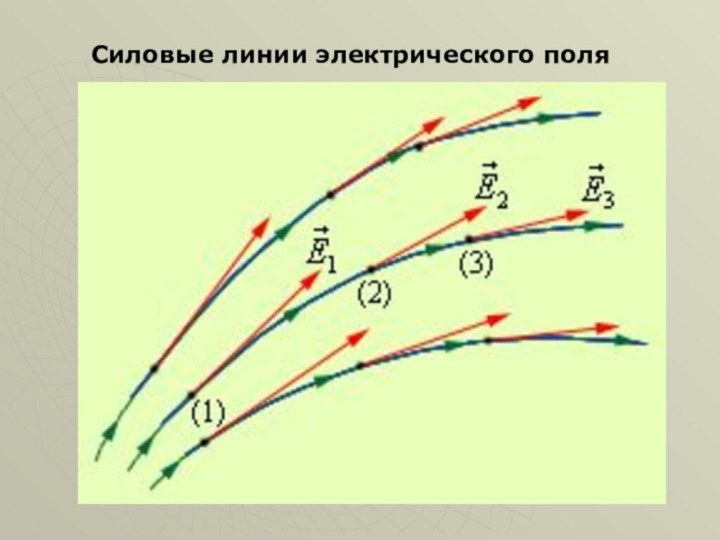
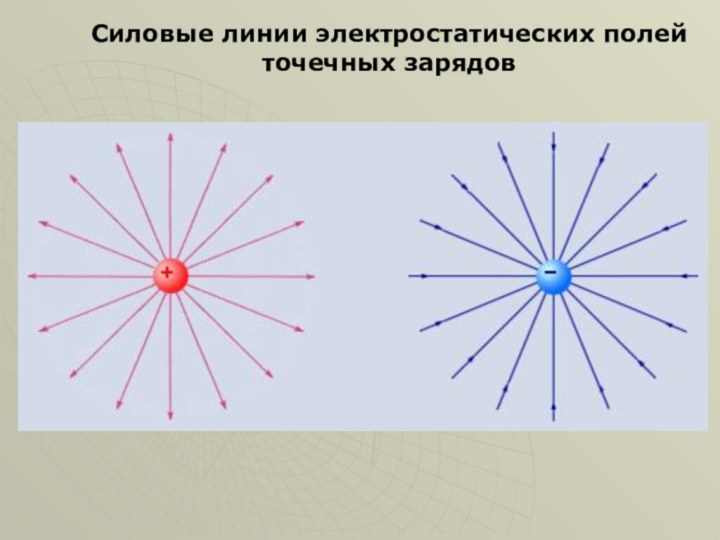
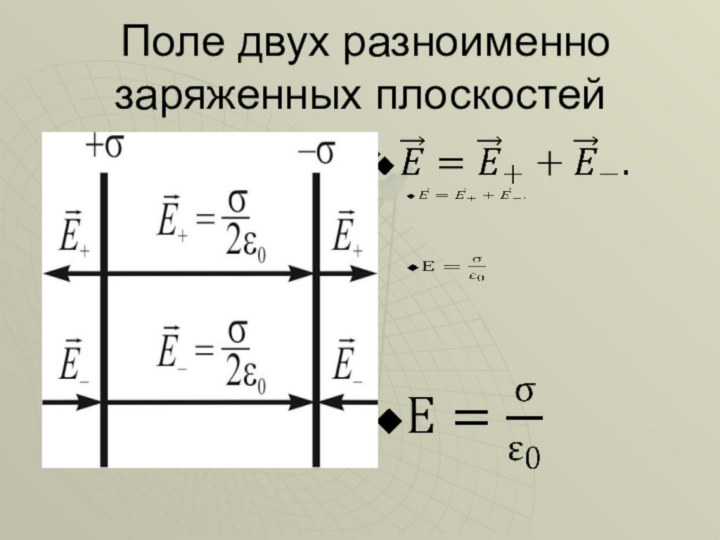
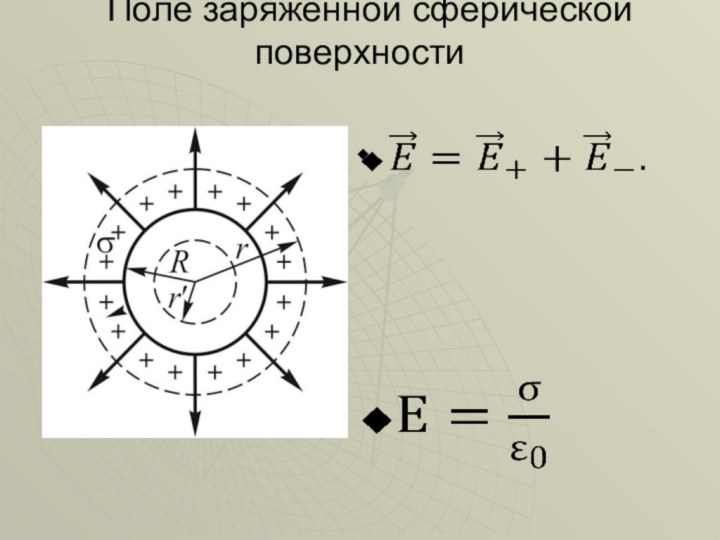
графически изобразить электростатическое поле;
применить теорему Гаусса для расчёта полей