- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Центр масс (центр инерции) системы материальных точек
Содержание
- 2. Цели:Познакомить учащихся с понятием центра масс.Рассмотреть свойства
- 3. Центром масс (центром инерции) системы материальных точек
- 4. Можно записать используя понятие радиуса-вектора:
- 6. Центр масс плоской фигурыДля нахождения центра масс
- 7. Некоторые важные свойства : – если однородное
- 8. Алгоритм решения может быть следующим:Разбиваем сложную фигуру
- 14. Скачать презентацию
- 15. Похожие презентации
Цели:Познакомить учащихся с понятием центра масс.Рассмотреть свойства центра масс для различных тел.Показать алгоритмы нахождения центра масс.Рассмотреть разные способы нахождения цетра масс.











Слайд 2
Цели:
Познакомить учащихся с понятием центра масс.
Рассмотреть свойства центра
масс для различных тел.
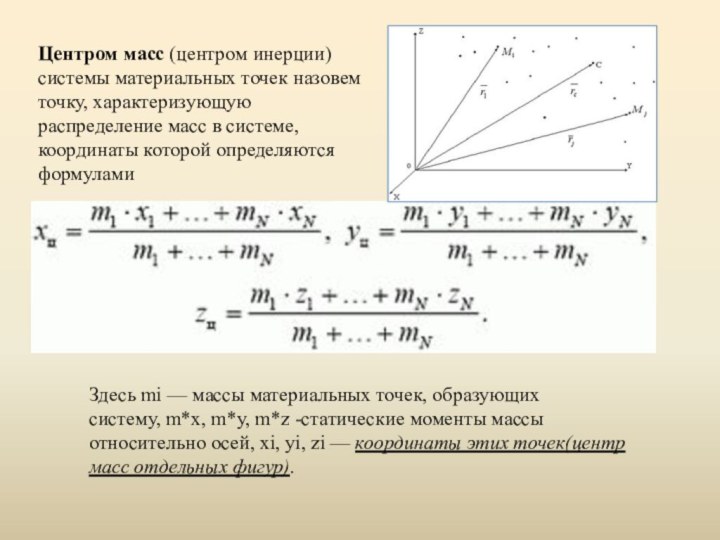
способы нахождения цетра масс.Слайд 3 Центром масс (центром инерции) системы материальных точек назовем
точку, характеризующую распределение масс в системе, координаты которой определяются
формуламиЗдесь mi — массы материальных точек, образующих систему, m*x, m*y, m*z -статические моменты массы относительно осей, xi, yi, zi — координаты этих точек(центр масс отдельных фигур).
Слайд 6
Центр масс плоской фигуры
Для нахождения центра масс плоской
фигуры, имеющей сложносоставную форму,
достаточно эффективен метод ее разбиения
на простые элементы с легко определяемымикоординатами. Сложная конфигурация представляется в виде объединения простых фигур, из которых вырезаны некоторые фрагменты.
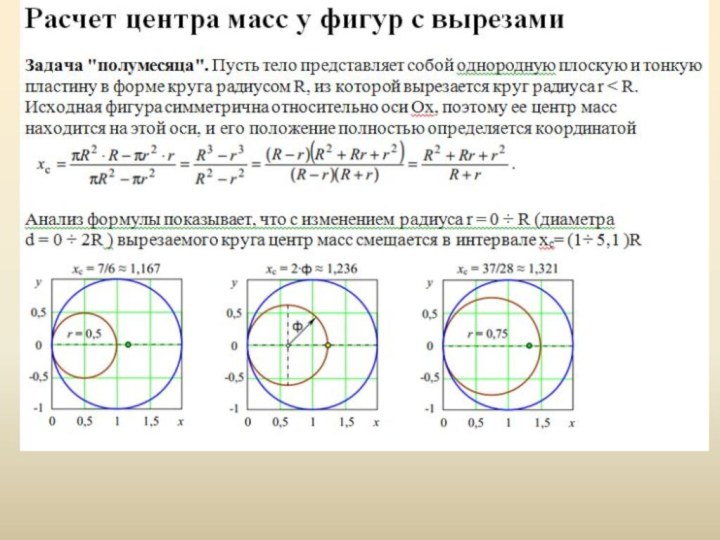
Таким образом, если однородную материальную пластину можно разбить на конечное
число частей с известными положениями центров тяжести, то координаты (положение) ЦМ всей пластины можно вычислить по формулам (метод отрицательных масс)
Т.е у тех элементов в фигуре которых вырезаны части, их массы берутся с минусом .
Уравнение центра масс для плоской фигуры толщиной L, с известными геометрическими данными можно представить
Уравнение центра масс для плоской фигуры толщиной L, с известными геометрическими данными можно представить
Тк.m=ρV, V=SL , то m пропорциональна S
Формулы равнозначны.
Слайд 7
Некоторые важные свойства :
– если однородное тело
имеет центр (ось, плоскость) симметрии, то ЦМ совпадает с
этим
центром (лежит на этой оси, в плоскости); – если ЦМ отдельных частей тела лежат на одной прямой (плоскости), то и ЦМ лежит
на этой прямой (плоскости);
– если тело имеет полости (пустоты), то его можно рассматривать как систему,
состоящую из сплошного тела и тел в форме пустот, имеющих отрицательную массу (метод
отрицательных масс);
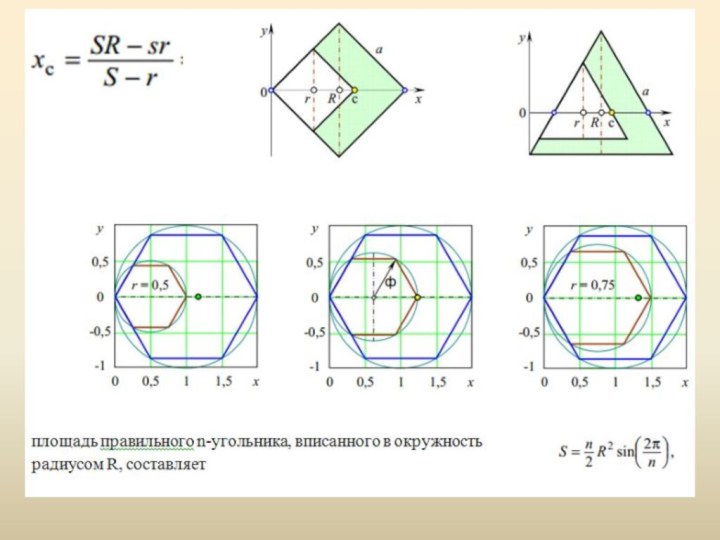
– ЦМ фигур и тел правильной геометрической формы совпадает с геометрическим
центром;
– ЦМ правильного многоугольника совпадает с центром поворотной симметрии
Слайд 8
Алгоритм решения может быть следующим:
Разбиваем сложную фигуру на
элементарные, центр масс(центр симметрии) которых легко находится
Записываем уравнения для
центра масс, где х1, х2 … расстояния до центров масс этих элементарных фигур.В уравнениях перед значениями ставиться минус, если взятая нами элементарная фигура является полостью или вырезом.





























