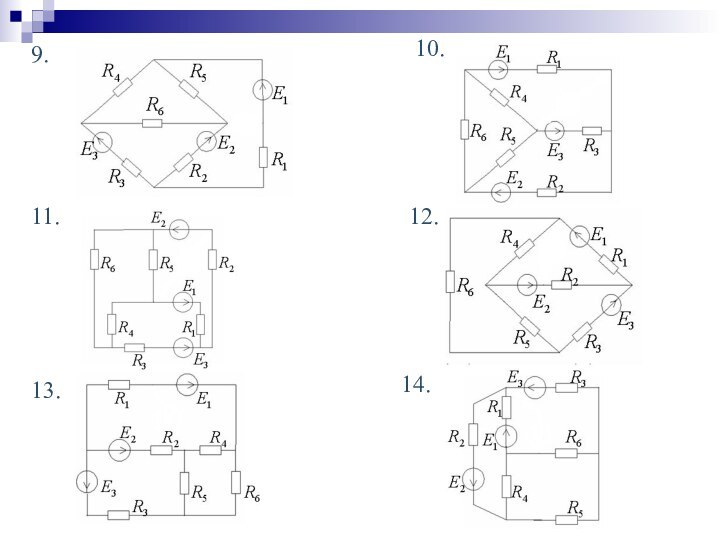
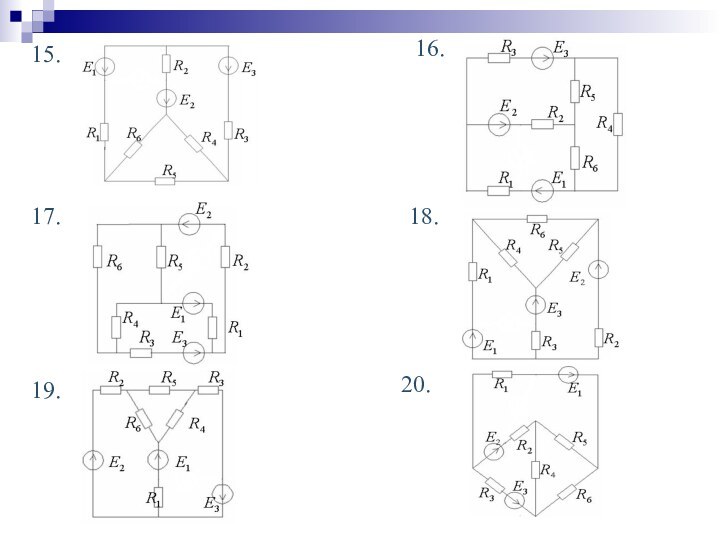
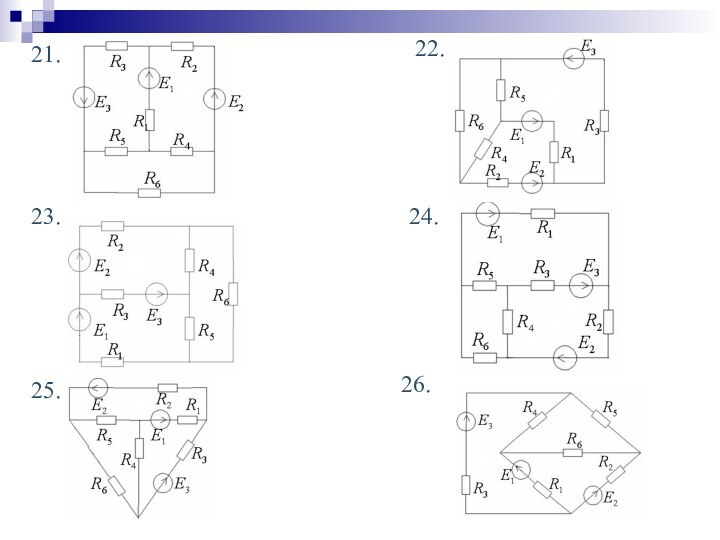
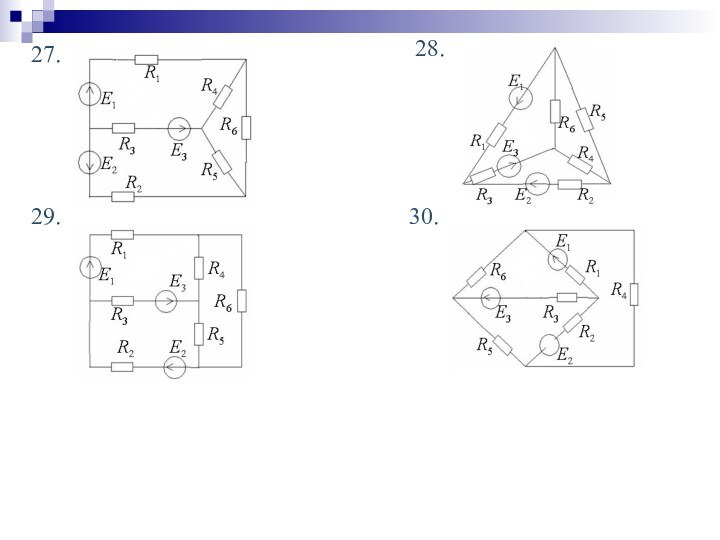
Кирхгофа, метод контурных токов, баланс мощностей.
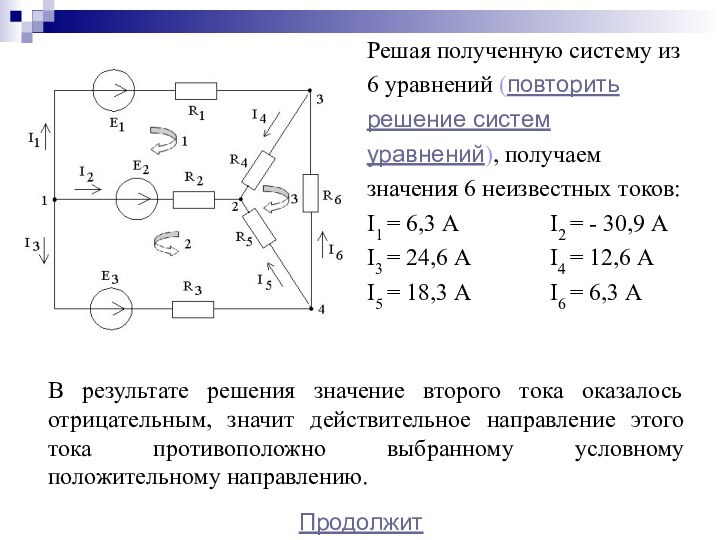
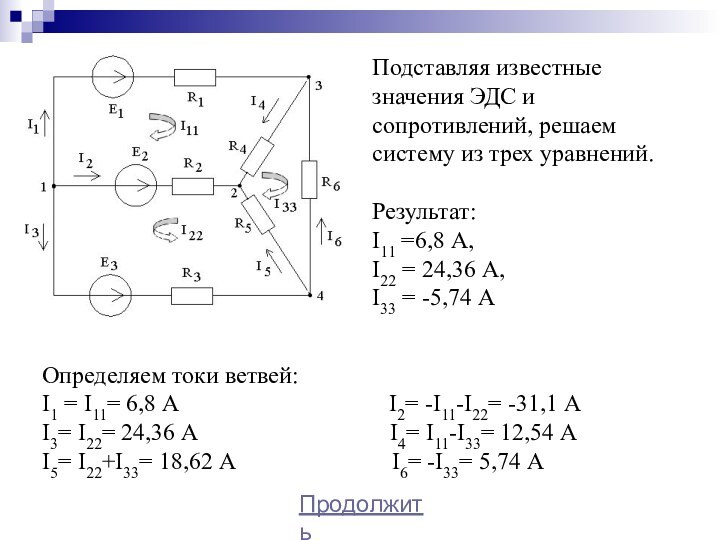
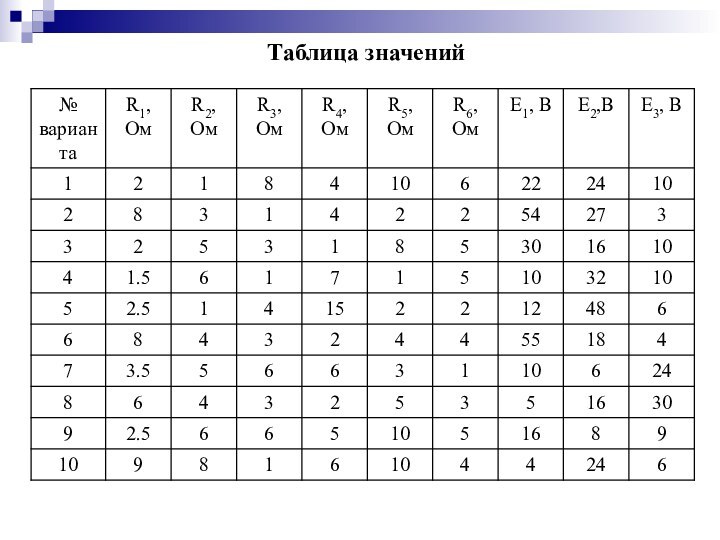
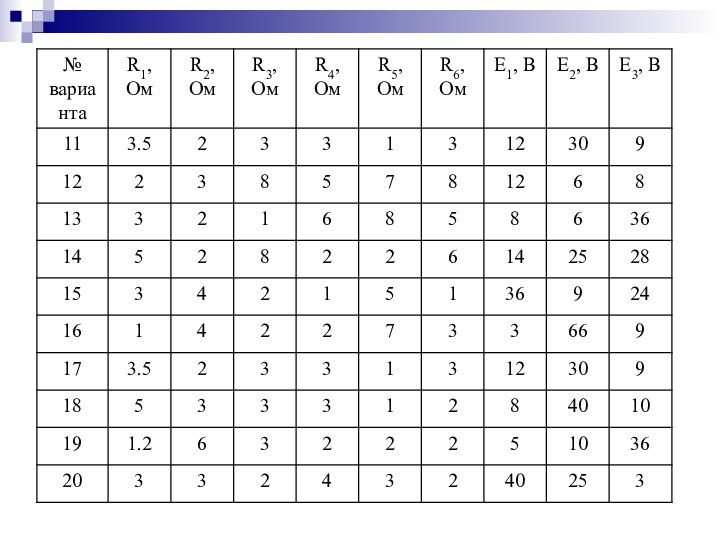
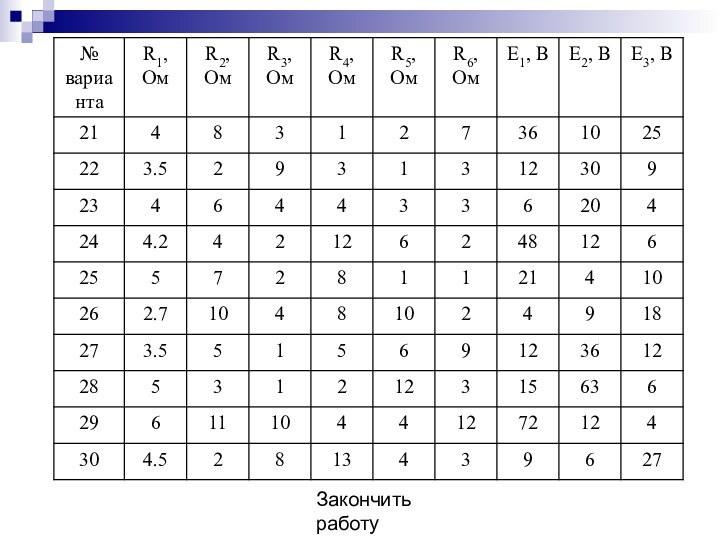
2. Практическое задание: расчет
сложной линейной цепи постоянного тока.3. Математическая поддержка: решение систем уравнений.
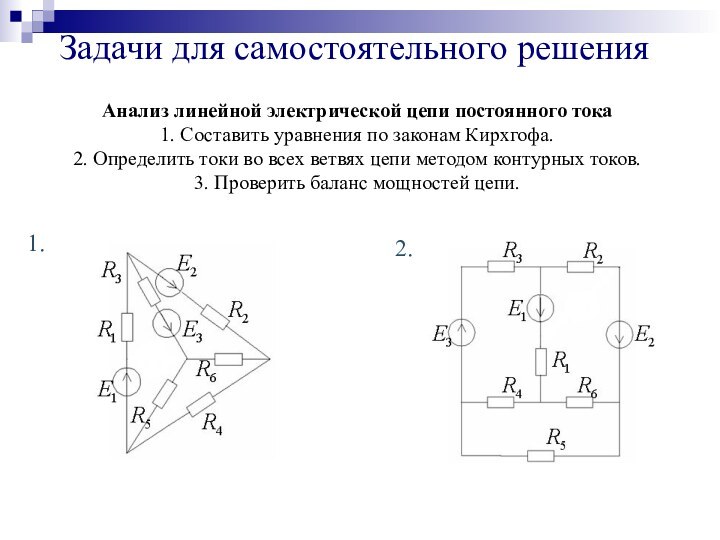
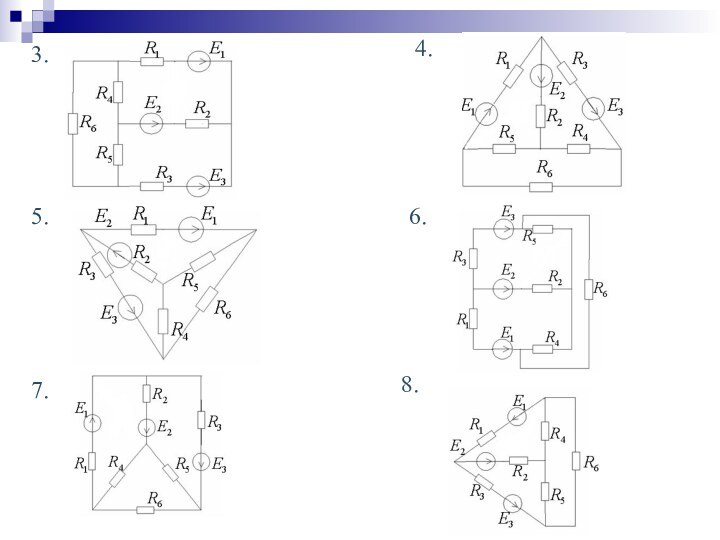
4. Задачи для самостоятельного решения.
Продолжить