Слайд 2
Виды измерений
Измерения в геодезии являются количественной и качественной
основой для изучения Земли, для получения исходной информации при
решении всех инженерно-геологических задач и выполнения топографических работ.
Любое измерение выражается количественной характеристикой (величиной угла, длиной линии, превышением, площадью участка местности и т.п.) и имеет качественную сторону, которая характеризует точность полученного результата.
Слайд 3
Измеренные и вычисленные величины
Величины, которые получают в процессе
производства геодезических работ, можно классифицировать на измеренные и вычисленные.
Измеренные
- получают непосредственно, путём сравнения величины с единицей средства измерения.
Вычисленные – получают косвенно, или как функцию двух или нескольких, непосредственно измеренных величин. (Например, площадь прямоугольника как произведение длин его сторон, полученных непосредственными измерениями)
Слайд 4
Результаты измерений
Под результатом измерения предусматривается конечный результат, который
получается в процессе всех произведённых измерений и вычислений. (К
примеру, высота точки, её координаты, площадь участка и т.п.)
Результаты измерений в своей группе могут быть равноточными и неравноточными.
Слайд 5
Равноточные и неравноточные измерения
Если измерения выполнены прибором одного
и того же класса точности, по одной и той
же методике (программе), в одинаковых внешних условиях, одним и тем же наблюдателем (либо наблюдателями одной квалификации), то такие измерения относят к равноточным. При несоблюдении хотя бы одного из перечисленных выше условий результаты измерений классифицируют как неравноточные.
Слайд 6
Необходимые и избыточные измерения
Число измеренных величин и число
измерений может быть необходимым и избыточным.
Числом необходимых измеренных величин
является минимально необходимое их число, при котором обеспечивается решение поставленной задачи. Число же измеренных величин, превышающих число необходимых, называется числом избыточных величин. В геодезии принято обязательным получать и избыточные величины, что обеспечивает обнаружение грубых погрешностей и промахов, позволяет повысить точность результатов измерений.
Слайд 7
Надёжность результатов измерений
Все избыточные измерения повышают надёжность результатов,
а также их точность, но в то же время
и увеличивают объем работ, и часто прирост увеличения точности становится экономически нецелесообразным из-за большого числа наблюдений.
Слайд 8
Классификация погрешностей измерений
Любые измерения, как бы они тщательно
не выполнялись, сопровождаются погрешностями, которые представляют собой отклонение результата
измерения от истинной его величины.
Отклонения результатов измерения от истинной величины возникают из-за изменения условий измерений. Изменение условий измерений вызывает также изменение характеристик средства измерения, приводит к появлению личных ошибок (погрешностей) самого наблюдателя, колебаниям видимого положения наблюдаемого объекта (точки).
Слайд 11
Грубые и систематические погрешности
В результате измерений могут появиться
грубые погрешности, проявляющиеся в виде промахов и просчётов наблюдателя,
из-за незамеченных неисправностей прибора, либо из-за резких изменений внешних условий наблюдений. Результаты грубых измерений обнаруживаются при повторных измерениях, отбраковываются и заменяются новыми.
Внешние условия измерений, изменение характеристик измерительного средства могут вызвать появление погрешностей одностороннего (одного знака) или знакопеременного вида – систематических погрешностей.
Слайд 12
Случайные погрешности
Источниками случайных погрешностей в измерениях являются неподдающиеся
учёту мгновенные изменения (флуктуации)
внешних условий, которые приводят к неопределённости в каждый момент времени в видимом положении наблюдаемой цели, к относительно мгновенным изменениям характеристик прибора, погрешностям считывания по шкалам прибора и устройств, устанавливаемых на цели и др. По своей величине каждая из составляющих случайных погрешностей является малой, однако в некоторых случаях их совместное действие может быть существенным. В первом приближении случайную погрешность можно определить как разность результата измерения и истинного значения, если в измеренной величине отсутствует грубая погрешность и учтена погрешность систематическая.
Слайд 13
Свойства случайных погрешностей
Слайд 14
Свойство 1
При выполнении измерений одной величины равновероятно
появление случайных погрешностей, равных по величине, но противоположных по
знаку.
Слайд 15
Свойство 2
Малые по абсолютной величине погрешности встречаются
чаще, чем большие
Слайд 19
Средняя квадратическая погрешность
Средняя квадратическая погрешность (СКП) является мерой
точности результатов измерений, либо функций
измеренных величин, и является вероятностной характеристикой.
Слайд 20
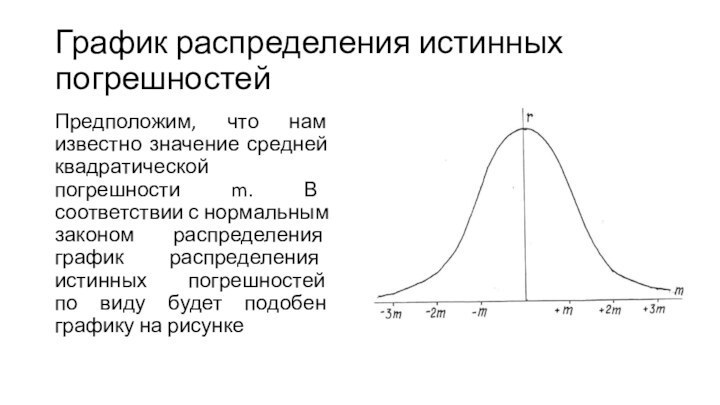
График распределения истинных погрешностей
Предположим, что нам известно значение
средней квадратической погрешности m. В соответствии с нормальным законом
распределения график распределения истинных погрешностей по виду будет подобен графику на рисунке
Слайд 21
Параметр r характеризует частоту (или частость) появления случайных
погрешностей той или иной величины и знака. При этом
вероятность появления погрешностей в заданном наперед диапазоне, например, ±∆, определяется площадью фигуры, ограниченной кривой распределения и отрезками ординат при значениях +∆ и −∆.
Для нормального закона распределения вероятность появления погрешностей в установленных диапазонах равна следующим значениям :
для диапазона ±∆ → Р = 68,3% (≈ 68%);
для диапазона ±2∆→ Р = 95,5% (≈ 95%);
для диапазона ±3∆→ Р = 99,7% (практически 100%).
Слайд 22
Таким образом, только в 3-х случаях из
1000 может появиться погрешность,
превышающая значение 3∆. Такие погрешности принято считать грубыми, и результаты измерений, содержащие такие погрешности, исключают из дальнейшей обработки. В некоторых случаях, для ужесточения требований к точности измерений, устанавливают предельную погрешность до 2∆ (или до 2m).
Слайд 23
Коэффициент Стьюдента
Часто значение СКП указывают с коэффициентом t
(коэффициент Стьюдента), который и определяет доверительный вероятностный интервал (х
± tm) результата измерений при установленном уровне вероятности Р
Слайд 24
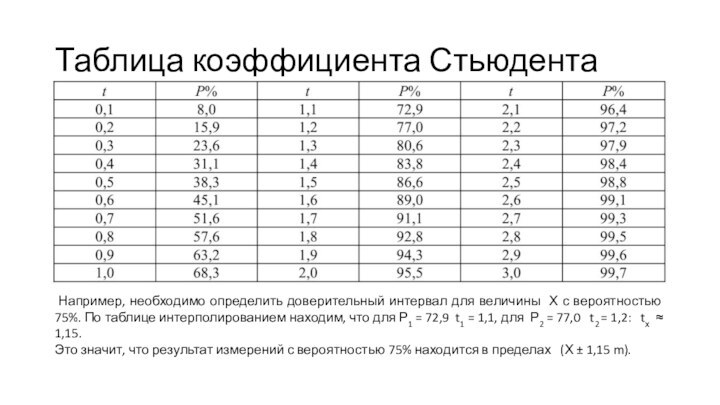
Таблица коэффициента Стьюдента
Например, необходимо определить доверительный интервал
для величины Х с вероятностью 75%. По таблице интерполированием
находим, что для Р1 = 72,9 t1 = 1,1, для Р2 = 77,0 t2 = 1,2: tх ≈ 1,15.
Это значит, что результат измерений с вероятностью 75% находится в пределах (Х ± 1,15 m).
Слайд 25
Формула Гаусса для СКП
Если измеряемая величина Х известна,
то значение СКП определяется по формуле Гаусса:
Слайд 26
Формула Бесселя
Для случаев, когда измеряемая
величина неизвестна, используется формула Бесселя:
При
возрастании числа измерений значения СКП, полученные по формулам Гаусса и Бесселя, становятся практически одинаковыми
Слайд 27
Погрешность погрешности измерений
Поскольку число измерений
является ограниченным, то сама СКП
содержит погрешность, определяемую по приближенной формуле:
Слайд 28
Средние квадратические погрешности функции измеренных величин
Слайд 29
Правила определения СКП функций следующие
1. Выполнить последовательно дифференцирование
функции отдельно по каждому из аргументов,
считая остальные аргументы постоянными числами (коэффициентами).
2. Полученные выражения умножить на СКП аргументов, по которым производилось дифференцирование функции и возвести полученные выражения каждое отдельно в квадрат.
3. Записать полученные выражения в виде суммы под знаком квадратного корня.
Слайд 30
Средняя квадратическая погрешность двойных равноточных однородных измерений
В абсолютном
большинстве случаев в геодезических работах производят двукратные измерения однородных
величин: длин линий (примерно одинаковых по величине), горизонтальных углов (образованных примерно одинаковыми по величине сторонами), превышений и др. Также, как и при многократных измерениях одной величины, здесь возникает необходимость оценки точности измерений, т.е. определения средней квадратической погрешности разности двойных измерений.
Слайд 31
Предположим, что мы имеем ряд из n парных
равноточных измерений хi и x’i , для которых можно
составить разности di :
В этом случае, полагая, что в исследуемом ряду в разностях не содержатся систематические погрешности, можно записать для средней квадратической погрешности разности:
Слайд 32
Поскольку измерения равноточные, то можно записать, что
с учётом
вышеприведённого, можно записать, что
Слайд 33
Двойные измерения одной величины позволяют в большой степени
обнаружить систематические погрешности одного знака и примерно одной величины
(односторонние погрешности). Если систематические погрешности отсутствуют, то сумма разностей двойных измерений весьма близка к нулю, т.е. [d] = 0. Наличие в измерениях систематической погрешности приводит к ее накоплению в сумме разностей двойных измерений, в связи с чем получится величина Q = [d]. При n измерениях доля накопленной систематической погрешности в каждой разности будет составлять
Слайд 34
Если из значений разностей двойных
измерений исключить величину систематической погрешности,
то СКП
разности можно вычислить по формуле
а СКП одного измерения – по формуле
Слайд 35
Вес измерения
Если в качестве веса результата измерения взять
число, которое характеризует точность, то по смыслу слова вес
можно сказать, что, чем больше вес результата, тем выше его точность (тем меньше погрешность, с которой получен данный результат). Т.е. вес находится в обратно пропорциональной зависимости от погрешности результата. Пусть точность измерения какой-либо величины характеризуется средней квадратической погрешностью m, тогда вес Р определяют как отношение
Слайд 36
Значение с может быть любым, кроме нуля, но
для анализируемой группы результатов измерений его принимают равным примерно
среднему значению m по группе, поэтому значения весов результатов измерений не будут слишком большими или слишком маленькими.
Величина СКП зависит от числа измерений, а это значит, что от числа измерений зависит и вес: чем с большим числом измерений получен тот или иной результат, тем больше его вес.
Слайд 37
Среднее взвешенное значение
x1о , x2о и x3о -
средние арифметические значения для серий измерений