ускорение;
период.
Рассмотреть всевозможные случаи применения движения по окружности:
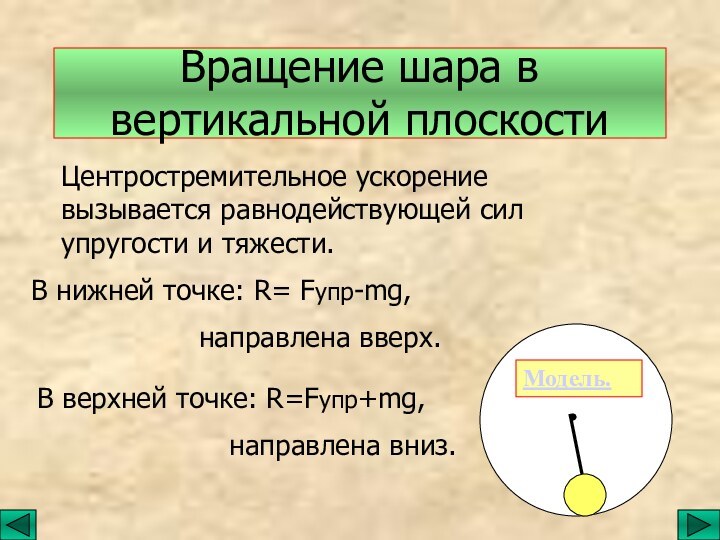
вращение тела;
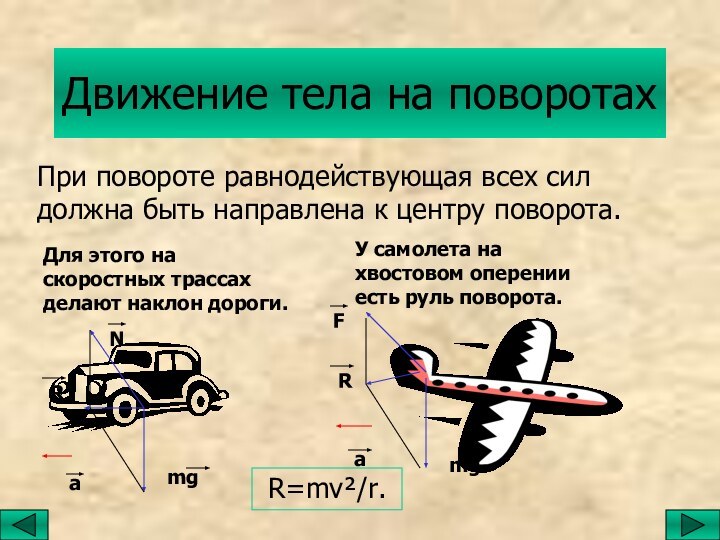
движение
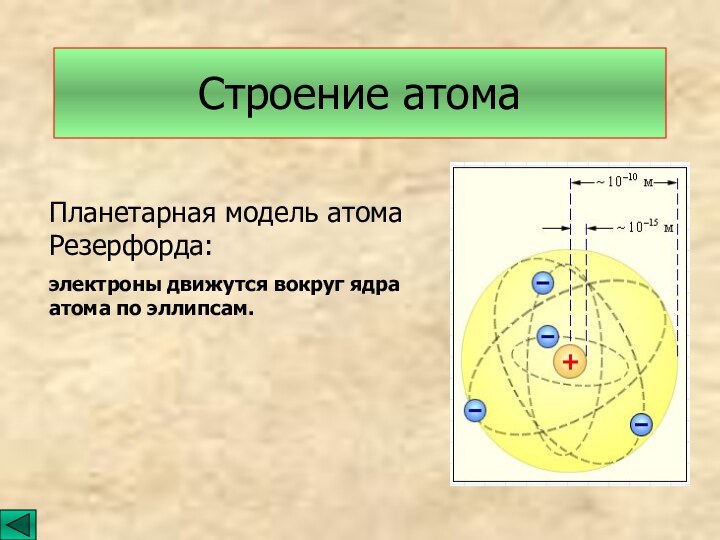
на поворотах;движение планет;
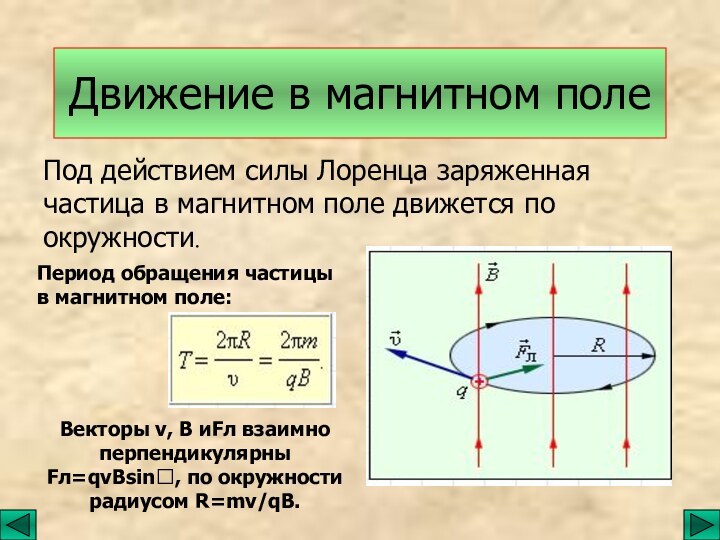
движение заряженных частиц.
Цели