Слайд 2
Тема 9. ВЗАИМОДЕЙСТВИЕ СВЕТА С ВЕЩЕСТВОМ
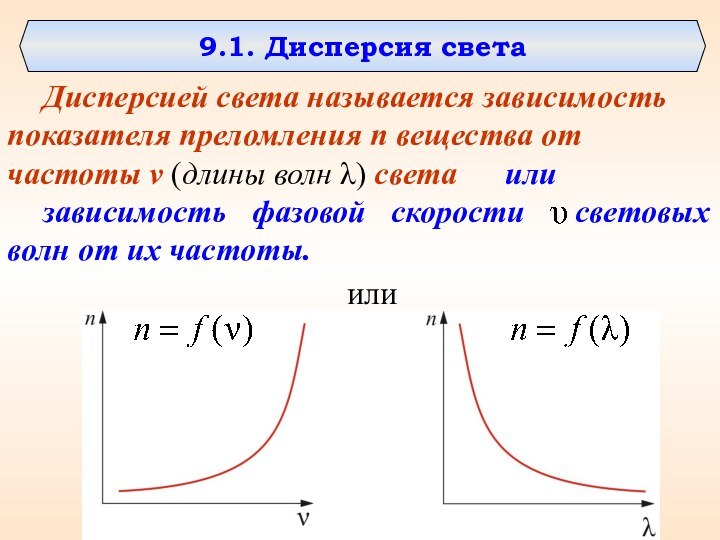
9.1. Дисперсия света
Сегодня:
9.2. Нормальная и аномальная дисперсии
9.3. Классическая теория дисперсии
9.4. Поглощение
(абсорбция света)
9.5. Излучение Вавилова-Черенкова
Слайд 3
Дисперсией света называется зависимость показателя преломления n вещества
от частоты ν (длины волн λ) света
или
зависимость фазовой скорости световых волн от их частоты.
9.1. Дисперсия света
или
Слайд 4
Разложение светового пучка в дисперсионный спектр вследствие дисперсии
света на стеклянной призме
Слайд 5
Угол отклонения лучей призмой тем
больше, чем больше преломляющий угол призмы
Лучи разных длин
волн после прохождения призмы отклоняются на разные углы. Пучок белого света за призмой разлагается в спектр, который называется дисперсионным или призматическим
Слайд 6
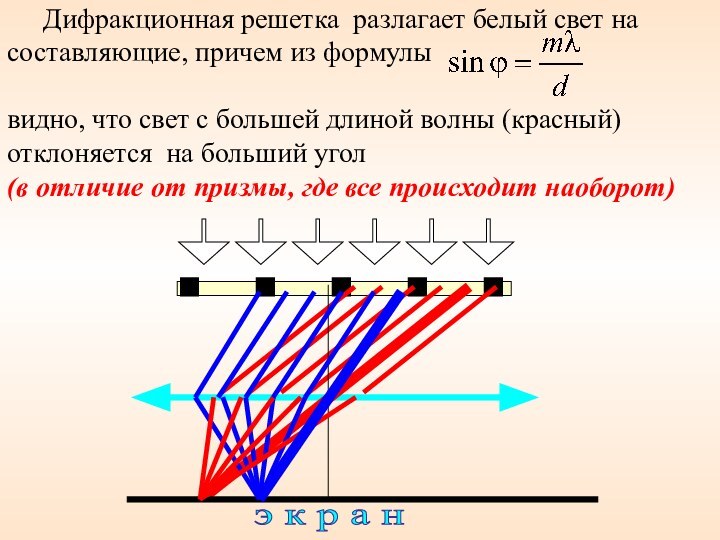
Дифракционная решетка разлагает белый свет на составляющие,
причем из формулы
видно, что свет с большей длиной волны (красный) отклоняется на больший угол
(в отличие от призмы, где все происходит наоборот)
э к р а н
Слайд 7
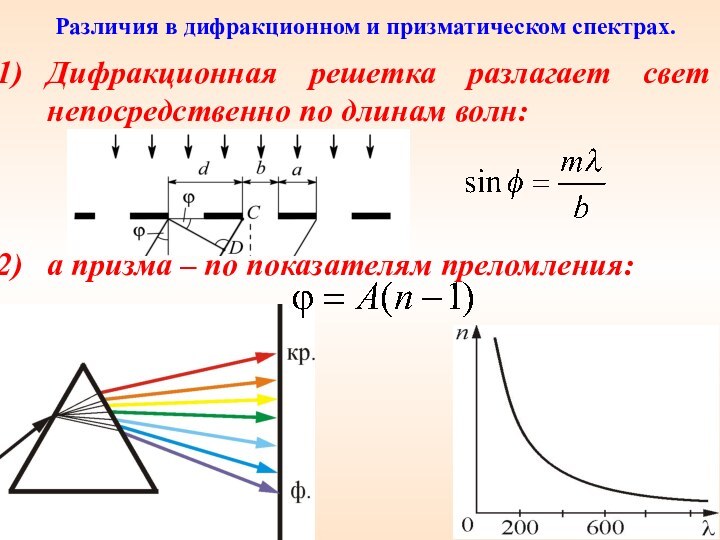
Различия в дифракционном и
призматическом спектрах.
Дифракционная решетка разлагает свет непосредственно по длинам
волн:
а призма – по показателям преломления:
Слайд 8
2) Составные цвета в дифракционном и призматическом спектрах
располагаются различно: красные лучи, имеющие большую длину волны, чем
фиолетовые, отклоняются диф - решеткой сильнее, а в призме наоборот.
Слайд 9
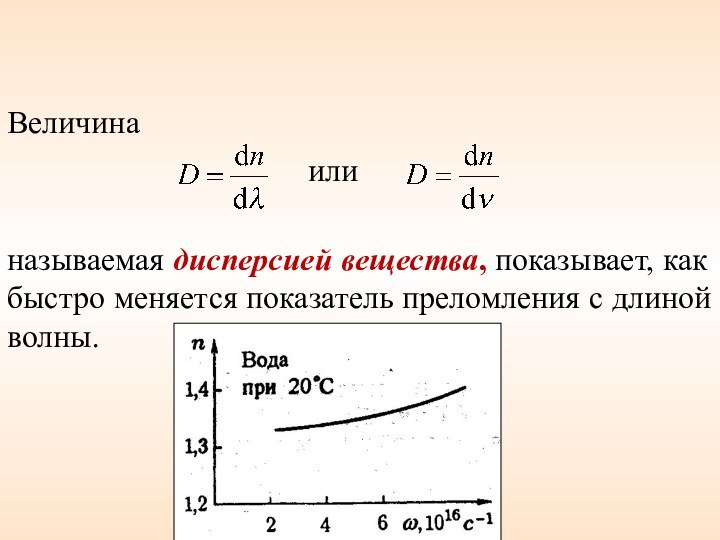
Величина
или
называемая дисперсией вещества, показывает, как быстро меняется
показатель преломления с длиной волны.
Слайд 10
9.2. Нормальная и аномальная дисперсии
Области значения ν, в
которых
или
(9.2.1)
соответствует нормальной дисперсии света
(с ростом частоты ν, показатель преломления n увеличивается).
Дисперсия называется аномальной, если
или
(9.2.2)
т.е. с ростом частоты ν показатель преломления n уменьшается.
Слайд 11
Зависимости n от ν и λ
Рисунок 9.4.
Рисунок 9.5
В недиспергирующей среде
u – групповая
скорость, υ – фазовая скорость
Слайд 12
(9.2.3)
Т.о., при нормальной дисперсии u < υ, а
значит
u < c и
При аномальной дисперсии, т.к.
то u > υ
и, в частности,
если
, то u > c
Слайд 13
9.3. Классическая теория дисперсии
линейная оптика
Если
, то
нелинейная
оптика
Слайд 14
Дисперсия света является результатом взаимодействия
электромагнитной волны с заряженными частицами, входящими в состав вещества.
Теория Максвелла не могла объяснить это явление, так как тогда не было известно о сложном строении атома.
Классическая теория дисперсии была разработана Х.А. Лоренцем лишь после создания им электронной теории строения вещества.
Он показал, что
и ε – тоже зависит от частоты.
Слайд 15
Для видимого света
существует поляризация электрически упругого смещения. Смещаются в основном валентные электроны.
В процессе вынужденных (под действием падающей световой волны) колебаний электронов с частотой ν (частота вынуждающей силы), периодически изменяются дипольные электрические моменты атомов, частота которых тоже равна ν.
Среднее расстояние между атомами вещества много меньше протяженности одного цуга волн. Следовательно, вторичные волны, излучаемые большим числом соседних атомов, когерентны как между собой, так и с первичной волной.
При сложении этих волн они интерферируют, в результате этой интерференции и получаются все наблюдаемые оптические явления, связанные со взаимодействием света с веществом.
Слайд 16
Оптический электрон совершает вынужденные колебания
под действием следующих сил:
• возвращающей квазиупругой силы
•
силы сопротивления
• его решение:
(9.3.3)
Диф. уравнение колебаний электрона:
Слайд 17
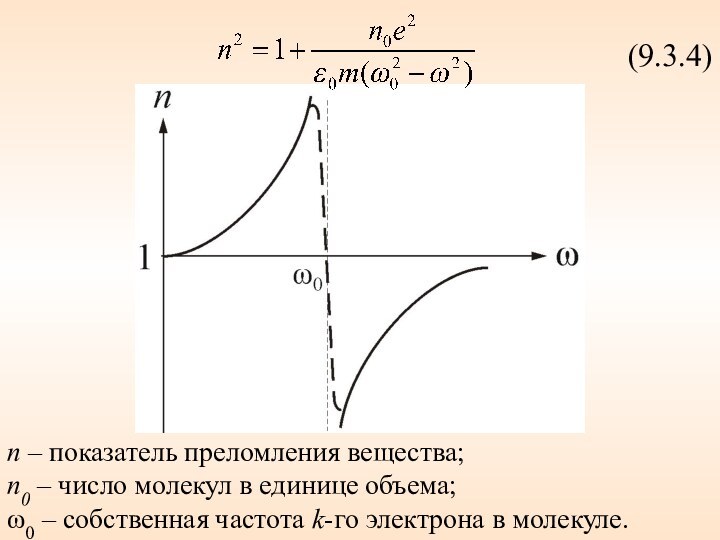
(9.3.4)
n – показатель преломления вещества;
n0 – число молекул
в единице объема;
ω0 – собственная частота k-го электрона в
молекуле.
Слайд 18
9.4. Поглощение (абсорбция света)
Поглощением (абсорбцией) света называется явление
потери энергии световой волной, проходящей через вещество.
.
Для плоской
волны, распространяющейся вдоль оси x, имеем:
П. Бугер (1698 – 1758) – французский ученый
– интенсивность волны на входе в среду,
α – коэффициент поглощения
Закон Бугера:
Слайд 19
При
,
Следовательно, коэффициент
поглощения – физическая величина, численно равная обратному значению толщины
слоя вещества, в котором интенсивность волны убывает в е = 2,72 раз.
Зависимость коэффициента поглощения от длины волны определяет спектр поглощения материала.
Слайд 20
В веществе (например в газе) может присутствовать
несколько сортов частиц, участвующих в колебаниях под действием распространяющейся
электромагнитной волны.
Если эти частицы слабо взаимодействуют, то коэффициент поглощения мал для широкого спектра частот, и лишь в узких областях он резко возрастает
У веществ, атомы (молекулы) которых слабо взаимодействуют друг с другом (газы, пары металлов): α ≠ 0 в узком интервале длин волн (шириной ~10-2 Å) – резкие максимумы, соответствующие резонансным частотам колебаний электронов внутри атомов.
Слайд 21
При увеличении давления газа полосы
поглощения уширяются (рис. а).
В жидком
состоянии они сливаются, и спектр поглощения принимает вид, показанный на рис.б.
Причиной уширения является усиление связи атомов (молекул) в среде.
б
а
Слайд 22
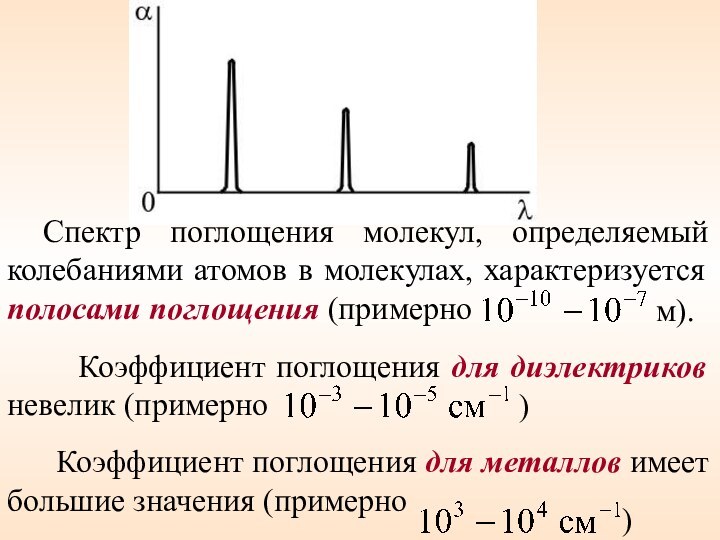
Спектр поглощения молекул, определяемый колебаниями атомов в молекулах,
характеризуется полосами поглощения (примерно
м).
Коэффициент
поглощения для диэлектриков невелик (примерно
)
Коэффициент поглощения для металлов имеет большие значения (примерно
)
Слайд 23
Металлы практически непрозрачны для света из-за наличия
свободных электронов:
При падении света
свободные
электроны приходят в движение,
возникают быстропеременные токи,
выделяется тепло Джоуля – Ленца,
- энергия световой волны переходит во внутреннюю энергию металла.
Слайд 24
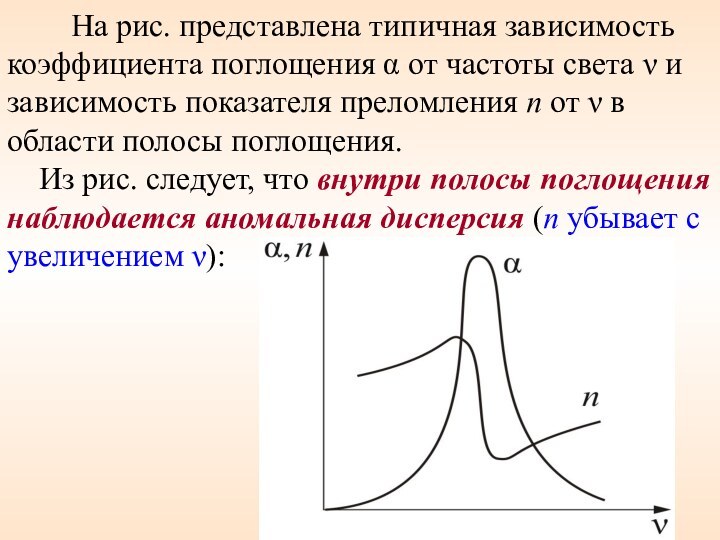
На рис. представлена типичная
зависимость коэффициента поглощения α от частоты света ν и
зависимость показателя преломления n от ν в области полосы поглощения.
Из рис. следует, что внутри полосы поглощения наблюдается аномальная дисперсия (n убывает с увеличением ν): 6 6
Слайд 25
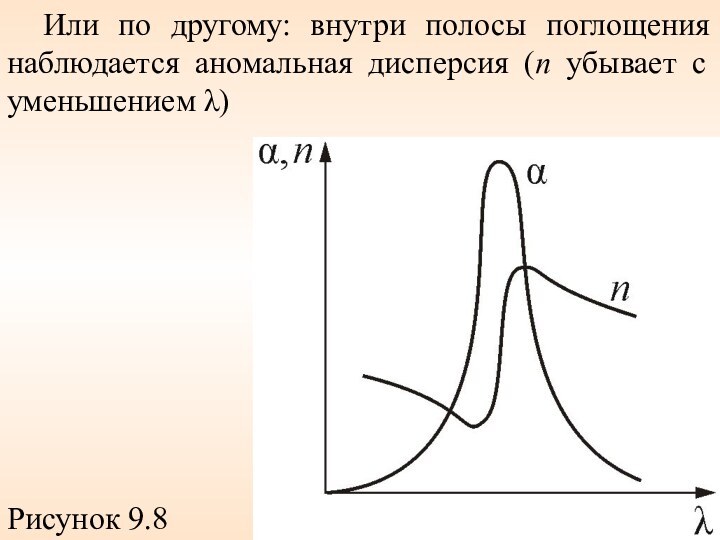
Или по другому: внутри полосы поглощения наблюдается аномальная
дисперсия (n убывает с уменьшением λ)
Рисунок 9.8
Слайд 27
Зависимостью коэффициента поглощения от частоты (длины волны) объясняется
окрашенность поглощающих тел.
Разнообразие пределов
селективного (избирательного) поглощения у различных веществ объясняет разнообразие и богатство цветов и красок, наблюдающееся в окружающем мире.
Слайд 28
«… Видел радугу на небе,
На востоке, и тихонько
Говорил:
« Что там, Нокомис?»
И Нокомис отвечала:
« Это Мускодэ
на небе;
Все цветы лесов зеленых,
Все болотные кувшинки,
На земле, когда увянут,
Расцветают снова в небе.»
По мотивам легенды
североамериканских индейцев.
Слайд 29
Чем меньшей энергией обладает свет, тем быстрее он
поглощается:
Длинноволновые части спектра, красный и
оранжевый цвета, поглощаются почти полностью уже на глубине 5-8 метров.
Затем исчезают желтые цвета.
Гораздо дольше проникают синий и зеленый.
Слайд 30
Рассеяние света
В неоднородной среде световые волны дифрагируют
на неоднородностях среды – рассеиваются.
Среды с ярко выраженной оптической
неоднородностью называют мутными:
Дымы – взвеси в газах мельчайших твердых частиц;
Туманы - взвеси в газах мельчайших капель жидкости;
Взвеси (суспензии) – жидкости с плавающими в них твердыми частицами;
Эмульсии – взвеси частиц одной жидкости в другой, не растворяющие первую;
Некоторые твердые тела (опал, перламутр…)
Слайд 31
Если размеры неоднородностей малы по сравнению с длиной
волны:
В результате рассеяния света интенсивность в направлении распространения убывает
быстрее, чем в случае только поглощения:
α’ – коэффициент экстинкции.
Интенсивность рассеянного света:
Рассеянный свет является частично поляризованным.
- закон Рэлея.
Слайд 32
Если размеры неоднородностей сравнимы с длиной волны:
Электроны, находящиеся
в различных местах неоднородности, колеблются с заметным сдвигом по
фазе.
В результате интенсивность рассеянного света:
Молекулярное рассеяние – рассеяние, обусловленное флуктуациями плотности жидкости или газа.
Флуктуации вызваны хаотическим движением молекул вещества.
Слайд 34
Голубые и синие лучи рассеиваются
сильнее, чем желтые и красные (закон Рэлея), обуславливая голубой
цвет неба
Рассеянный свет (раннее утро)
Слайд 35
Рассеяние света, как правило, значительно интенсивнее поглощения,
Т.о.
с увеличением глубины преобладает уже не направленный, а рассеянный
свет, идущий со всех сторон.
Поэтому на достаточно больших глубинах, вне видимости дна и поверхности, можно стать жертвой эффекта так называемой «голубой пелены» и потерять представление о том, где верх, а где низ.
Рассеяние света под водой
Слайд 36
Спектральный анализ
Явление поглощения широко используется в абсорбционном спектральном анализе
смеси газов, основанном на измерениях спектров частот и интенсивностей линий (полос) поглощения.
Структура спектров поглощения определяется составом и строением молекул, поэтому изучение спектров поглощения является одним из основных методов количественного и качественного исследования веществ.
Слайд 37
Спектральные аппараты
Ход лучей в спектрографе
1.
Через узкую щель проходит пучок света.
2. Линза №1 делает
пучок света
параллельным.
3. Призма раскладывает белый свет по длинам волн на спектр.
4. Линза №2 собирает разошедший пучок излучения по длинам волн в разные концы экрана.
5. Фотопластинка фиксирует спектр и получается спектограмма.
Призменный спектральный аппарат – спектрограф.
Слайд 38
Спектральный анализ
Метод определения химического состава по его спектру.
Атомы любого химического элемента дают спектр, не похожий на
спектры всех других элементов: они способны излучать строго определенный набор длин волн.
Видимая часть солнечного излучения при изучении с помощью спектроанализирующих приборов оказывается неоднородной – в спектре наблюдаются линии поглощения, впервые описанные в 1814 году И. Фраунгофером.
Спектральный анализ позволяет получить информацию о составе Солнца, поскольку определенный набор спектральных линий исключительно точно характеризует химический элемент. Так, с помощью наблюдений спектра Солнца был открыт гелий.
С помощью спектрального анализа узнали, что звезды состоят из тех же самых элементов, которые имеются и на Земле.
1.
Слайд 39
2.
С помощью спектрального анализа можно обнаружить данный элемент
в составе сложного вещества. Благодаря универсальности спектральный анализ является
основным методом контроля состава вещества в металлургии, машиностроении, атомной индустрии.
Лабораторная электролизная установка
для анализа металлов «ЭЛАМ».
Установка предназначена для проведения
весового электролитического анализа меди,
свинца, кобальта и др. металлов в сплавах
и чистых металлах.
Стационарно – искровые
оптико - эмиссонные спектрометры
«МЕТАЛСКАН –2500».
Предназначены для точного анализа
металлов и сплавов, включая цветные,
сплавы черных металлов и чугуны.
Слайд 41
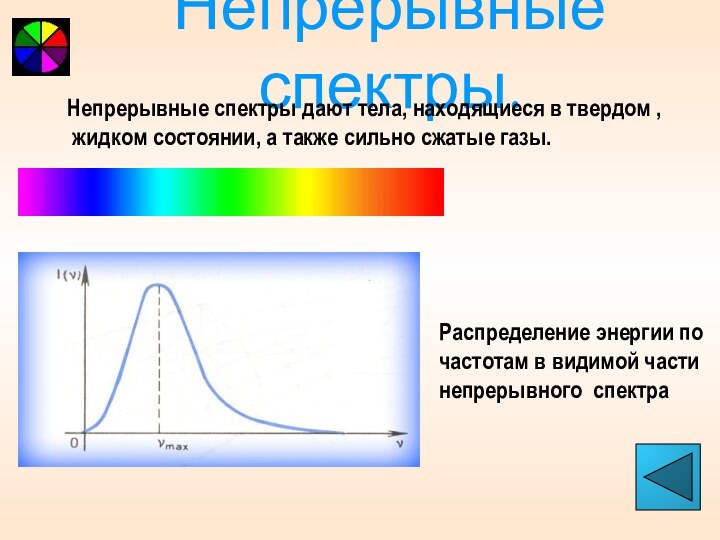
Непрерывные спектры.
Непрерывные спектры дают тела, находящиеся в твердом
,
жидком состоянии, а также сильно сжатые газы.
Распределение
энергии по
частотам в видимой части
непрерывного спектра
Слайд 42
Линейчатые спектры.
Примерное распределение
спектральной плотности
интенсивности излучения
в линейчатом
спектре.
Линейчатые спектры дают все вещества в газообразном
атомарном состоянии.
Изолированные атомы
излучают строго определенные длины волн.
Слайд 43
Полосатый спектр
Элетронный полосатый спектр азота N2
Полосатые спектры в
отличие от линейчатых спектров создаются не
атомами, а молекулами, не
связанными или слабо связанными
друг с другом.
Слайд 44
Спектры испускания
и поглощения
Спектры испускания:
1- сплошной;
2- натрия;
3- водорода;
4-
гелия.
Спектры поглощения:
5- солнечный;
6- натрия;
7- водорода;
8- гелия.
Слайд 45
9.5. Излучение Вавилова-Черенкова
В 1934 году
П.А.Черенков, и С.Н. Вавилов, обнаружили особый вид свечения жидкости
под действием γ-лучей радия.
В 1937 году И.Е. Тамм и И.М. Франк объяснили механизм свечения
В 1940 году В.Л. Гинзбург создал квантовую теорию
Излучение Вавилова-Черенкова это излучение электрически заряженной частицы, движущейся в среде с групповой скоростью u, превышающей фазовую скорость света в этой среде :
Слайд 46
P.A.Cherenkov show picture of UR Pakhra, 1977
Слайд 47
При движении заряженной частицы в изотропной
среде со
скоростью
элементарные волны
будут представлять собой сферы,
находящиеся одна в другой,
распространяющиеся со скоростью
Рисунок 9.9
Слайд 48
Скорость движения меньше фазовой скорости
Слайд 49
Скорость движения источника
равна фазовой скорости
Слайд 50
Скорость движения источника
выше фазовой скорости
Слайд 52
Если частица движется быстрее, чем распространяются волны в
среде, то соответствующие элементарным волнам сферы пересекаются, и их
общая огибающая (волновая поверхность) представляет собой конус с вершиной в точке, совпадающей с мгновенным положением движущейся частицы. Нормали к образующим конуса определяют волновые векторы, т.е. направления распространения света. Угол, который составляет волновой вектор с направлением движения частицы, удовлетворяет соотношению:
.
Слайд 53
Частица движется быстрее, чем распространяются волны в
среде
Слайд 54
Нормали к образующим конуса определяют
волновые векторы распространения света. В этих направлениях вторичные волны
будут усиливаться и формировать излучение Вавилова–Черенкова. Свет, возникающий на каждом малом участке траектории частицы, распространяется вдоль образующей конуса, ось которого совпадает с направлением движения электрона
, а угол при вершине равен 2
Слайд 56
В жидкостях и твердых
телах условие
начинает выполняться для электронов при энергиях
,
а для протонов
Описанный эффект используют в счетчиках Черенкова, предназначенных для регистрации заряженных микрочастиц (электронов, протонов, мезонов, и т.п.). В них световая вспышка, возникающая при движении частицы, преобразуется в электрический сигнал с помощью фотоумножителя, который и регистрируется.
В некоторых черенковских счетчиках можно определить угол и по условию
.
оценить скорость частицы и, зная массу, определить ее энергию.