Слайд 2
МОЛЕКУЛЯРНАЯ
ФИЗИКА
ТЕРМОДИНАМИКА
Т П У
Доцент кафедры
Общей физики
Кузнецов Сергей Иванович
Сегодня
Слайд 3
Тема 6. ЭНТРОПИЯ. ВТОРОЕ И ТРЕТЬЕ НАЧАЛА ТЕРМОДИНАМИКИ
6.1.
Приведенная теплота. Энтропия
6.2. Изменение энтропии
6.3. Поведение энтропии в процессах
изменения агрегатного состояния
6.4. Изменение энтропии в обратимых и необратимых процессах
6.5. Второе начало термодинамики
6.6. Свободная и связанная энергии
6.7. Статистический смысл энтропии
6.8. Третье начало термодинамики
Слайд 4
6.1. Приведенная теплота. Энтропия
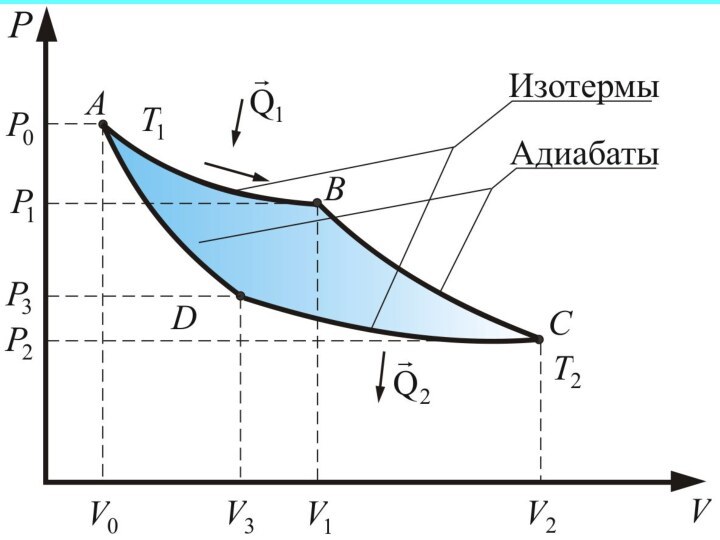
Из рассмотренного цикла
Карно (п. 5.4) видно, что равны между собой отношения
теплот к температурам, при которых они были получены или отданы в изотермическом процессе:
Слайд 5
Отношение теплоты Q в изотермическом
процессе к температуре, при которой происходила передача теплоты, называется
приведенной теплотой :
(6.1.1)
Для подсчета приведенной теплоты в произвольном процессе необходимо разбить этот процесс на бесконечно малые участки, где Т можно считать константой. Приведенная теплота на таком участке будет равна
Слайд 7
Суммируя приведенную теплоту на всех участках процесса, получим:
Тогда
в обратимом цикле Карно имеем:
Слайд 8
Этот результат справедлив для любого обратимого процесса.
Таким
образом, для процесса, происходящего по замкнутому циклу
(6.1.2)
Из равенства нулю интеграла, взятого по замкнутому контуру, следует, что подынтегральное выражение
- есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние.
Слайд 9
Это позволяет ввести новую функцию состояния S:
(6.1.3)
Функция состояния, полный дифференциал
которой равен , называется энтропией.
Энтропия S – это отношение получен-ной или отданной теплоты к температу-ре, при которой происходил этот процесс.
Слайд 10
Понятие энтропии было впервые введено Рудольфом Клаузиусом в
1865 г.
Для обратимых процессов изменение энтропии:
(6.1.4)
- это выражение называется равенство Клаузиуса.
Клаузиус Рудольф Юлиус
Эмануэль (1822 – 1888) –
немецкий физик-теоретик, один
из создателей термодинамики и
кинетической теории газов. Его
работы посвящены молекулярной физике, термодинамике, теории паровых машин, теоретической механике, математической физике. Развивая идеи Н. Карно, точно сформулировал принцип эквивалентности теплоты и работы.
Слайд 12
В 1850 г. получил общие соотношения между теплотой
и механической работой (первое начало термодинамики) и разработал идеальный
термодинамический цикл паровой машины (цикл Ранкина-Клаузиуса). Ввел понятие энтропии.
Слайд 13
6.2. Изменение энтропии в изопроцессах
Энтропия системы является функцией ее состояния, определенная с точностью
до произвольной постоянной.
Если система совершает равновесный переход из состояния 1 в состояние 2, то изменение энтропии:
(6.2.1)
Слайд 14
Таким образом, по этой формуле можно определить энтропию
лишь с точностью до аддитивной постоянной, т.е. начало энтропии произвольно.
Физический смысл имеет лишь разность энтропий.
Исходя из этого, найдем изменения энтропии в процессах идеального газа.
Слайд 16
т.е. изменение энтропии S12 идеального газа при переходе
его из состояния 1 в состояние 2 не зависит
от вида перехода 1 2.
Каждый из изопроцессов идеального газа характеризуется своим изменением энтропии, а именно:
изохорический: ,т.к., V1= V2
т.к. Р1 = Р2,
изотермический:
т.к.
адиабатический:
адиабатический процесс называют изоэнтропийным процессом, т.к.
Слайд 18
Изменение энтропии в изопроцессах:
Слайд 19
6.3. Поведение энтропии в процессах изменения агрегатного состояния
Рассмотрим три агрегатных состояния: твердое, жидкое и газообразное и
два перехода к ним.
Фазовый переход «твердое тело – жидкость»
Из школьного курса физики хорошо известны четыре факта об этом переходе.
Слайд 20
1. Переход вещества из твердого состояния (фазы) в
жидкое называется плавлением, а обратный – кристаллизация.
2. При плавлении
система поглощает тепло, а при отвердевании – отдает….тепло.
3. В процессе плавления температура системы остается постоянной до тех пор, пока вся система не расплавится эта температура называется температурой плавления.
Слайд 21
4. Закон плавления: количество тепла Q, которое необходимо
для плавления вещества массой dm, пропорционально этой массе:
(6.3.1)
Коэффициент пропорциональности λ есть константа, зависящая только от вещества системы и называемая удельной теплотой плавления.
Слайд 22
Этот закон справедлив и для кристаллизации, правда, с
одним отличием: Q в этом случае – тепло выделяемое
системой.
В обобщенном виде закон можно записать так:
при плавлении
при кристаллизации
Слайд 23
Изменение энтропии в процессе этого фазового перехода можно
найти просто, если считать процесс равновесным.
Это вполне допустимое приближение,
если считать, что разность температур между системой и тем объектом, который поставляет системе тепло, не слишком велика, намного меньше температуры плавления.
Слайд 24
Тогда можно использовать термодинамический смысл энтропии: с точки
зрения термодинамики энтропия – это такая функция состояния системы,
изменение которой dS в элементарном равновесном процессе равно отношению порции тепла Q, которое система получает в этом процессе, к температуре системы Т:
.
Подставим сюда выражение для Q, получим:
.
Слайд 26
Так как температура системы в данном фазовом переходе
не меняется и равна температуре плавления, то подынтегральное выражение
это величина, которая в ходе процесса не меняется, поэтому она от массы m вещества не зависит. Тогда:
. (6.3.4)
Слайд 27
Из этой формулы следует, что при плавлении энтропия
возрастает, а при кристаллизации уменьшается.
Физический смысл этого результата
достаточно ясен:
фазовая область молекулы в твердом теле гораздо меньше, чем в жидкости, так как в твердом теле каждой молекуле доступна только малая область пространства между соседними узлами кристаллической решетки, а в жидкости молекулы занимают всю область пространства.
Слайд 28
Поэтому при равной температуре энтропия твердого тела меньше
энтропии жидкости.
Это означает, что твердое тело представляет собой более
упорядоченную, и менее хаотичную систему, поэтому и энтропия его меньше, чем у жидкости.
Слайд 29
Фазовый переход «жидкость – газ»
Этот переход
обладает всеми свойствами перехода «твердое тело – жидкость».
Существует четыре факта также знакомые из школьного курса физики.
1: переход вещества из жидкости в газовую фазу называется испарением, а обратный переход – конденсацией.
Слайд 30
2: при испарении система поглощает тепло, при конденсации
– теряет.
3: процессы испарения и конденсации протекают в широком
диапазоне температур, но фазовым переходом они являются лишь тогда, когда процесс захватывает всю массу вещества. Это происходит при определенной температуре Тк, которая называется температурой кипения. Для каждого вещества температура кипения своя.
Слайд 31
В процессе фазового перехода «жидкость – газ» температура
остается постоянной и равной температуре кипения до тех пор,
пока вся система не перейдет из одной фазы в другую.
4: закон испарения: количество тепла Q, необходимое для испарения вещества массой dm, пропорционально этой массе:
. (6.3.5)
Слайд 32
Коэффициент пропорции r в этом выражении, есть константа,
зависящая от вещества системы, называемая удельной теплотой испарения.
Этот закон справедлив и для конденсации, правда с одним отличием: Q в этом случае – тепло выделяемое системой.
Закон испарения можно записать в общем виде:
(6.3.6)
где знак плюс относится к испарению, а знак минус – к конденсации.
Слайд 33
Изменение энтропии в этом процессе можно найти просто,
считая процесс равновесным. И опять это вполне допустимое приближение,
при условии, что разность температур между системой и «поставщиком» тепла невелика, т.е. намного меньше температуры кипения.
Тогда изменение энтропии:
Слайд 34
Из формулы следует, что при испарении энтропия возрастает,
а при конденсации уменьшается.
Слайд 35
Физический смысл этого результата состоит в различии
фазовой области молекулы в жидкости и газе. Хотя в
жидкости и газе каждой молекуле доступна вся область пространства, занятая системой, но сама эта область для жидкости существенно меньше, чем для газа. В жидкости силы притяжения между молекулами удерживают на определенном расстоянии друг от друга, поэтому каждая молекула хотя и имеет возможность свободно мигрировать по области пространства,
Слайд 36
занятой жидкостью, но не имеет возможности «оторваться от
коллектива» остальных молекул: стоит ей оторваться от одной молекулы,
как тут же притягивается другая. Поэтому объем жидкости зависит от её количества и никак не связан с объемом сосуда.
Слайд 37
Молекулы газа ведут себя иначе. У них гораздо
больше свободы, среднее расстояние между ними таково, что силы
притяжения очень малы, и молекулы «замечают друг друга» лишь при столкновениях. В результате газ всегда занимает весь объем сосуда.
Слайд 38
Поэтому при равных температурах фазовая область молекул газа
значительно больше фазовой области молекул жидкости, и энтропия газа
больше энтропии жидкости. Газ, по сравнению с жидкостью, гораздо менее упорядоченная, более хаотичная система и энтропия газа больше энтропии жидкости.
Слайд 39
6.4. Изменения энтропии при обратимых и необратимых процессах
Итак, энтропия – отношение полученной или отданной
системой теплоты в обратимом процессе, к температуре, при которой происходит эта передача.
Энтропия – величина аддитивная, т.е. она равна сумме энтропий всех тел входящих в систему:
Слайд 40
Обратимый цикл Карно
Из п. 5.2
мы знаем, что, в тепловой машине, работающей по принципу
Карно, имеются три тела: холодильник, нагреватель, рабочее тело (газ).
Изменение энтропии газа
так как газ возвращается в исходное состояние.
Слайд 41
Изменение энтропии нагревателя:
(6.4.1)
Для холодильника:
(6.4.2)
А т.к.
,
т.е.
или (6.4.3)
т.е. S – константа.
Это выражение называют равенство Клаузиуса.
Слайд 43
Необратимый цикл
Мы знаем, что
т.е.,
(6.4.4)
Отсюда тогда
Слайд 44
Таким образом
или
(6.4.5)
Это неравенство Клаузиуса.
При любом необратимом процессе в замкнутой системе энтропия возрастает (dS > 0).
Слайд 45
Тогда для замкнутой системы
(6.4.7)
– математическая запись второго начала термодинамики.
Таким образом, для произвольного процесса,
(6.4.6)
где, знак равенства – для обратимого процесса; знак больше для необратимого.
Слайд 46
6.5. Второе начало термодинамики
Термодинамика, это наука о тепловых процессах, о превращении
тепловой энергии. Для описания термодинамических процессов первого начала термодинамики недостаточно. Выражая общий закон сохранения и превращения энергии, первое начало не позволяет определить направление протекания процессов.
Слайд 47
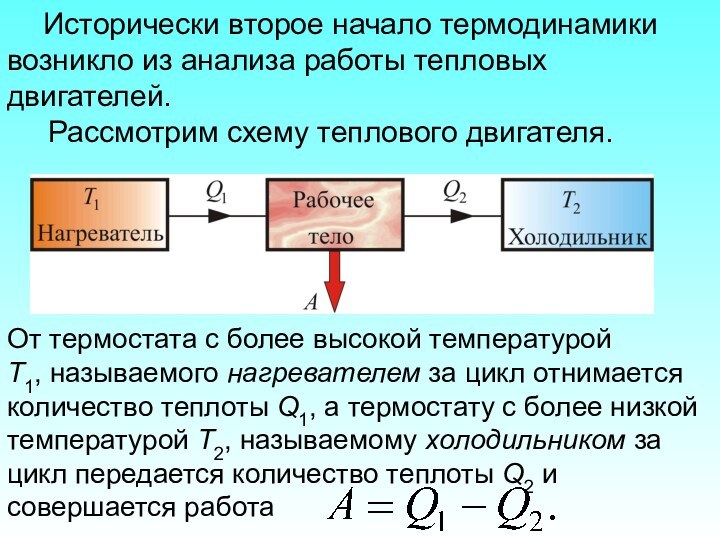
Исторически второе начало термодинамики возникло из анализа работы
тепловых двигателей.
Рассмотрим схему теплового двигателя.
От термостата с более высокой температурой
Т1, называемого нагревателем за цикл отнимается количество теплоты Q1, а термостату с более низкой температурой Т2, называемому холодильником за цикл передается количество теплоты Q2 и совершается работа
Слайд 49
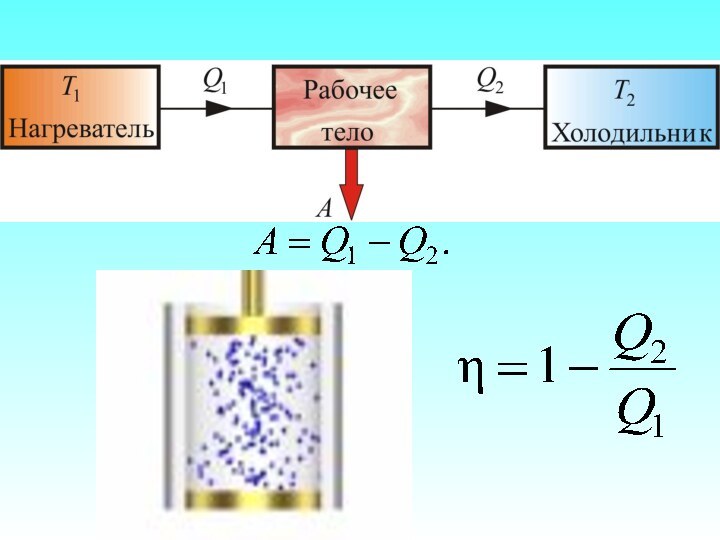
Чтобы термический коэффициент полезного действия теплового двигателя
был , должно
быть выполнено условие , т.е. тепловой двигатель должен иметь один источник теплоты, а это невозможно.
Н. Карно в 1824 г. доказал, что для работы теплового двигателя необходимо не менее двух источников теплоты с различными температурами.
Невозможность создания вечного двигателя второго рода подтверждается вторым началом термодинамики:
Слайд 50
1. Невозможен процесс, единственным результатом
которого является превращение всей теплоты, полученной от нагревателя в
эквивалентную ей работу (формулировка Кельвина)
2. Невозможен вечный двигатель второго рода (формулировка Томпсона-Планка).
3. Невозможен процесс, единственным результатом которого является передача энергии от холодного тела к горячему (формулировка Клаузиуса).
Слайд 51
Математической формулировкой второго начала является выражение
Энтропия замкнутой системы при любых происходивших в ней процессах
не может убывать (или увеличивается или остается неизменной).
Слайд 52
При обратимомном процессе
(6.5.1)
При необратимом процессе, как доказал Клаузиус
(6.5.2)
изменение энтропии больше приведенной теплоты.
Тогда тогда эти выражения можно объединить:
(6.5.3)
Слайд 53
Первое и второе начала термодинамики в объединенной форме
имеют вид:
(6.5.4)
Слайд 54
6.6. Свободная и связанная энергии
Как следует из
первого и второго начала термодинамики в объединенной форме в
обратимом процессе:
Это равенство можно переписать в виде
.
, где F –
разность двух функций состояний, поэтому сама является также функцией состояния. Ее назвали свободной энергией.
Тогда
(6.6.1)
Если тело совершает обратимый изотермический процесс, то
Слайд 56
следовательно свободная энергия есть та работа, которую
могло бы совершить тело в обратимом изотермическом процессе
или, свободная энергия – есть максимальная возможная работа, которую может совершить система, обладая каким-то запасом внутренней энергии.
Слайд 57
Связанная энергия – та часть внутренней
энергии, которая не может быть превращена в работу –
это обесцененная часть внутренней энергии.
При одной и той же температуре, связанная энергия тем больше, чем больше энтропия.
Таким образом, энтропия системы есть мера обесцененности ее энергии (т.е. мера той энергии, которая не может быть превращена в работу).
Внутренняя энергия системы U равна сумме свободной (F) и связанной энергии (TS):
Слайд 58
В термодинамике есть еще понятие – энергетическая потеря
в изолированной системе
(6.6.3)
Слайд 59
При любом необратимом процессе
энтропия увеличивается до того, пока не прекратятся какие-либо процессы,
т.е. пока не станет F = 0.
Это произойдет, при достижении замкнутой системы равновесного состояния, т.е. когда все параметры состояния системы (Р, Т) во всех точках системы станут одинаковыми. Вывести систему из этого равновесного состояния можно только затратив энергию из вне.
На основании этих рассуждений Клаузиус в 1867 г. выдвинул гипотезу о тепловой смерти Вселенной.
Слайд 60
6.7. Статистический смысл энтропии
Посмотрим на
энтропию с другой стороны.
Слайд 61
Макросостояние – это состояние
вещества, характеризуемое его термодинамическими параметрами.
Состояние
же системы, характеризуемое состоянием каждой входящей в систему молекулы, называют микросостоянием.
Так как молекулы движутся хаотически, то имеется много микросостояний, соответствующих одному макросостоянию.
Обозначим W число микросостояний соответствующее данному макросостоянию (как правило W >> 1).
Слайд 62
Термодинамической вероятностью или статистическим
весом макросостояния W называется число микросостояний, осуществляющих данное
макросостояние (или число перестановок одноименных элементов, при которых сохраняется данное макросостояние).
Термодинамическая вероятность W максимальна, когда система находится в равновесном состоянии.
Слайд 63
В состоянии равновесия в термодинамике и вероятность максимальна
и энтропия максимальна.
Из этого можно сделать вывод, что
между ними существует связь. Но!!!
Энтропия S – аддитивная величина:
, т.е. она равна сумме энтропий тел, входящих в систему.
Слайд 64
А вероятность сложного события, есть произведение вероятностей
где W1 – первое состояние; W2 – второе состояние.
Аддитивной величиной является логарифм W:
термодинамическая вероятность или статистический вес.
Слайд 65
Больцман предложил, что
(6.7.1)
где k – коэффициент Больцмана.
С этой точки зрения энтропия выступает, как мера беспорядочности, хаотичности состояния.
Например, в ящике черные и белые шары. Они порознь, есть порядок и W невелика. После встряхивания – шары перемещаются и W – увеличивается и энтропия.
И сколько бы не встряхивать потом ящик, никогда черные шары не соберутся у одной стенки, а белые у другой, хотя эта вероятность не равна нулю.
Слайд 66
Связь между S и W позволяет
несколько иначе сформулировать второе начало термодинамики:
наиболее вероятным изменением
энтропии является ее возрастание.
Слайд 67
Энтропия – вероятностная статистическая величина.
Утверждение о возрастании энтропии потеряло
свою категоричность.
Её увеличение вероятно, но не исключаются флуктуации.
До этих рассуждений Клаузиус в 1867 г. выдвинул гипотезу о тепловой смерти Вселенной (о ней сказано ранее).
Л. Больцман один из первых опроверг эту гипотезу и показал, что закон возрастания энтропии – статистический закон, т.е. возможны отклонения.
Слайд 68
Российские физики Я.Б. Зельдович и И.Д.
Новиков, так же опровергли эту теорию, и показали, что
Р. Клаузиус не учел, что Вселенная не стационарна и в будущем не перейдет к одному состоянию, так как она эволюционирует, остается не статичной.
Энтропия системы – максимальна, при достижении замкнутой системой равновесного состояния.
Слайд 69
6.8. Третье начало термодинамики
Недостатки первого
и второго начал термодинамики в том, что они не
позволяют определить значение энтропии при абсолютном нуле Т = 0º К.
На основании обобщения экспериментальных исследований свойств различных веществ при сверхнизких температурах был установлен закон, устранивший указанный недостаток. Сформулировал его в 1906 г. Нернст и называется он третьим началом термодинамики, или теоремой Нернста.
Нернст Вальтер Фридрих
Герман (1864 – 1941) –
немецкий физик и физико- химик,
один из основоположников
физической химии. Работы в
области термодинамики, физики низких температур, физической химии. Высказал утверждение, что энтропия химически однородного твердого или жидкого тела при абсолютном нуле равна нулю (теорема Нернста). Предсказал эффект «вырождения» газа.
Слайд 71
Согласно Нернсту, изменение энтропии S стремится к нулю
при любых обратимых изотермических процессах, совершаемых между двумя равновесными
состояниями при температурах, приближающихся к абсолютному нулю
(S → 0 при Т → 0).
Нернст сформулировал теорему для изолированных систем, а затем М. Планк распространил ее на случай любых систем, находящихся в термодинамическом равновесии.
Слайд 72
Как первое и второе начала термодинамики, теорема Нернста
может рассматриваться как результат обобщения опытных фактов, поэтому ее
часто называют третьим началом термодинамики:
энтропия любой равновесной системы при абсолютном нуле температуры может быть равна нулю.
Слайд 73
Отсюда следует, что при T 0 интеграл
сходится
на нижнем пределе, т.е.
имеет конечное значение S(0) = const или S(0) = 0, причем равенство нулю рассматривается как наиболее вероятное.
А нулевое значение энтропии (меры беспорядка) соответствует отсутствию теплового движения при абсолютном нуле.
Слайд 74
При T = 0, внутренняя энергия и тепловая
функция системы прекращают зависеть от температуры, кроме того, используя
метод термодинамических функций, можно показать, что при T = 0, от температуры независит коэффициент объемного расширения, термический коэффициент давления и другие параметры системы.
Слайд 75
Согласно классическим представлениям при абсолютном нуле, возможно
непрерывное множество микросостояний системы.
Объяснение теоремы Нернста можно дать
только на основании квантово-механических представлений.
Слайд 76
Третье начало термодинамики иногда формулируют следующим образом:
при
абсолютном нуле температуры любые изменения термодинамической системы происходят без
изменения энтропии:
т.е.
или
Слайд 77
Принцип Нернста бал развит Планком,
предположившим, что при абсолютном нуле температуры энергия системы минимальна
(но не равна нулю).
Тогда можно считать, что при абсолютном нуле система имеет одно квантовое состояние:
значит термодинамическая вероятность W при Т = 0º должна быть равна единице, что недостижимо
(принцип недостижимости абсолютного нуля температуры)