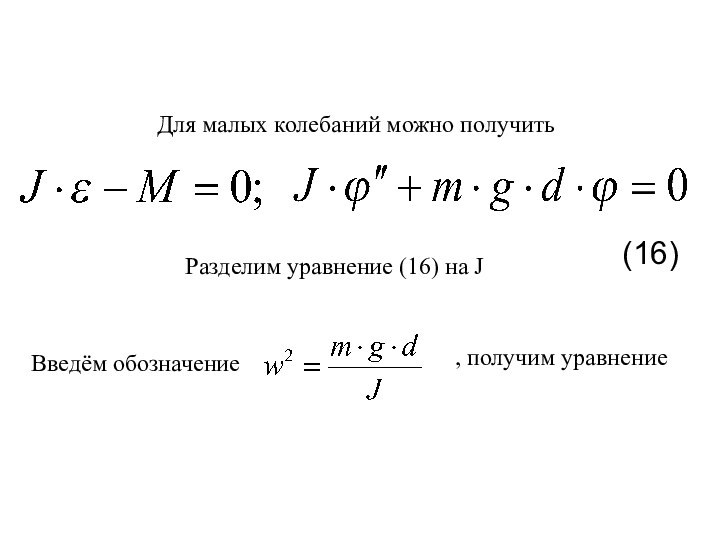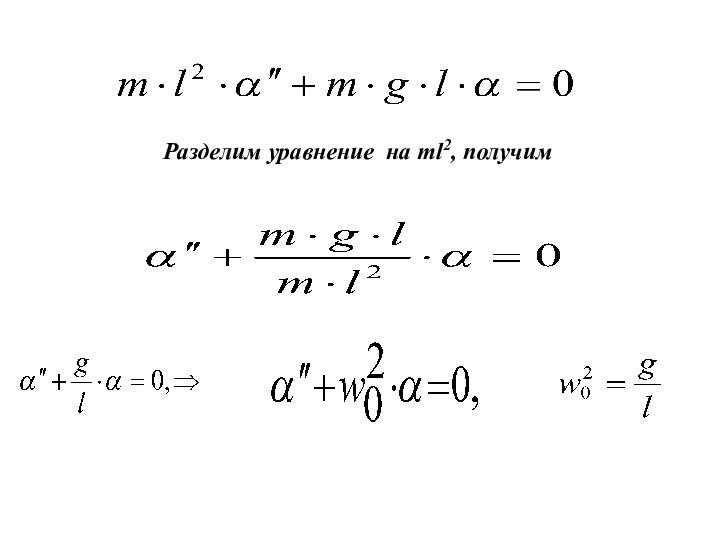и ускорение гармонического колебания
3. Энергия гармонического колебательного движения
4. Свободные колебания. Гармонический осциллятор
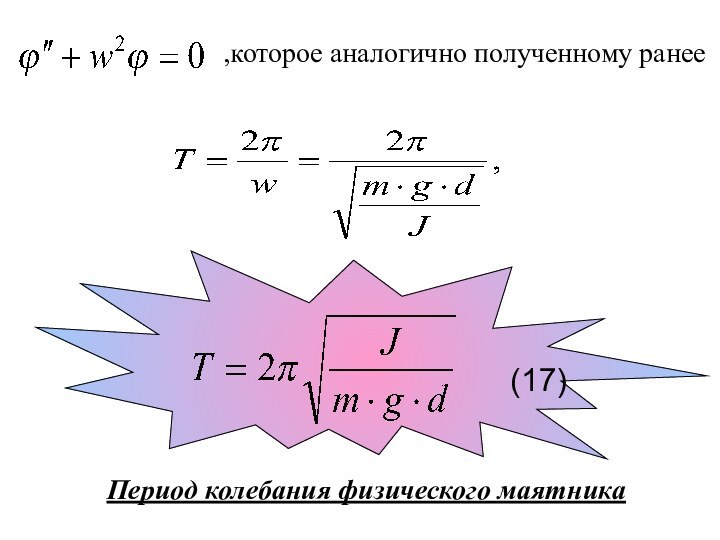
5. Пружинный, математический и физический маятники
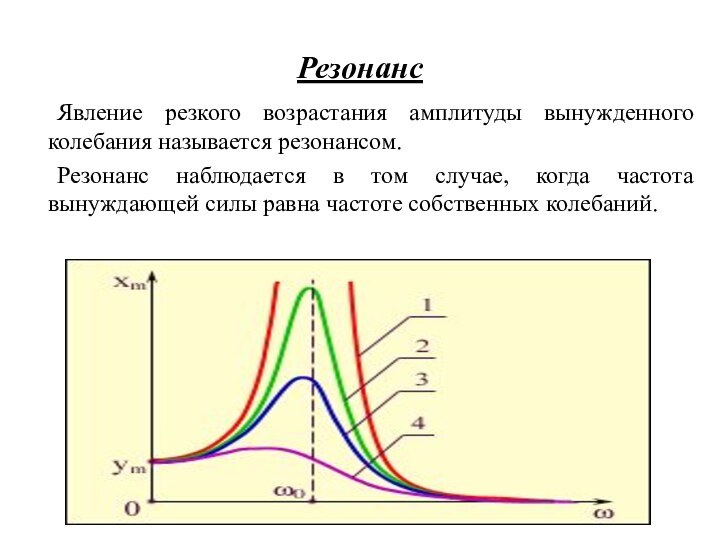
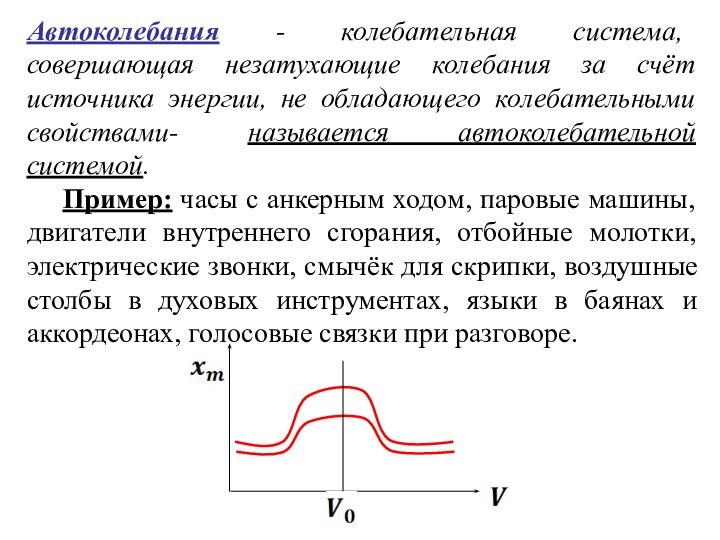
6. Вынужденные колебания. Резонанс. Автоколебания
7. Примеры проявления резонансных явлений в живых организмах
8. Сложение гармонических колебаний, происходящих вдоль одной прямой. Сложение взаимно перпендикулярных колебаний









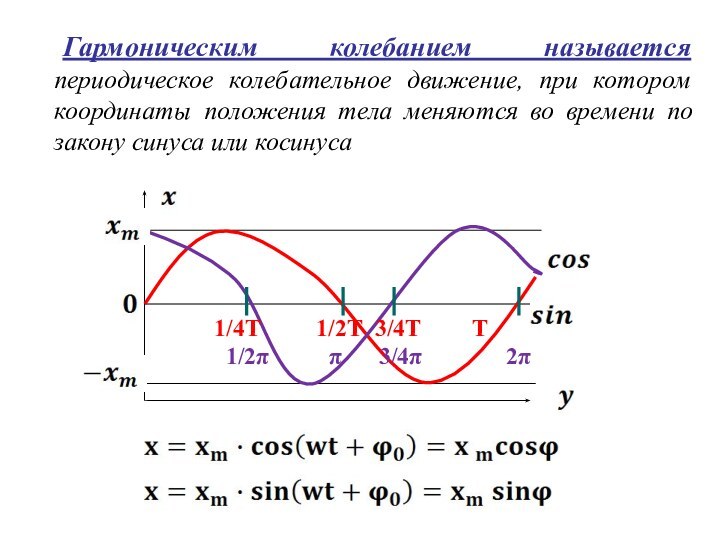

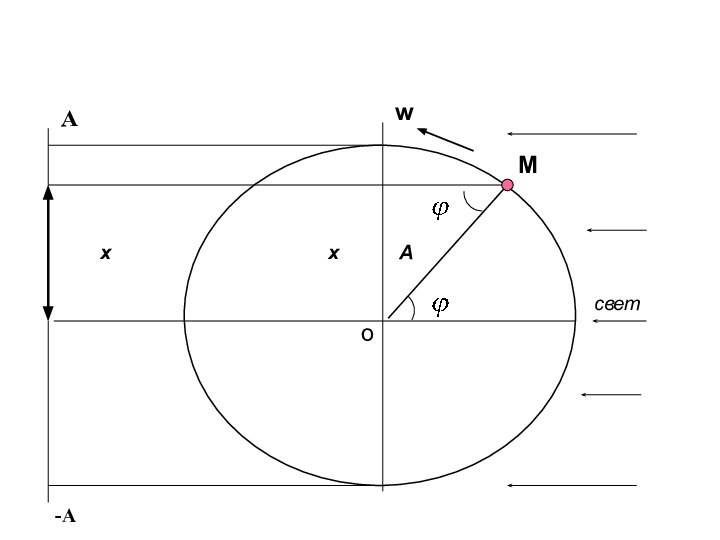



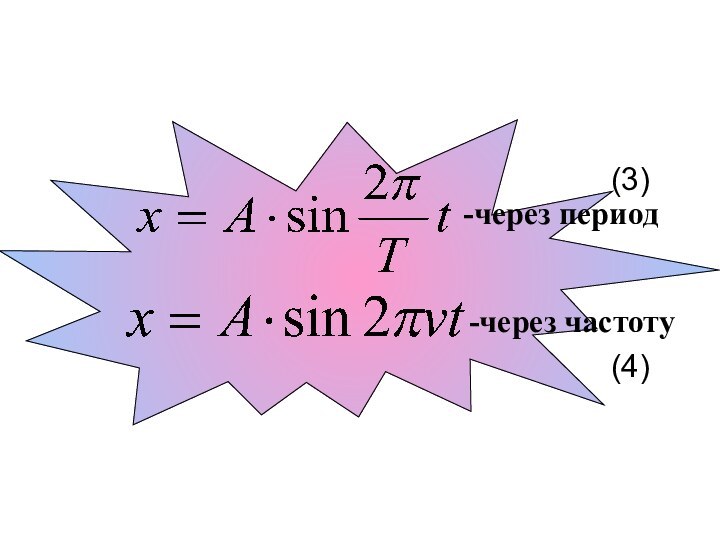

![Гармонические колебания и маятники w – циклическая частота - число полных колебаний за 2π сек,[рад/с] 5.](/img/tmb/12/1194295/3c89d7ebed61489eb5a3fd08e899b6e7-720x.jpg)