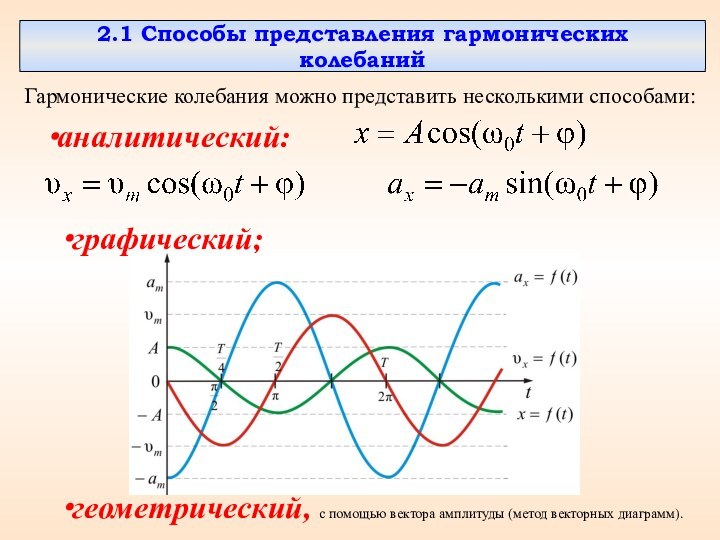
гармонических колебаний
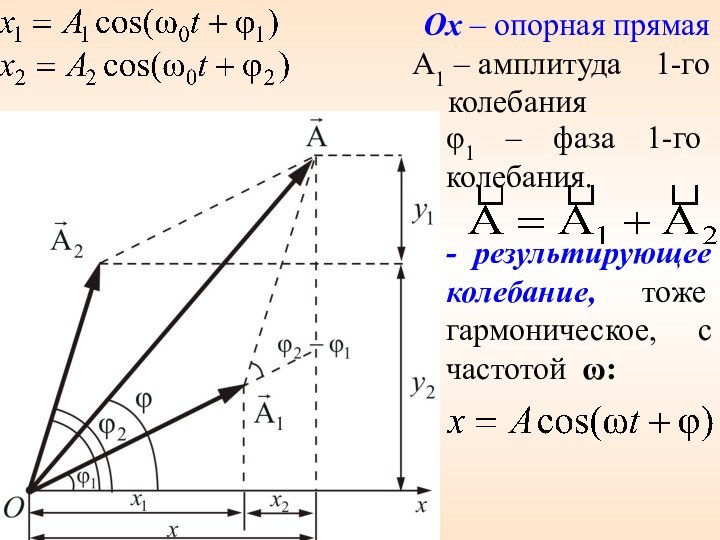
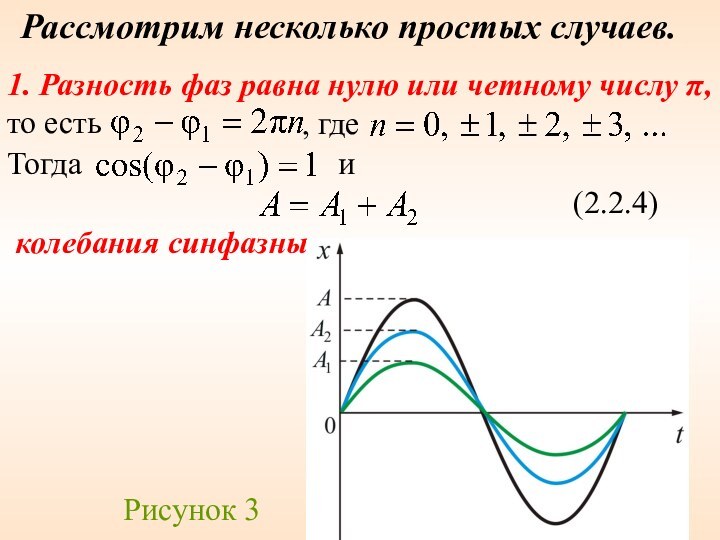
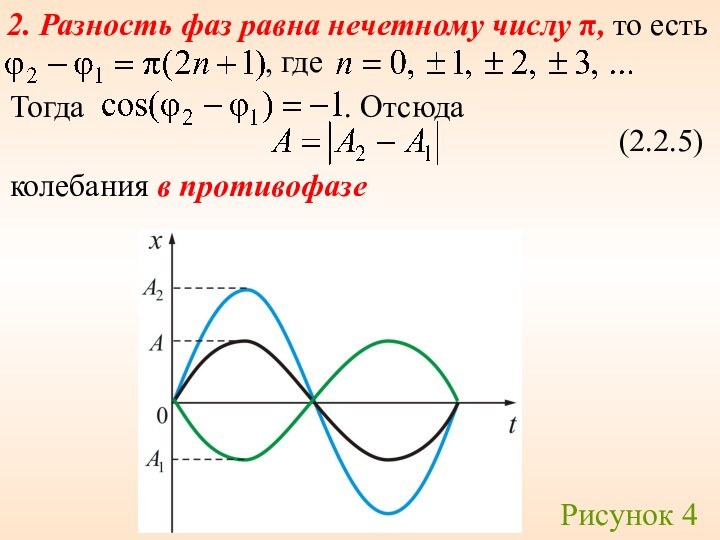
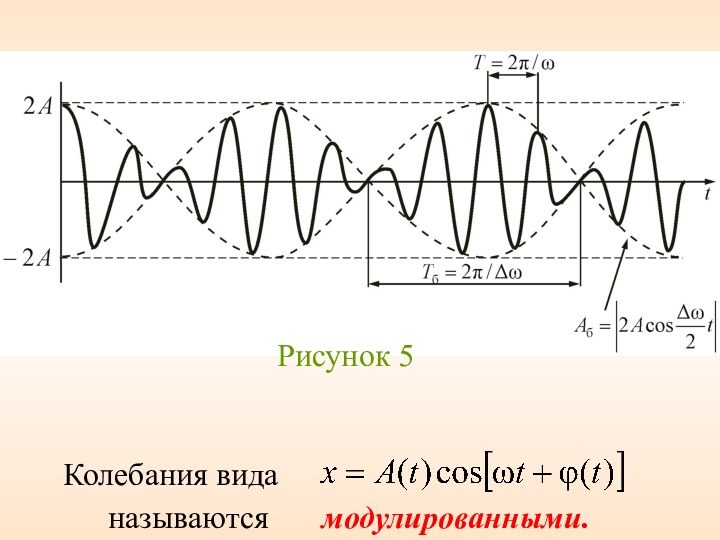
2.2 Сложение гармонических колебаний. Биения
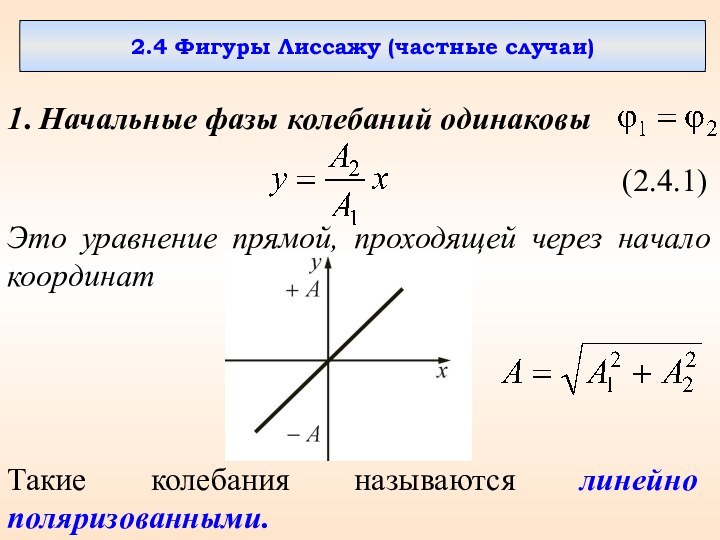
2.3 Сложение взаимно
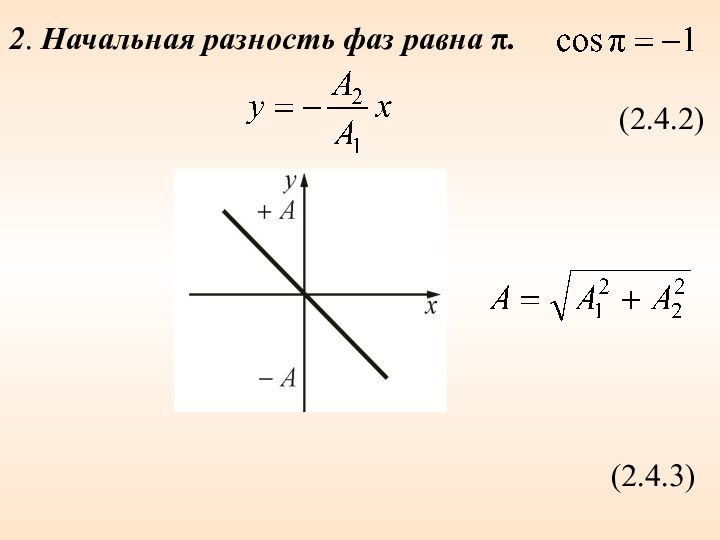
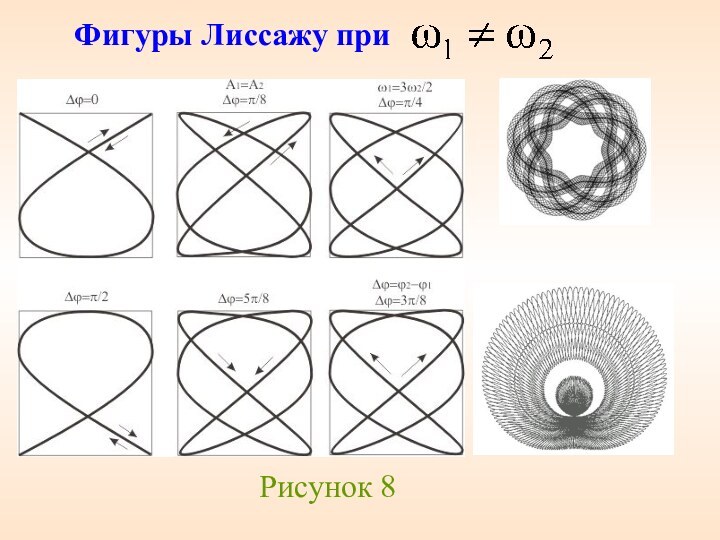
перпендикулярных колебаний2.4 Фигуры Лиссажу (частные случаи)
Сегодня: *