- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Критерии гидродинамического подобия
Содержание
- 2. Но если потоки механически подобны, то сами
- 3. Подобными называют такие потоки жидкости, у которых
- 4. Понятие гидродинамического подобия включает подобие поверхностей, ограничивающих
- 5. Геометрическое подобиеДва потока будут геометрически подобными, если
- 6. Кинематическое подобиеДопустим теперь, что потоки 1 и
- 7. Динамическое подобиеРассмотрим далее какую-либо пару сходственных точек
- 8. Основные коэффициенты подобияСоответственно принятыми в Международной системе
- 9. Производные коэффициентыТак, масштаб скоростей kV = kL
- 10. Критерий РейнольдсаУсловием пропорциональности сил инерции и сил
- 11. Критерий ФрудаУсловием пропорциональности сил инерции и сил
- 12. Соотношения вязкостейПодобие потоков в натуре и модели
- 13. При выполнении условий подобия все безразмерные характеристики
- 14. ЗадачаВ лаборатории исследуется вопрос о гидравлических сопротивлениях,
- 16. Теперь легко находится искомый расход жидкости. Для
- 17. ЗадачаИзучается движение воды при переливе через водосливную
- 18. Так как в натуре и на модели
- 19. Скачать презентацию
- 20. Похожие презентации
Но если потоки механически подобны, то сами уравнения представленные в безразмерном виде, должны быть одинаковыми. Имея это в виду, можно записать уравнения движения (Навье-Стокса) и привести их к безразмерному виду. Для всех динамически подобных потоков они
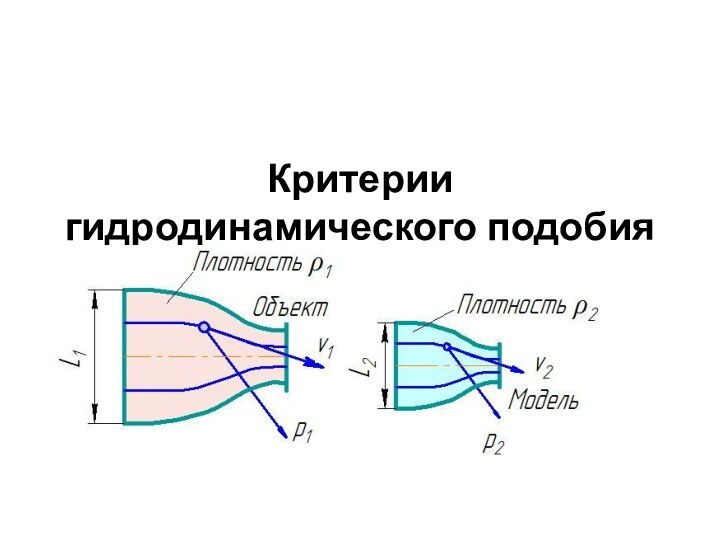

















Слайд 3 Подобными называют такие потоки жидкости, у которых каждая
характеризующая их физическая величина находится для любых сходственных точек
в одинаковом отношении.
Слайд 4
Понятие гидродинамического подобия включает
подобие поверхностей, ограничивающих потоки
(геометрическое подобие);
пропорциональность скоростей в сходственных точках и подобие
траекторий движения сходственных частиц жидкости (кинематическое подобие); пропорциональность сил, действующих на сходственные частицы жидкости, и пропорциональность масс этих частиц (динамическое подобие).
Слайд 5
Геометрическое подобие
Два потока будут геометрически подобными, если любой
линейный размер одного из них можно получить из линейного
размера другого путем умножения на постоянный множитель.Таким образом получаем связь между геометрическими параметрами натуры l1 и модели l2 .
Слайд 6
Кинематическое подобие
Допустим теперь, что потоки 1 и 2
геометрически подобны. Обозначим через v1 и v2 скорости в
их сходственных точках. Если отношениеодинаково
для любой пары сходственных точек, то потоки 1 и 2 будем считать кинематически подобными.
Слайд 7
Динамическое подобие
Рассмотрим далее какую-либо пару сходственных точек и
обозначим силы действующие в этих точках F1 и F2.
Еслиесть величина постоянная для любой пары сходственных точек, то потоки 1 и 2 называются динамически подобными.
Слайд 8
Основные коэффициенты подобия
Соответственно принятыми в Международной системе единиц
основным физическим величинам (длина L время Τ и масса
М) выделяют три основных коэффициента подобия:линейный масштаб kL = L1 / L2 ;
масштаб времени kT = T1 /Т2 ;
и масштаб масс kм =М1/М2.
Слайд 9
Производные коэффициенты
Так, масштаб скоростей kV = kL /
кT ; сил одинаковой физической природы kF = kL
kM / k2T , плотностей kρ = kм /k3L и т.д.Используя выражения масштабов kV и kρ можно получить для масштаба сил kF=kρk2Vk2L ,которая дает общий закон динамического подобия Ньютона:
Его можно представить в форме
Слайд 10
Критерий Рейнольдса
Условием пропорциональности сил инерции и сил вязкостного
трения является одинаковое значение числа Re для потоков в
натуре и модели:где v - характерная (обычно средняя в сечении) скорость;
L - характерный размер (обычно диаметр сечения D);
μ - динамическая вязкость.
Данное условие приводит к соотношению для коэффициентов подобия:
и для скоростей в натуре и модели
Слайд 11
Критерий Фруда
Условием пропорциональности сил инерции и сил тяжести
является одинаковое значение числа Fr:
Так как ускорение свободного падения
g в натуре и модели практически всегда одинаково (масштаб ускорений kg = 1), то данное условие приводит к соотношению для коэффициентов подобияи для скоростей в натуре и модели
Слайд 12
Соотношения вязкостей
Подобие потоков в натуре и модели требует
одновременного выполнения условий для чисел Re и Fr или
условий для коэффициентов подобия. Последнее возможно только тогда, когда масштабы линейных размеров и вязкостей находятся в соотношениииз которого следует, что в модели меньших по сравнению с натурой размеров должна применяться менее вязкая жидкость:
Слайд 13 При выполнении условий подобия все безразмерные характеристики потока,
т.е. безразмерные комбинации различных физических величин (например, коэффициенты сопротивления
ξ, скорости φ, расхода μ и т.д.), имеют в натуре и модели одинаковое численное значение.
Слайд 14
Задача
В лаборатории исследуется вопрос о гидравлических сопротивлениях, которые
будут иметь место в проектируемом водопроводе диаметром d1 =1м.
Исследование ведется на воде. Диаметр лабораторного трубопровода принят равным d2 = 0,1 м. Определить, какой расход Q необходимо пропускать по этому трубопроводу для выполнения условий динамического подобия.Слайд 15
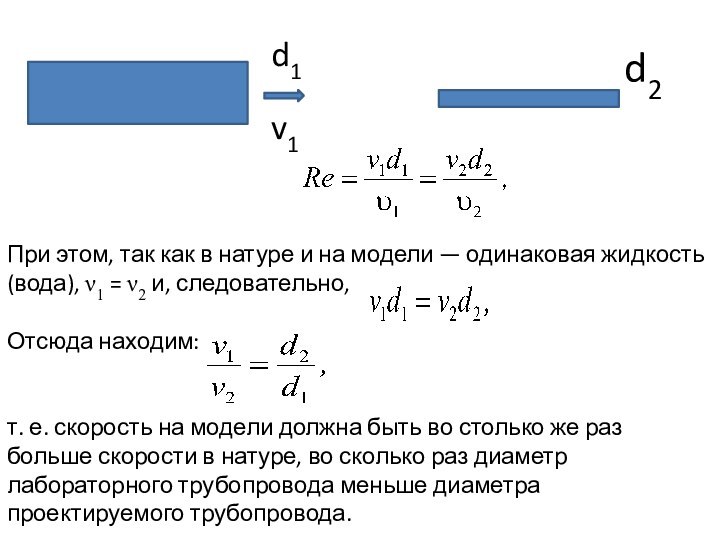
d2
v1
d1
При этом, так как в натуре и на модели — одинаковая жидкость (вода), ν1 = ν2 и, следовательно,
Отсюда находим:
т. е. скорость на модели должна быть во столько же раз больше скорости в натуре, во сколько раз диаметр лабораторного трубопровода меньше диаметра проектируемого трубопровода.
Слайд 16 Теперь легко находится искомый расход жидкости. Для этого
подставим в обычное уравнение расхода вместо v2 и d2
их значения, выраженные через d1 и v1.Таким образом, для подобия наблюдаемых явлений необходимо, чтобы расход на модели Q2 был в десять раз меньше, чем в проектируемом трубопроводе.
Слайд 17
Задача
Изучается движение воды при переливе через водосливную плотину.
Лабораторная модель плотины выполнена в масштабе kL=L1/L2=10, где L1—
геометрические размеры плотины, а L2 — соответственные размеры её модели. Определить, какую скорость движения жидкости необходимо осуществить на модели.Слайд 18 Так как в натуре и на модели движется
одна и та же жидкость (вода), то ν1 =
ν2 , а g1 = g2. При этом закон подобия Рейнольдса получит выражениев то время как закон подобия Фруда будет