Слайд 2
ПЛАН ЛЕКЦИИ
ТЕМА 5
Арнольд И.В. Лексикология современного английского
Классификация
механических передач и их назначение. Передаточное число и передаточное
отношение. Фрикционные передачи. Назначение и особенности фрикционных передач. Расчет фрикционных тел на контактную прочность. Силовые соотношения в цилиндрической фрикционной передаче и расчет ее на прочность.
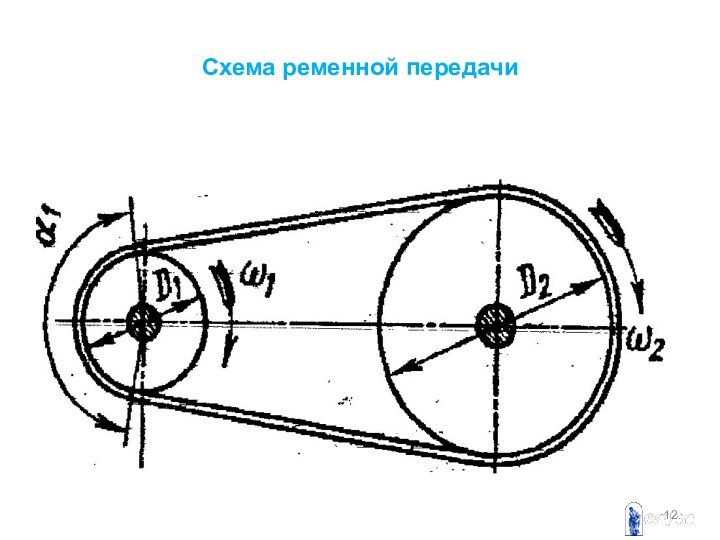
Ременные передачи. Общие сведения. Характеристика передачи и видов ремней. Виды натяжения ремней. Основы теории и расчета ременных передач. Межосевое расстояние, длина ремня, угол наклона ветвей ремня к линии центров, углы обхвата шкивов. Предварительное натяжение ремня, окружное усилие, натяжение в ремне от центробежных сил. Материалы, конструкции и расчет шкивов. Ременные вариаторы.
школа английской лингвистики, 1959. – 312 с.
Слайд 3
Классификация механических передач
Передача вращательного движения производится одним из
следующих способов:
непосредственным соприкосновением двух тел, одно из которых связано
жестко с ведущим, а другое — с ведомым валом;
посредством гибких тел, сцепляющихся с телами, жесткосвязанными с ведущим и ведомым валами.
Первый из этих способов осуществляется в передачах фрикционной, зубчатой и червячной, второй — в передачах ременной и цепной.
Передача вращательного движения может производиться с увеличением или уменьшением угловой скорости вращения, а также без ее изменения.
Слайд 4
Классификация механических передач и их назначение
Передачи по принципу
работы разделяются на:
Передачи зацеплением:
с непосредственным контактом (зубчатые и червячные);
с
гибкой связью (цепные, зубчато-ременные).
Передачи трением (сцеплением трущихся поверхностей):
с непосредственным контактом поверхностей (фрикционные);
с гибкой связью (ременные).
Слайд 5
Передаточное число и передаточное отношение
Отношение угловых скоростей вращения
обоих валов называется передаточным отношением. Передаточное отношение может быть,
следовательно, выражено отношением угловой скорости ведущего вала к угловой скорости ведомого вала или наоборот.
Передаточное отношение в направлении силового потока, т. е. отношение угловой скорости ведущего вала к угловой скорости ведомого, называется передаточным числом.
Слайд 6
Использование материалов презентации
Использование данной презентации, может осуществляться только

при условии соблюдения требований законов РФ об авторском праве
и интеллектуальной собственности, а также с учетом требований настоящего Заявления.
Презентация является собственностью авторов. Разрешается распечатывать копию любой части презентации для личного некоммерческого использования, однако не допускается распечатывать какую-либо часть презентации с любой иной целью или по каким-либо причинам вносить изменения в любую часть презентации. Использование любой части презентации в другом произведении, как в печатной, электронной, так и иной форме, а также использование любой части презентации в другой презентации посредством ссылки или иным образом допускается только после получения письменного согласия авторов.
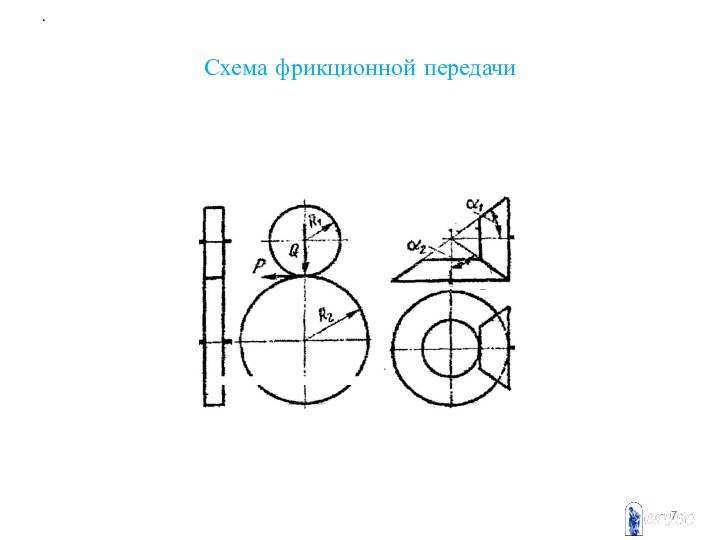
Фрикционные передачи
Передают движение за счёт сил трения (лат. frictio – трение). Простейшие передачи состоят из двух цилиндрических или конических роликов - катков.
Главное условие работы передачи состоит в том, что момент сил трения между катками должен быть больше передаваемого вращающего момента. Передаточное отношение цилиндрической фрикционной передачи определяют как отношение частот вращения или диаметров тел качения.
U = n1/n2=D2/[D1(1-)],
где ε – коэффициент скольжения (0,05 - для передач "всухую"; 0,01 – для передач со смазкой и большими передаточными отношениями).
Слайд 7
Схема фрикционной передачи
.
Слайд 8
Расчет фрикционных передач
Поскольку всё это следствие высоких контактных
напряжений сжатия, то в качестве проектировочного выполняется расчёт по
допускаемым контактным напряжениям . Здесь применяется формула Герца-Беляева, которая, собственно говоря, и была выведена для этого случая. Исходя из допускаемых контактных напряжений, свойств материала и передаваемой мощности определяются диаметры фрикционных колёс:
Поскольку всё это следствие высоких контактных напряжений сжатия, то в качестве проектировочного выполняется расчёт по допускаемым контактным напряжениям [29]. Здесь применяется формула Герца-Беляева, которая, собственно говоря, и была выведена для этого случая. Исходя из допускаемых контактных напряжений, свойств материала и передаваемой мощности определяются диаметры фрикционных колёс
Слайд 9
Фрикционные передачи
Основные требования к материалам фрикционных колёс:
высокая износостойкость
и поверхностная прочность;
высокий коэффициент трения (во избежание больших сил
сжатия);
высокий модуль упругости (чтобы площадка контакта, а значит и потери на трение были малы).
Слайд 10
Достоинства фрикционных передач:
простота тел качения;
равномерность вращения, что удобно
для приборов;
возможность плавного регулирования скорости;
отсутствие мёртвого хода при реверсе
передачи.
Недостатки фрикционных передач:
потребность в прижимных устройствах;
большие нагрузки на валы, т.к. необходимо прижатие дисков;
большие потери на трение;
повреждение катков при пробуксовке;
неточность передаточных отношений из-за пробуксовки.
Слайд 11
Ременные передачи
Являются разновидностью фрикционных
передач, где движение передаётся посредством специального кольцевого замкнутого ремня.
Ременные передачи применяются для привода агрегатов от электродвигателей малой и средней мощности; для привода от маломощных двигателей внутреннего сгорания.
Слайд 13
ОСНОВНЫЕ СЕЧЕНИЯ РЕМНЕЙ
Ремни имеют различные сечения:
а) плоские, прямоугольного
сечения;
б) трапециевидные, клиновые;
в) круглого сечения;
г) поликлиновые.
Слайд 14
Достоинства ременных передач:
передача движения на средние расстояния;
плавность работы и бесшумность;
возможность работы при высоких оборотах;
дешевизна.
Недостатки ременных передач:
большие габариты передачи;
неизбежное проскальзывание ремня;
высокие нагрузки на валы и опоры из-за натяжения ремня;
потребность в натяжных устройствах;
опасность попадания масла на ремень;
малая долговечность при больших скоростях.
Слайд 15
Виды натяжения ремней
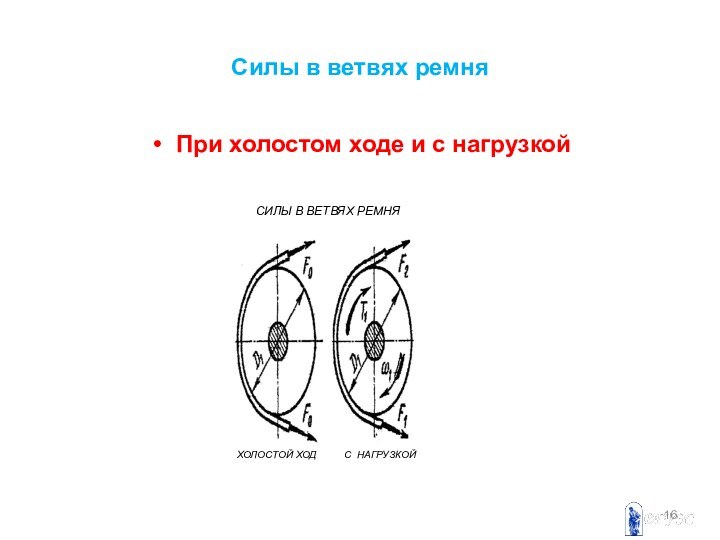
Для создания трения ремень надевают с
предварительным натяжением Fo. В покое или на холостом ходу
ветви ремня натянуты одинаково. При передаче вращающего момента Т1 натяжения в ветвях перераспределяются: ведущая ветвь натягивается до силы F1, а натяжение ведомой ветви уменьшается до F2. Составляя уравнение равновесия моментов относительно оси вращения имеем –T1 + F1D1/2 – F2D2/2 = 0 или F1 – F2 = Ft, где Ft – окружная сила на шкиве Ft = 2T1/D1.
Слайд 16
Силы в ветвях ремня
При холостом ходе и с
нагрузкой
Слайд 17
Общая длина ремня не зависит
от нагрузки , следовательно, суммарное натяжение ветвей остаётся постоянным:
F1 + F2 = 2Fo. Таким образом, получаем систему двух уравнений c тремя неизвестными:
F1 = Fo + Ft/2; F2 = Fo – Ft/2.
Эти уравнения устанавливают изменение натяжения ветвей в зависимости от нагрузки Ft, но не показывают нам тяговую способность передачи, которая связана с силой трения между ремнём и шкивом. Такая связь установлена Л.Эйлером с помощью дифференциального анализа.
Слайд 18
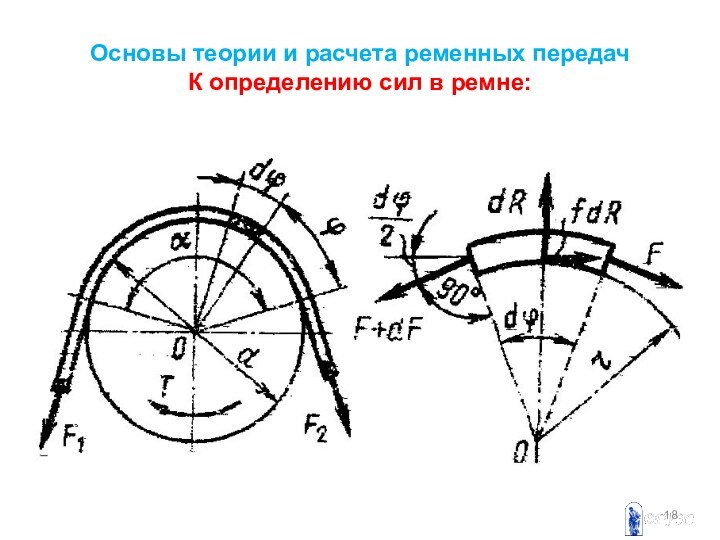
Основы теории и расчета ременных передач
К определению сил
в ремне:
Слайд 19
Рассмотрим элементарный участок ремня dφ.
Для него dR – нормальная реакция шкива на элемент
ремня, fdR – элементарная сила трения. По условию равновесия суммы моментов
rF + rfdR – r(F + dF) = 0.
Сумма горизонтальных проекций сил:
dR – Fsin(dφ/2) – (F+dF)sin(dφ/2) = 0.
Отбрасывая члены второго порядка малости и помня, что синус бесконечно малого угла равен самому углу, Эйлер получил простейшее дифференциальное уравнение: dF/F = f dφ.
Слайд 20
Интегрируя левую часть этого уравнения в пределах от
F1 до F2, а правую часть в пределах
угла обхвата ремня получаем: F1 = F2 e fα.
Теперь стало возможным найти все неизвестные силы в ветвях ремня:
F1 = Ft efα /(efα-1); F2 = Ft /(efα-1);
Fo = Ft (efα+1) / 2(efα-1 ).
При круговом движении ремня на него действует центробежная сила
Fv = ρSv2, где S - площадь сечения ремня.
Слайд 21
Напряжения в ремне
В ремне
действуют следующие напряжения:
предварительное напряжение (от силы натяжения Fo)
o = Fo / S;
"полезное" напряжение (от полезной нагрузки Ft) п = Ft / S;
напряжение изгиба и = δ Е / D
(δ – толщина ремня, Е – модуль упругости ремня, D – диаметр шкива);
напряжения от центробежных сил
v = Fv / S.
Слайд 22
Наибольшее суммарное напряжение возникает в сечении ремня в
месте его набегания на малый шкив
max = o + п + и + v.
При этом напряжения изгиба не влияют на тяговую способность передачи, однако являются главной причиной усталостного разрушения ремня.
Слайд 23
Силы натяжения ветвей ремня
Силы натяжения ветвей ремня (кроме
центробежных) воспринимаются опорами вала. Равнодействующая нагрузка на опору
Fr ≈ 2 Focos(β/2).
Обычно эта радиальная нагрузка на опору в 2 … 3 раза больше передаваемой ремнём вращающей силы.
Слайд 24
Порядок проектного расчета плоскоременной передачи
1.Выбирают тип ремня.
2.Определяют диаметр
малого шкива D1=(110…130)(N/n)1/3, где N–мощность, КВТ, n–частота
вращения, об/мин.
3.Выбирают межосевое расстояние, подходящее для конструкции машины 2(D1+D2) ≤a≤15м.
4.Проверяют угол обхвата на малом шкиве:
α1=180о-57о(D2-D1)/a, рекомендуется [α1]≥150о, при необходимости на ведомой нити ремня применяют натяжной ролик, который позволяет даже при малых межосевых расстояниях получить угол обхвата более 180о.
Слайд 25
5.По передаваемой мощности N и скорости v ремня
определяют ширину b≥N/(vz[p]) и площадь ремня F≥N/(v[k]), где [p]
–допускаемая нагрузка на 1мм ширины прокладки, [k] – допускаемая нагрузка на единицу площади сечения ремня.
6.Подбирают требуемый ремень по ГОСТ .
7.Проверяют ресурс передачи
N=3600vzшT.
8.Вычисляют силы, действующие на валы передачи
FR= Focos(β/2).
Слайд 26
Порядок проектного расчета клиноременной передачи
1.Выбирают по ГОСТ профиль
ремня. Большие размеры в таблицах ГОСТ соответствуют тихоходным, а
меньшие – быстроходным передачам.
2.Определяют диаметр малого шкива.
3.Выбирают межосевое расстояние, подходящее для конструкции машины 0,55(DM+Dб)+h ≤ a ≤ 2(D1+D2), где h – высота сечения ремня.
4.Находят длину ремня и округляют её до ближайшего стандартного значения.
5.Проверяют частоту пробегов ремня и если она выше допустимой, то увеличивают диаметры шкивов или длину ремня.
Слайд 27
6. Окончательно уточняют межосевое расстояние.
7. Определяют угол обхвата
на малом шкиве
α1 = 180о-57о(D2-D1)/a, рекомендуется [α1] ≥
120о.
8. По тяговой способности определяют число ремней.
9. При необходимости проверяют ресурс.
10. Вычисляют силы, действующие на валы передачи.
Слайд 29
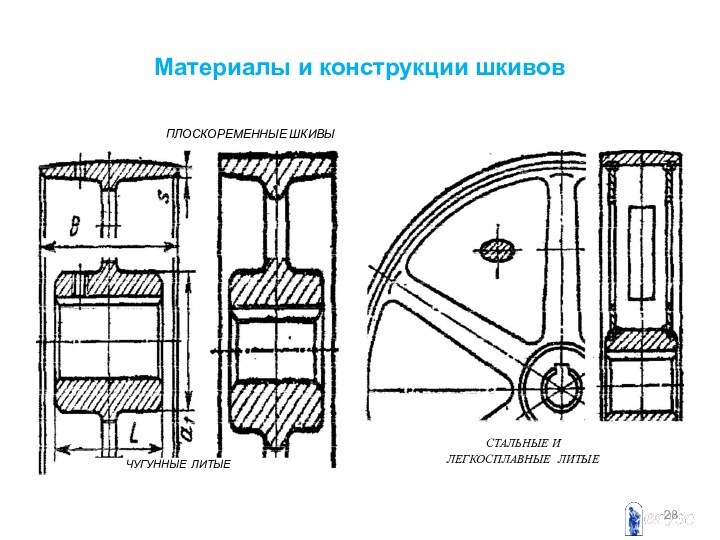
Шкивы плоскоременных передач имеют: обод, несущий ремень, ступицу,
сажаемую на вал и спицы или диск, соединяющий обод
и ступицу.
Шкивы обычно изготавливают чугунными литыми, стальными, сварными или сборными, литыми из лёгких сплавов и пластмасс. Диаметры шкивов определяют из расчёта ременной передачи, а потом округляют до ближайшего значения из ряда R40 . Ширину шкива выбирают в зависимости от ширины ремня.
Слайд 30
Чугунные шкивы примеряются при скоростях до
30 -
45 м/с.
Стальные сварные шкивы применяются при скоростях 60
– 80 м/с.
Шкивы из легких сплавов перспективны для быстроходных передач до 100 м/c.
Шкивы малых диаметров до 350 мм имеют сплошные диски.
Шкивы больших диаметров – ступицы переменного сечения.
Слайд 31
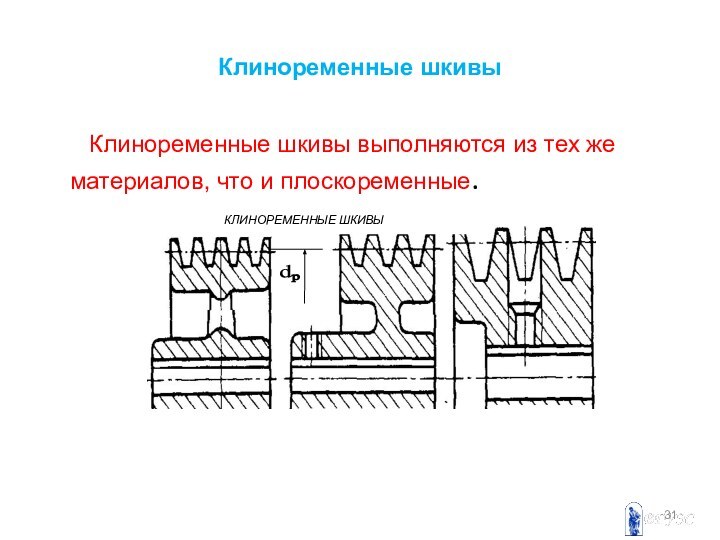
Клиноременные шкивы
Клиноременные шкивы выполняются
из тех же материалов, что и
плоскоременные.
Слайд 32
Материалы клиновых ремней
Материалы клиновых ремней в основном те
же, что и для плоских. Выполняются прорезиненные ремни
с тканевой обёрткой для большего трения, кордотканевые (многослойный корд) и кордошнуровые ремни (шнур, намотанный по винтовой линии), ремни с несущим слоем из двух канатиков. Иногда для уменьшения изгибных напряжений применяют гофры на внутренней и наружных поверхностях ремня. Клиновые ремни выпускают бесконечными (кольца). Угол клина ремня 40о.
Слайд 33
Ременные вариаторы
Ременные вариаторы получили широкое применение (сельхозмашины, станки
и др.) благодаря простой конструкции и невысокой стоимости.
Промышленность
выпускает мотор-вариаторы и автономные вариаторы. Их недостатки обусловлены значительными габаритами и сравнительно небольшим диапазоном регулирования.
Слайд 34
В вариаторах с плоским ремнем скорость регулируется в
узких пределах" за счет осевого перемещения ремня.
Они имеют
невысокую тяговую способность, большие габариты, поэтому применяются редко.
Клиноременные вариаторы более компактны, надежны в эксплуатации и имеют больший диапазон регулирования.
Слайд 35
На рис. 1 показаны типичные схемы вариаторов, состоящих
из двух раздвижных конусов {раздвижных шкивов) и клинового ремня
(обычного или специального, вариаторного).
Скорость регулируют путем изменения диаметров одного (рис. 1, а) или одновременно двух (рис. 1, б) шкивов при осевом смещении конических дисков.
Если в передаче регулируется один шкив, то при этом принудительно изменяется межосевое расстояние.
Слайд 36
Схемы клиноременных вариаторов (рис1,а,б)




















![Механические передачи трением 5.По передаваемой мощности N и скорости v ремня определяют ширину b≥N/(vz[p]) и](/img/tmb/11/1089616/1ea3c0919f52527d2bfdbf35ad897fd3-720x.jpg)