при котором взаимодействие длится очень короткое время.
Центральный удар –
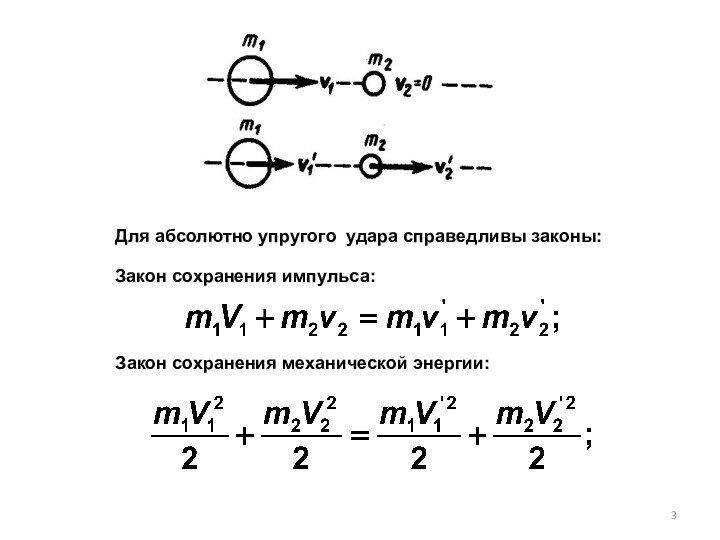
такой, если тела до удара движутся вдоль прямой, проходящей через их центры масс.Определения:
Абсолютно упругий удар — столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию.
Абсолютно неупругий удар — столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое.
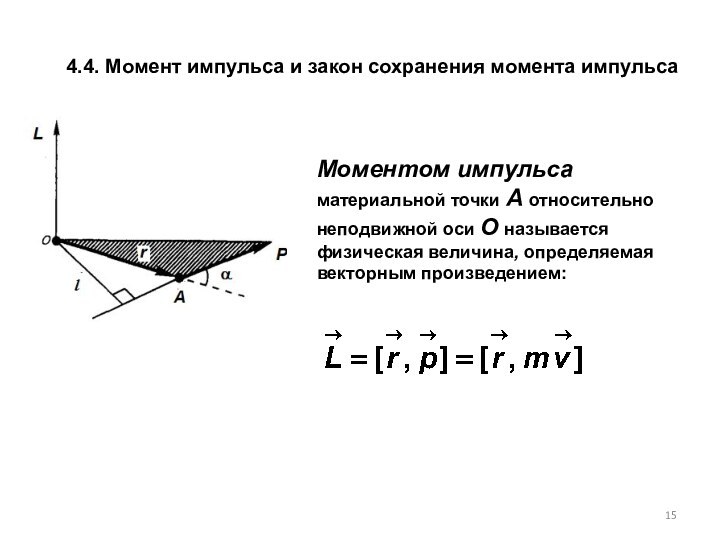
3.3. Соударения тел