Слайд 2
Развитие представлений о природе света
В конце XVII века
возникли две теории света: корпускулярная (И. Ньютон) и волновая (Р. Гук
и Х. Гюйгенс).
Согласно корпускулярной теории, свет представляет собой поток частиц (корпускул), испускаемых светящимися телами. Ньютон считал, что движение световых корпускул подчиняется законам механики. Так, отражение света понималось аналогично отражению упругого шарика от плоскости. Преломление света объяснялось изменением скорости корпускул при переходе из одной среды в другую. Для случая преломления света на границе вакуум–среда корпускулярная теория приводила к следующему виду закона преломления:
где c – скорость света в вакууме, υ – скорость распространения света в среде. Так как n > 1, из корпускулярной теории следовало, что скорость света в средах должна быть больше скорости света в вакууме.
Слайд 3
Волновая теория, в отличие от корпускулярной, рассматривала свет
как волновой процесс, подобный механическим волнам. В основу волновой
теории был положен принцип Гюйгенса, согласно которому каждая точка, до которой доходит волна, становится центром вторичных волн, а огибающая этих волн дает положение волнового фронта в следующий момент времени. С помощью принципа Гюйгенса были объяснены законы отражения и преломления. Рис. дает представление о построениях Гюйгенса для определения направления распространения волны, преломленной на границе двух прозрачных сред.
Слайд 4
Важнейшую роль в выяснении природы света сыграло опытное
определение его скорости.
Современная лазерная техника позволяет
измерять скорость света с очень высокой точностью на основе независимых измерений длины волны λ и частоты света ν (c = λ · ν). Таким путем было найдено значение
превосходящее по точности все ранее полученные значения более чем на два порядка.
Слайд 5
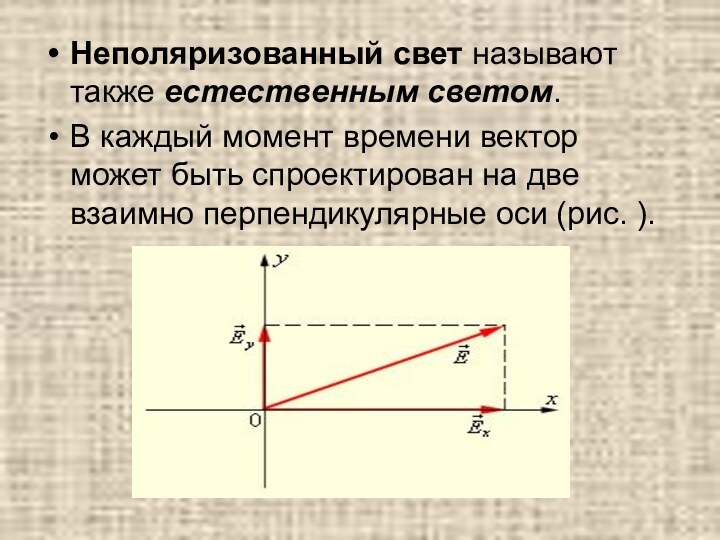
под светом понимают не только видимый свет, но
и примыкающие к нему широкие диапазоны спектра электромагнитного излучения
– инфракрасный ИК и ультрафиолетовый УФ. По своим физическим свойством свет принципиально неотличим от электромагнитного излучения других диапазонов – различные участки спектра отличаются друг от друга только длиной волны λ и частотой ν.
Рис. дает представление о шкале электромагнитных волн.
Слайд 6
Для измерения длин волн в оптическом диапазоне используются
единицы длины 1 нанометр (нм) и 1 микрометр (мкм):
1 нм = 10–9 м = 10–7 см = 10–3 мкм.
Видимый свет занимает диапазон приблизительно от 400 нм до 780 нм или от 0,40 мкм до 0,78 мкм.
Слайд 7
Интерференция световых волн
Интерференция – одно из ярких
проявлений волновой природы света.
Первый эксперимент по наблюдение интерференции света
в лабораторных условиях принадлежит И. Ньютону. Он наблюдал интерференционную картину, возникающую при отражении света в тонкой воздушной прослойке между плоской стеклянной пластиной и плосковыпуклой линзой большого радиуса кривизны. Интерференционная картина имела вид концентрических колец, получивших название колец Ньютона.
Слайд 8
Наблюдение колец Ньютона. Интерференция возникает при сложении волн,
отразившихся от двух сторон воздушной прослойки. «Лучи» 1 и
2 – направления распространения волн; h – толщина воздушного зазора.
Слайд 9
Исторически первым интерференционным опытом, получившим объяснение на основе
волновой теории света, явился опыт Юнга (1802 г.)
Слайд 10
Монохроматическая волна, распространяющаяся в направлении радиус-вектора , записывается
в виде
E = a cos (ωt – kr),где a – амплитуда волны,
k = 2π / λ – волновое число, λ – длина волны, ω = 2πν – круговая частота. В оптических задачах под E следует понимать модуль вектора напряженности электрического поля волны. При сложении двух волн в точке P результирующее колебание также происходит на частоте ω и имеет некоторую амплитуду A и фазу φ:
E = a1 · cos (ωt – kr1) + a2 · cos (ωt – kr2) = A · cos (ωt – φ).
Слайд 11
Физическую величину, равную квадрату амплитуды электрического поля волны,
принято называть интенсивностью: I = A2.
Несложные тригонометрические преобразования приводят к следующему
выражению для интенсивности результирующего колебания в точке P:
(*)
где Δ = r2 – r1 – так называемая разность хода
Слайд 12
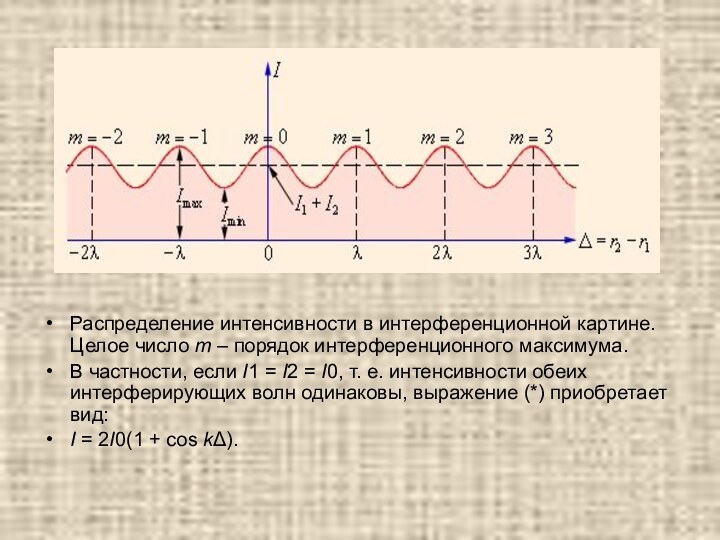
Распределение интенсивности в интерференционной картине. Целое число m
– порядок интерференционного максимума.
В частности, если I1 = I2 = I0, т. е.
интенсивности обеих интерферирующих волн одинаковы, выражение (*) приобретает вид:
I = 2I0(1 + cos kΔ).
Слайд 13
Проблема когерентности волн.
Реальные световые

волны не являются строго монохроматическими. В силу фундаментальных физических
причин излучение всегда имеет статистический характер. Атомы светового источника излучают независимо друг от друга в случайные моменты времени, и излучение каждого атома длится очень короткое время (τ ≤ 10–8 с).
Фаза волны, излучаемой реальным источником света, остается приблизительно постоянной только на интервалах времени порядка τ. Отдельные «обрывки» излучения длительности τ называются цугами. Цуги имеют пространственную длину, равную cτ, где c – скорость света. Колебания в разных цугах не согласованы между собой. Таким образом, реальная световая волна представляет собой последовательность волновых цугов с беспорядочно меняющейся фазой. Принято говорить, что колебания в разных цугах некогерентны. Интервал времени τ, в течении которого фаза колебаний остается приблизительно постоянной, называют временем когерентности.
Интерференция может возникнуть только при сложении когерентных колебаний. Волны, создающие в точке наблюдения когерентные колебания, также называются когерентными. Волны от двух независимых источников некогерентны и не могут дать интерференции.
Слайд 14
Дифракция света
Дифракцией света называется явление отклонения света
от прямолинейного направления распространения при прохождении вблизи препятствий.
дифракционная
картина – система чередующихся светлых и темных колец.
Слайд 15
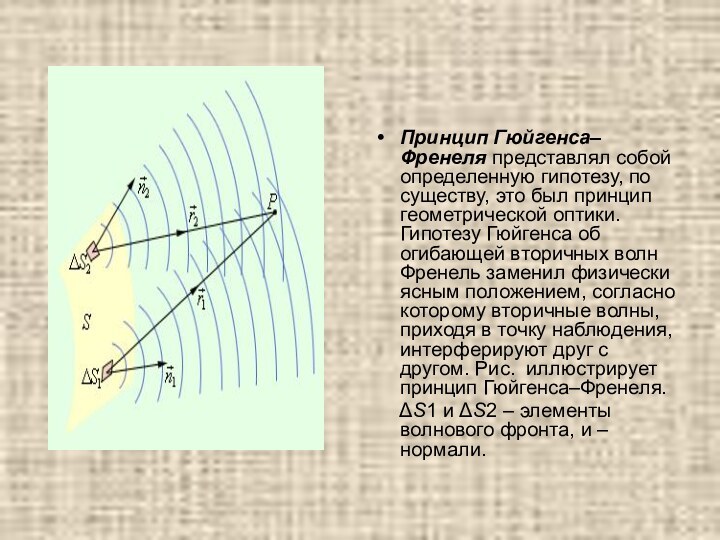
Принцип Гюйгенса–Френеля представлял собой определенную гипотезу, по существу,
это был принцип геометрической оптики. Гипотезу Гюйгенса об огибающей
вторичных волн Френель заменил физически ясным положением, согласно которому вторичные волны, приходя в точку наблюдения, интерферируют друг с другом. Рис. иллюстрирует принцип Гюйгенса–Френеля.
ΔS1 и ΔS2 – элементы волнового фронта, и – нормали.
Слайд 16
Дифракция плоской волны на экране с круглым отверстием
Слайд 17
Если смотреть на волновую поверхность из точки P,
то границы зон Френеля будут представлять собой концентрические окружности.
Радиусы ρm зон Френеля:
Слайд 18
амплитуда колебаний, вызываемых некоторой зоной, равна среднему арифметическому
из амплитуд колебаний, вызываемых двумя соседними зонами, т. е.
если
отверстие в непрозрачном экране оставляет открытой только одну зону Френеля, то амплитуда колебаний в точке наблюдения возрастает в 2 раза (а интенсивность в 4 раза) по сравнению с действием невозмущенной волны. Если открыть две зоны, то амплитуда колебаний обращается в нуль. Если изготовить непрозрачный экран, который оставлял бы открытыми только несколько нечетных (или только несколько четных) зон, то амплитуда колебаний резко возрастает. Такие пластинки, обладающие свойством фокусировать свет, называются зонными пластинками.
Слайд 19
Дифракционный предел разрешения оптических инструментов
Никакая оптическая система
не может дать точечного изображения. В случае дифракции Фраунгофера
на круглом отверстии диаметра D дифракционное изображение состоит из центрального светлого пятна (диск Эйри), на которое приходится приблизительно 85 % энергии света, и окружающих его светлых и темных колец. Это дифракционное пятно и принимается за изображение точечного источника. Радиус центрального пятна в фокальной плоскости линзы равен
Слайд 20
Дифракционное изображение точечного источника (дифракция на круглом отверстии).
В центральное пятно попадает приблизительно 85 % энергии света.
Слайд 21
Разрешающая способность микроскопа. С помощью микроскопа наблюдают близко
расположенные объекты, поэтому его разрешающаяся способность характеризуется не угловым,
а линейным расстоянием между двумя близкими точками, которые еще могут восприниматься раздельно. Наблюдаемый объект располагается вблизи переднего фокуса объектива. Часто пространство перед объективом заполняется специальной прозрачной жидкостью – иммерсией.
Слайд 22
Впервые предел разрешения объектива микроскопа был определен немецким
физиком Г. Гельмгольцем (1874 г.). Формула Гельмгольца имеет вид:
Здесь λ –
длина волны, n – показатель преломления иммерсионной жидкости, α – так называемый апертурный угол (рис. ). Величина n sin α называется числовой апертурой
Слайд 23
Спектральные приборы. Дифракционная решетка
Совокупность монохроматических компонент в
излучении называется спектром. Белый свет имеет непрерывный спектр, излучение
источников, в которых свет испускается атомами вещества, имеет дискретный спектр. Приборы, с помощью которых исследуются спектры излучения источников, называются спектральными приборами.
Для разложения излучения в спектр в простейшем спектральном приборе используется призма (рис. ). Действие призмы основано на явлении дисперсии, то есть зависимости показателя преломления n вещества от длины волны света λ.
Слайд 24
В спектральных приборах высокого класса вместо призм применяются
дифракционные решетки. Решетки представляют собой периодические структуры, выгравированные специальной
делительной машиной на поверхности стеклянной или металлической пластинки.
Слайд 26
Для того, чтобы в точке P наблюдался интерференционный
максимум, разность хода Δ между волнами, испущенными соседними щелями,
должна быть равна целому числу длин волн:
Δ = d sin θm = mλ (m = 0, ±1, ±2, ...).Здесь d – период решетки, m – целое число, которое называется порядком дифракционного максимума. В тех точках экрана, для которых это условие выполнено, располагаются так называемые главные максимумы дифракционной картины.
В фокальной плоскости линзы расстояние ym от максимума нулевого порядка (m = 0) до максимума m-го порядка при малых углах дифракции равно
где F – фокусное расстояние.
Слайд 27
Одной из важнейших характеристик дифракционной решетки является ее
разрешающая способность, характеризующая возможность разделения с помощью данной решетки
двух близких спектральных линий с длинами волн λ и λ + Δλ. Спектральной разрешающей способностью R называется отношение длины волны λ к минимальному возможному значению Δλ, то есть
оценка разрешающей силы решетки:
Слайд 28
Поляризация света
Прохождение света через кристалл исландского шпата
(двойное лучепреломление). Если кристалл поворачивать относительно направления первоначального луча,
что поворачиваются оба луча, прошедшие через кристалл.
Слайд 29
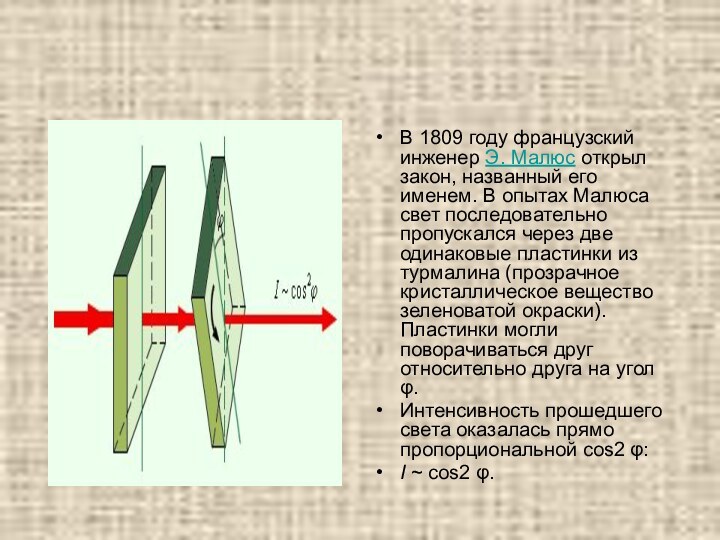
В 1809 году французский инженер Э. Малюс открыл закон, названный
его именем. В опытах Малюса свет последовательно пропускался через
две одинаковые пластинки из турмалина (прозрачное кристаллическое вещество зеленоватой окраски). Пластинки могли поворачиваться друг относительно друга на угол φ.
Интенсивность прошедшего света оказалась прямо пропорциональной cos2 φ:
I ~ cos2 φ.