Презентация на тему Магнитное поле и его характеристики

поля является то, что оно действует только на движущиеся

в этом поле электрические заряды

магнитной индукции В. Его используют также в качестве силовой

характеристикой, численно приравнивая максимальному вращающему моменту, действующему на рамку с магнитным моментом, равным единице. В качестве единицы измерения магнитной индукции в системе СИ принимают тесла (Тл).

можно изображать с помощью линий магнитной индукции – линий,

касательные к которым в каждой точке совпадают с направлением вектора В. Их направление задается правилом правого винта: головка винта, ввинчиваемого по направлению тока, вращается в направлении линий магнитной индукции. Линии магнитной индукции всегда замкнуты и охватывают проводники с током.

обусловленные движением электронов в атомах и молекулах. Эти микротоки

создают свое магнитное поле и могут поворачиваться в магнитных полях макротоков. Вектор магнитной индукции В характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками. Магнитное поле макротоков описывается вектором напряженности Н. Для однородной изотропной среды вектор магнитной индукции связан с вектором напряженности следующим соотношением:


где μ0 – магнитная постоянная (μ0 = 4π×10-7 Гн/м),
μ – безразмерная величина – магнитная проницаемость среды, показывающая, во сколько раз магнитное поле макротоков Н усиливается за счет поля микротоков среды.
В СИ напряженность магнитного поля измеряют в ампер на метр (А/м).

с помощью которого рассчитываются магнитные поля, в векторной и

скалярной формах имеет вид соответственно:

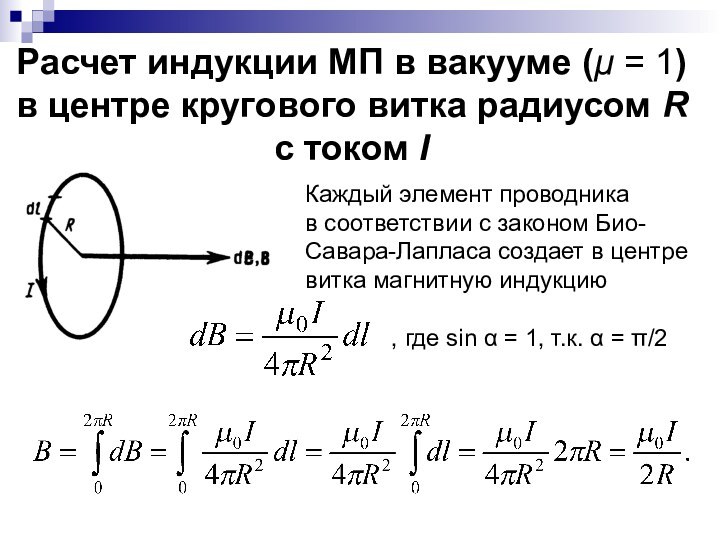
где dB – магнитная индукция, создаваемая элементарным проводником dl, по которому течет ток I, в точке А; α – угол между направлением тока в проводнике и радиус-вектором r. Выбор направления (от нас) вектора индукции объясняется выше.

R от конечного (длиной l) или бесконечного прямого проводника

с током I (рис. выше)

Для бесконечного провода
В результате для бесконечного прямого провода с током I имеем

кругового витка радиусом R с током I
Каждый элемент проводника

в соответствии с законом Био-Савара-Лапласа создает в центре витка магнитную индукцию

, где sin α = 1, т.к. α = π/2

восстановленном из центра проводящего кольца радиусом R с током

I, на расстоянии а от плоскости кольца

В силу симметрии вдоль направления х интеграл

Согласно построению АЕ равен половине dBp, откуда


тогда