Слайд 2
В зависимости от времени теплообмен может быть: стационарным,

если температурное поле меняется во времени; стационарно-периодическим (тепловолны), если
имеет место периодическое изменение температурного поля.
В зависимости от характера теплового движения различают следующие виды теплообмена:
- теплопроводность - молекулярный перенос теплоты в среде с не-одноодным распределением температуры посредством теплового движения микрочастиц.
- конвекция - перенос теплоты в среде с неоднородным распреде-
температуры при движении среды.
Теплообмен излучением - теплообмен, включающий переход Внутренней энергии тела (вещества) в энергию излучения, перенос излучения, преобразование энергии излучения во внутреннюю энергию другого тела (вещества).
На практике также имеют место следующие процессы. Конвективный теплообмен - теплообмен при совместном проте-кании молекулярног и конвективного переноса теплоты (теплопро-водности и конвекции),
Теплоотдача (конвективная теплоотдача) - конвективный теп-лообмен между движущейся средой и поверхностью ее раздела с дру-гой средой (твердым телом, жидкостью или газом).
Слайд 3
Теплопередача - процесс теплообмена между двумя теплоносителями (движущейся

средой, используемой для переноса теплоты) через разделяющую их стенку.
Радиационно-кондуктивный
теплообмен - теплообмен, обусловлен-
совместным переносом теплоты излучением и теплопроводностью.
Радиационио-котективный теплообмен (сложный теплообмен)-телообмен, обусловленный совместным переносом теплоты излуче-нием, теплопроводностью и конвекцией.
Независимо от механизма переноса, тепловой поток всегда направ-лен от более нагретого к менее нагретому телу, а сам процесс теплообмена, согласно второму закону термодинамики, является не-обратимым. Теплообмен между телами зависит от их формы и размеров, а также от времени процесса, так как происходит в конкретных пространственно-временных условиях. Другими важными факторами являются физические свойства тел и их агрегатное состояние. В ре-зультате перепад температур, геометрия и физические свойства тел, агрегатное состояние и параметры теплоносителя, а также время процесса будут определять интенсивность теплообмена и количество переносимой теплоты.
Основным фактором, определяющим интенсивность теплообмена, является температура. Зависимость интенсивности разных видов теп-лообмена от температуры не одинакова, поэтому в различных диапазонах температур" может превалировать тот или иной механизм теп- лопереноса.
Слайд 4
Для количественного описания процесса теплообмена используют следующие величины:
Температура

- в данной точке тела, осредненная по поверхности, осредненная
по объему, осредненная по массе тела. Если соединить точки температурного поля с одинаковой температурой, то получим изотермическую поверхность. При пересечении изотермической поверхности плоскостью получим на этой плоскости семейство изотерм — линий постоянной температуры.
Перепад температур t - разность температур между двумя точками одного тела, двумя изотермическими поверхностями, по-верхностью и окружающей средой, двумя телами. Перепад температуры вдоль изотермы равен нулю. Наибольший перепад температуры происходит по направлению нормали к изотермической поверхности. Возрастание температуры по нормали к изотермической поверхности характеризуется градиентом температуры.
Средний градиент температуры -отношение перепада температур между двумя изотермическими поверхностями к рас-
стоянию между ними, измеренному по нормали n к этим поверх
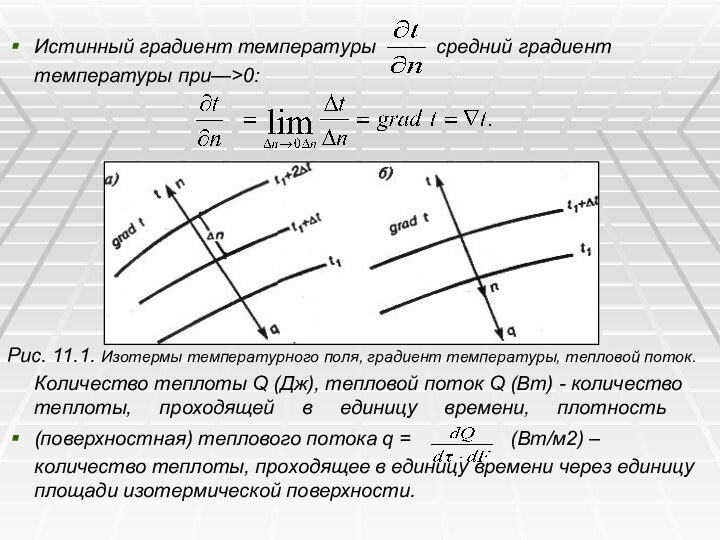
ностям (Рис 11.1)
Слайд 5
Истинный градиент температуры
средний градиент
температуры при—>0:
Рис. 11.1. Изотермы температурного
поля, градиент температуры, тепловой поток.
Количество теплоты Q (Дж), тепловой поток Q (Вт) - количество теплоты, проходящей в единицу времени, плотность
(поверхностная) теплового потока q = (Вт/м2) –
количество теплоты, проходящее в единицу времени через единицу площади изотермической поверхности.
Слайд 6
11.2 ТЕПЛОПРОВОДНОСЬ
Перенос теплоты теплопроводностью (который в чистом виде

имеет место только в твердых телах с малым коэффициентом
термического расширения) выражается эмпирическим законом Био-Фурье, согласно которому вектор плотности теплового потока прямо пропорционален градиенту температуры (1822) q = -XgradT.
Знак «минус» в уравнении (11.2) показывает, что направление теп-лового потока противоположно направлению градиента температуры 'Коэффициент пропорциональности X в уравнении (11.2) характеризует способность тел проводить теплоту и называется коэффициентом теплопроводности. Количественно коэффициент теплопроводности А, -тепловой поток (Вт), проходящий через единицу поверхности (м2) при единичном градиенте температур (К/м), и имеет размерность Вт/(мК).
В технических расчетах значения коэффициента теплопровод-ности обычно берутся по справочным таблицам. Для большого числа мате-риалов эта зависимость оказывается почти линейной, те можно принять 11,3, где Хо - коэффициент теплопроводности при температуре tо; b - по-стоянная, определяемая опытным путем.
Рис. 11.2.
Рассмотрим процесс теплопроводности в однородной плоской стенке толщиной S (рис.11.2). Коэффициент теплопроводности материала стенки л На поверхностях, стенки поддерживаются постоянные температуры tt и t2 (режим стационарный), температурное поле одномерно и меняется только в направлении оси х. Внутренние источники тепла в стенке отсут-ствуют. На основании уравнения для бесконечно тонкого слоя стенки dx, взятого на расстоянии x от поверхности, будем иметь:
q - -X(dlfdx) ИЛИ dt = -(q/)dx и t = -(q /)x + С.
Слайд 8
Постоянная интегрирования С определяется из граничных условий при

х = 0. t – t1, и С –
t1; при x =, t = t2= -(q/)+t1, откуда определяют неизвестную величину плотности теплового потока:
Разность температур (t1 – t2) = называется температурным напором. Отношение , Вт/(м2 К) называется тепловой проводи-мостью стенки, показывающей, какое количество тепла проводит 1м2 стенки за единицу времени при температурном напоре, равном одному градусу Обратная величина тепловой проводимости , К м2/Вт называется термческим соппотивлвнием стенки. Послед-
нее определяет падение температуры при прохождении через стен-ку теплового потока, плотность которого равна единице
Если в выражение t = -q/x + С подставить С = t и q = то получим уравнение температурной кривой:
(11.5)
Уравнение (11.5) показываем что при постоянном значении к внутри однородной плоской стенки температура изменяется по закону прямой линии.
Зная по уравнению (11.5) величину q, просто определить и общее количество тепла Q, переданное через плоскую стенку по-верхностью F в течение времени.
Слайд 9
11.2.1. МНОГОСЛОЙНАЯ ПЛОСКАЯ СТЕНКА.
Рассмотрим плоскую стенку, составленную из несколь-ких, положим
трех, разнородных, плотно прилегающих друг к дру-гу слоев (рис.11.3)
Рис. 11.3. Многослойная плоская стенка
Толщины, и соответствующие коэффициенты теплопроводности составляют , , , и , , .Кроме того, заданы температуры наружных поверхностей стенки и , соприкасающиеся поверхности слоев имеют температуры и , но значения их не известны Поскольку мы рассматриваем стационарный режим, то плотность теплового потока с/, проходящего через каждый слой стенки, по величине одинакова.
Слайд 10
На основании формулы (11.4) для каждого слоя можно
написать:
q= ; q= q=
Решаем уравнения относительно изменения температуры в каждом слое и, складывая их, получаем величину температурного напора
t1-t4= , т.е.
откуда q =
По аналогии для n-слойной стенки расчетную формул можно написать так: q=
Слайд 11
Из полученного уравнения следует, что обшее термическое со-противление
многослойной стенки равно сумме частных термиче-сккх сопротивлений.
Значения неизвестных
температур t2 и t3 определяем как:
t2=t1-q / ; t3=t2-q / =t1-q( / + / ),
или
t3 =t4+q /
Слайд 12
11.2.2. ОДНОСЛОЙНАЯ ЦИЛИНДРИЧЕСКАЯ СТЕНКА. Рассмотрим однородную цилиндрическую
стенку (трубу) длиной l с внутренним диаметром d1 и
наружным d2: Коэффициент теплопроводности материала имеет постоянное значение и равен, На внутренней и наружной поверхности трубы поддерживаются постоянные температуры t1 и t2 (рис11.4), причем t1 > t2. Температурное поле считаем одномерным, т.е. температура метется только в радиальном направлении. В этом случае изотермические поверхности будут представлять собой цилиндрические поверхности, имеющие общую ось с трубой.
Рис.11.4.Однослойная цилиндрическая стена
Слайд 13
Внутри рассматриваемой стенки выделим кольцевой слой с радиусом
r и толщиной dr. По закону Фурье количество тепла
про-ходящего через этот слой за единицу времени, равно:
Разделяя переменные и интегрируя, получим
Используя граничные условия, находим, при r = r1, t=t1 и при r=r2, t=t2.
Тогда
Слайд 14
Вт.тчитая из равенства (б) равенство (в), получим:
или
Решим
последнее равенство относительно Q:
11.7
Для определения закона изменения температуры по толщине цилиндрической стенки подставим в равенство (б) значение С из равенства (в) изначение Q из уравнения (11.7) Получим:
Равенство (11.8) представляет собой уравнение логарифмической кривой
Слайд 15
Плотяость теплового потока для цилиндрической стенки может быть
отнесена к единице внутренней поверхности q1или к единице наружной
поверхности q2. или, чаще всего, к ] пог. м длины трубы q1 В последнем случае
11.9
Соотношение между q1,q2 и q1 получают из равенства:
или
Откуда
Величину q1 называют линейной плотностью теплового потока, ее измеряют единицей Вт/м.