считается неподвижной, а система X'O'Y' движется поступательно по отношению
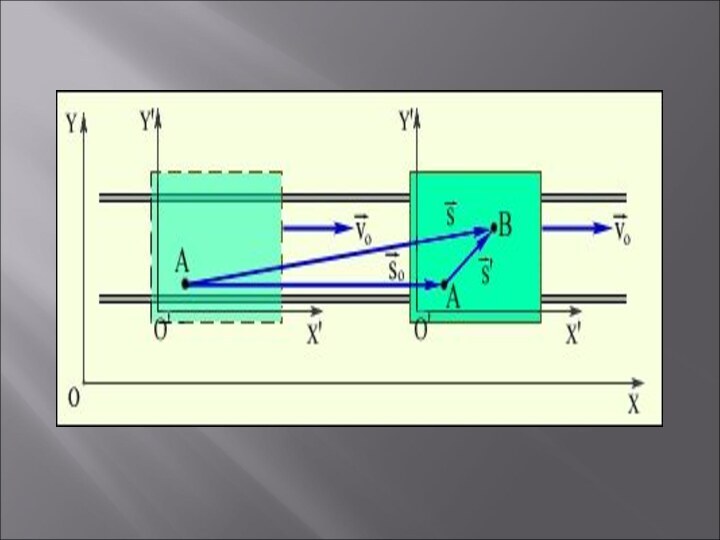
к системе XOY со скоростью Система XOY может быть, например, связана с Землей, а система X'O'Y' – с движущейся по рельсам платформой (рис. 1.2.1).Рисунок 1.2.1. Сложение перемещений относительно разных систем отсчета.
Пусть человек перешел по платформе за некоторое время из точки A в точку B. Тогда его перемещение относительно платформы соответствует вектору а перемещение платформы относительно Земли соответствует вектору Из рис. 1.2.1 видно, что перемещение человека относительно Земли будет соответствовать вектору представляющему собой сумму векторов и
В случае, когда одна из систем отсчета движется относительно другой поступательно (как на рис. 1.2.1) с постоянной скоростью это выражение принимает вид:
Если рассмотреть перемещение за малый промежуток времени Δt, то, разделив обе части этого уравнения на Δt и затем перейдя к пределу при Δt → 0 получим: (*)
Здесь – скорость тела в «неподвижной» системе отсчета XOY, – скорость тела в «движущейся» системе отсчета X'O'Y'. Скорости и иногда условно называют абсолютной и относительной скоростями; скорость называют переносной скоростью.
Соотношение (*) выражает классический закон сложения скоростей: