класса ФМЛ № 38 г.Ульяновска
Руководитель работы:
Алейникова Татьяна
Владимировна - учитель математики
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть






«Элементарные» функции:
Так как функция – это зависимость аргумента и
соответствующего ему значения функции, то будем рассматривать
два направления преобразований – по каждой переменной.
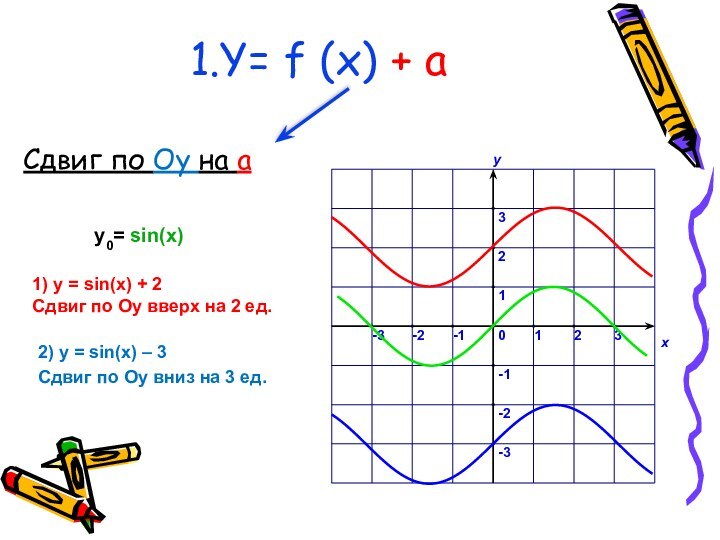
2) у = sin(x) – 3
Сдвиг по Оу вниз на 3 ед.
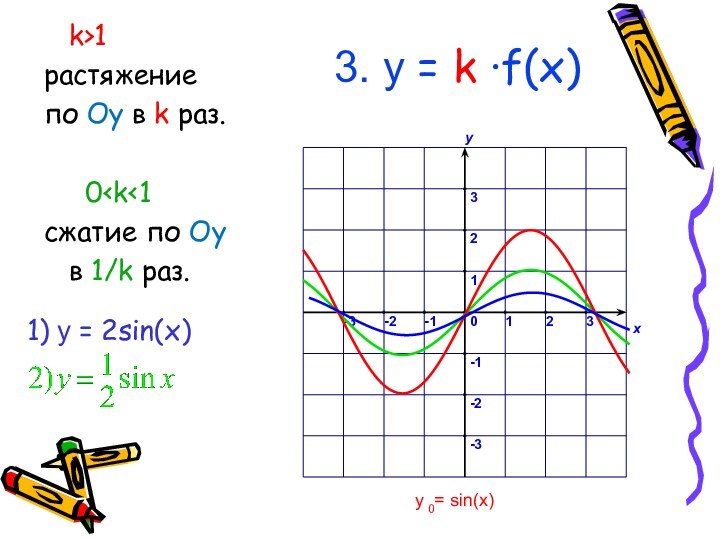
у0= sin(x)
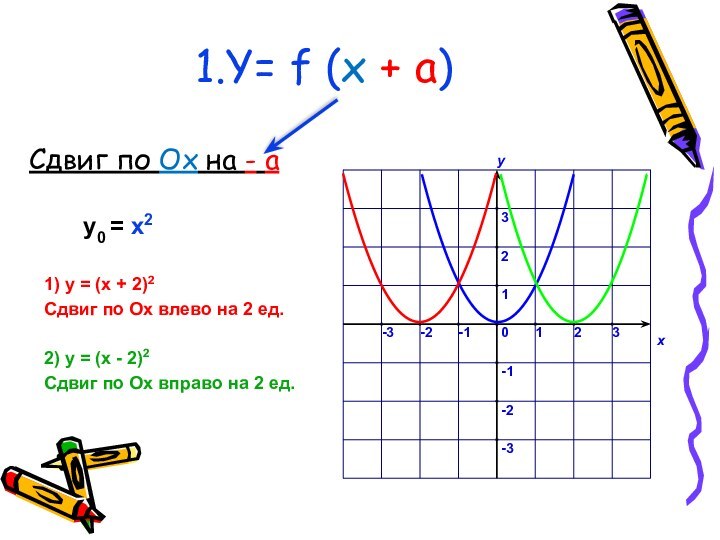
2) у = (x - 2)2
Сдвиг по Ох вправо на 2 ед.
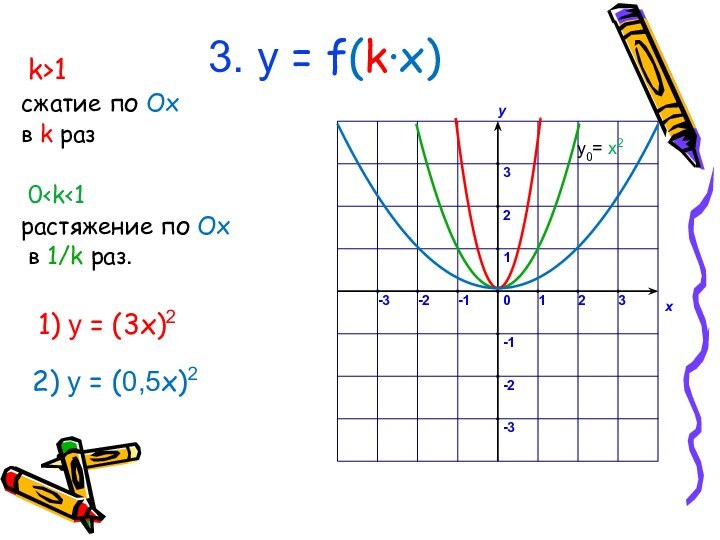
у0 = x2
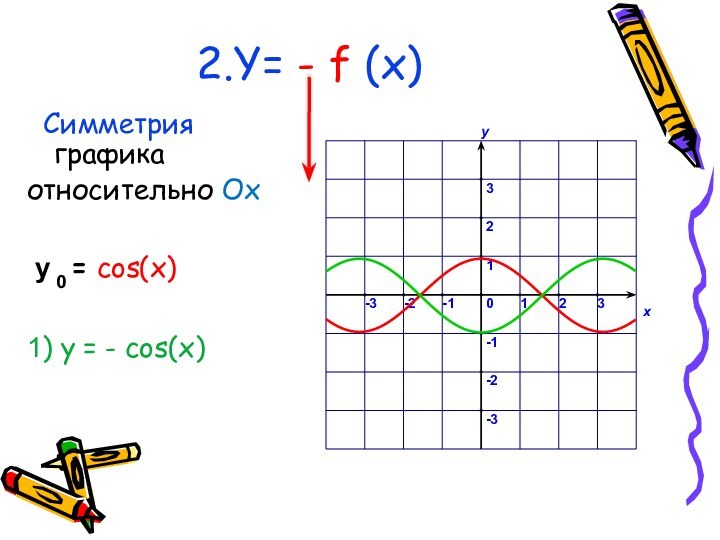
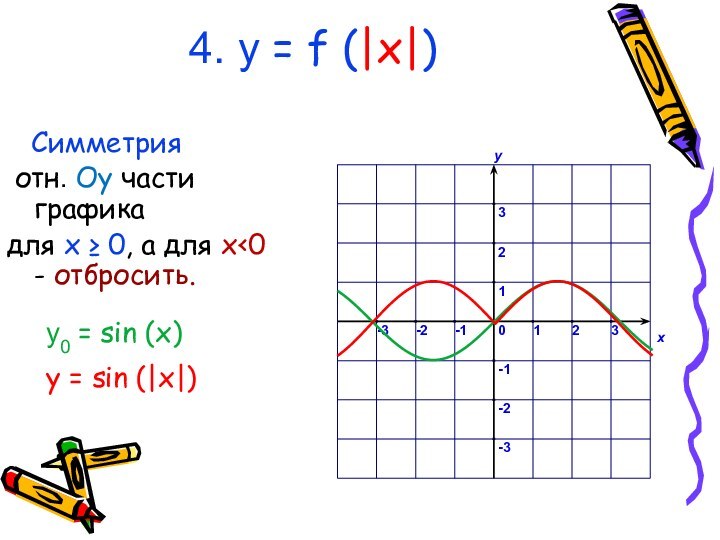
у0 = sin (x)
у = sin (|x|)
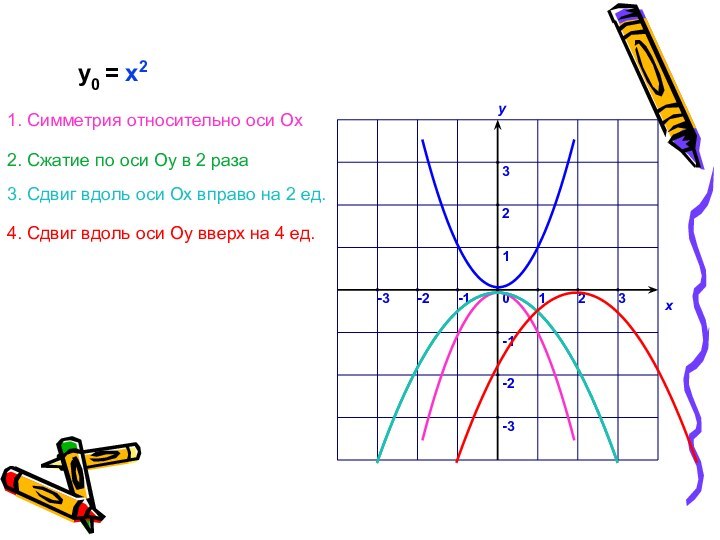
У = - 0,5•(х – 2)2 + 4
Учитывая, что от перестановки мест множителей произведение не
меняется, выполняем преобразования в следующей
последовательности:
1. Симметрия относительно оси Ох (× (-1))
2. Сжатие по оси Оу в 2 раза (× 0,5)
3. Сдвиг вдоль оси Ох вправо на 2 ед.( – 2)
4. Сдвиг вдоль оси Оу вверх на 4 ед.( + 4)
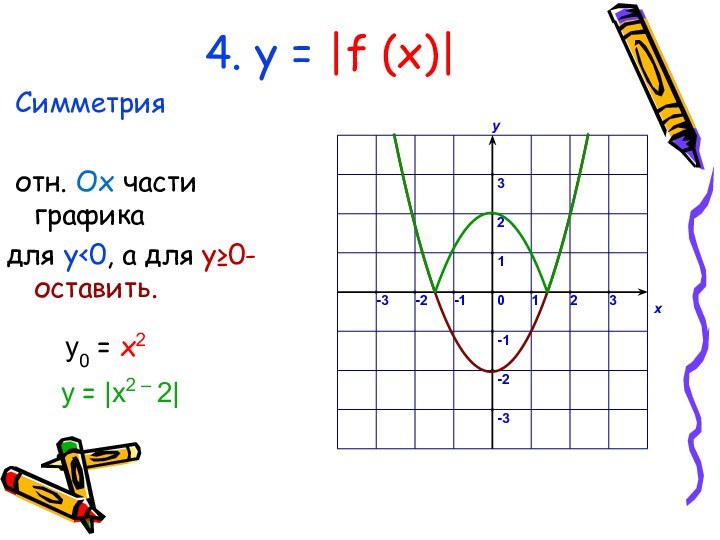
у0 = x2
2 3 1 4
1 2 3 4
или у = -1• 0,5•(х – 2)2 + 4
3. Сдвиг вдоль оси Ох вправо на 2 ед.
4. Сдвиг вдоль оси Оу вверх на 4 ед.