Слайд 2
Содержание
Тема 1 Фаза. Сдвиг фаз.
Тема 2 Получение переменного
тока
Тема 3 Параметры переменного тока
Тема 4 Расчет цепей переменного
тока
4.1 Виды нагрузок переменного тока
4.2 Активное сопротивление (R) в цепи переменного тока
4.3 Цепь с индуктивным сопротивлением (катушкой L)
4.4 Цепь с емкостным сопротивлением (конденсатором С)
4.5 Расчет цепи с резистором и катушкой
4.6 Расчет цепи с резистором и конденсатором
4.7 Расчет цепи с резистором , катушкой и конденсатором
4.8 Расчет разветвленной цепи переменного тока
Тема 5.Резонансные режимы цепи
5.1 Резонанс напряжений
5.2 Резонанс тока
Слайд 3
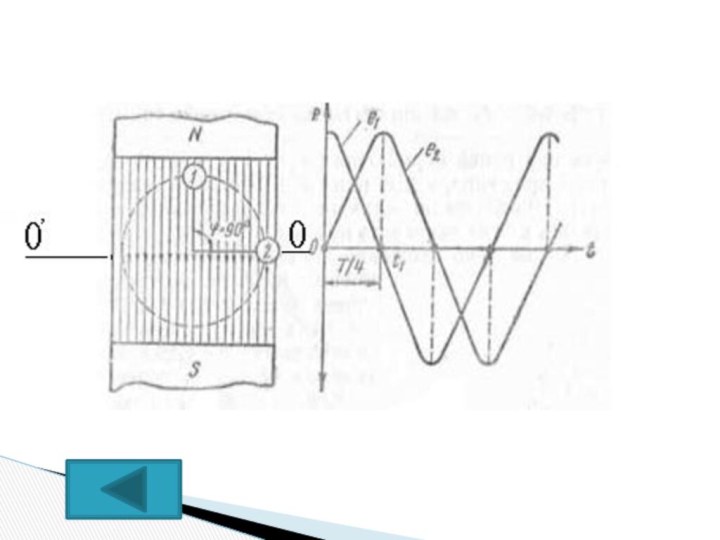
В магнитном поле вращаются два витка. В них
наводится ЭДС одной частоты и амплитуды, но так как
витки находятся под разными углами к нейтральной линии ОО, то
е1=Еm·sin(ω·t)+ψ1
е2=Еm·sin(ω·t)+ψ2
Т. Е. ЭДС своих амплитудных значений достигают не одновременно.
(ω·t+ψ) –фаза
В момент времени t=0 ЭДС отличны от нуля и равны:
е1=Еm·sin ψ1
е2=Еm·sin ψ2
Углы ψ1 и ψ2 характеризуют значения ЭДС в начальный момент времени и называются начальными фазами.
Т.к. начальные фазы ЭДС различны ,то максимальные значения ЭДС достигают не одновременно, а со сдвигом во времени.
ψ1 - ψ2 = φ
Тема 1 Фаза. Сдвиг фаз
Слайд 4
Синусоидальная величина на временной диаграмме характеризуется:
1.Амплитудой
2.Частотой или периодом
3.Начальной
фазой
Переменный ток, напряжение и ЭДС можно представить в виде:
Временной
диаграммы
Уравнения
Вектора
Графически синусоидальные величины изображаются в виде вращающегося вектора Предполагается вращение против часовой стрелки с частотой вращения ω. Длина вектора - действующее ( амплитудное) значение.
Проекция на вертикальную ось есть мгновенное значение
Совокупность двух и более векторов называется векторной диаграммой.
Переменная величина на векторной диаграмме характеризуется:
Действующим значением
Начальной фазой
Слайд 5
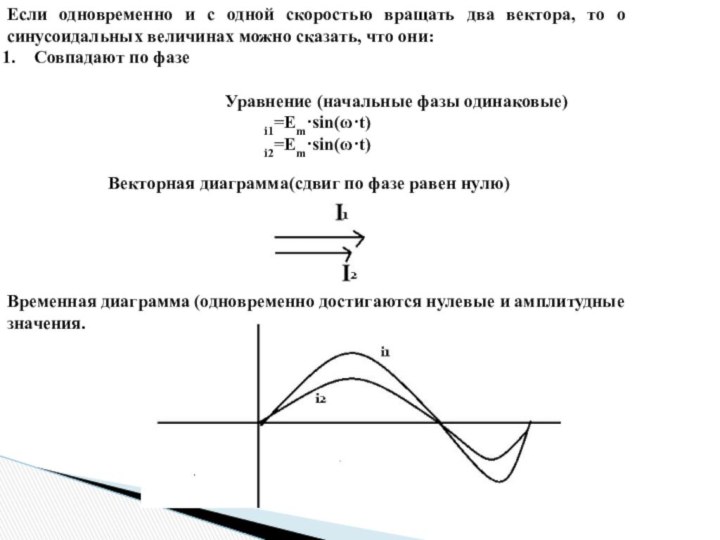
Если одновременно и с одной скоростью вращать два
вектора, то о синусоидальных величинах можно сказать, что они:
Совпадают
по фазе
Уравнение (начальные фазы одинаковые)
i1=Еm·sin(ω·t)
i2=Еm·sin(ω·t)
Векторная диаграмма(сдвиг по фазе равен нулю)
Временная диаграмма (одновременно достигаются нулевые и амплитудные значения.
Слайд 7
2. Сдвинуты по фазе
Временная диаграмма (не одновременно достигаются
нулевые и амплитудные значения). Положительное значение начальных фаз откладывается
влево, отрицательное – вправо.
Векторная диаграмма
Уравнение (начальные фазы не совпадают)
u(t) = Um sin ωt
i(t) = Im sin(ωt -90)
Слайд 8
Тема 2 Получение переменного тока
Ток, периодически меняющийся по
величине и направлению, называется переменным током.
Если кривая изменения тока
описывается синусоидой, то ток называют синусоидальным. Если кривая отличается от синусоиды, то ток несинусоидальный.
Практически в домашних условиях применяют однофазный переменный ток, который получают с помощью генераторов переменного тока. Устройство и принцип действия этих генераторов основывается на явлении электромагнитной индукции — возникновение электрического тока в замкнутом проводнике при изменении магнитного потока, проходящего через него. Это явление было открыто английским ученым М.Фарадеем (1791-1867) в 1831 г.
Простейший генератор – рамка, вращающаяся в магнитном поле постоянного магнита. Концы рамки присоединены к двум медным кольцам 3 и 4, на которых наложены две угольные щетки 5 и 6. Во внешней цепи будет протекать изменяющийся по направлению и величине ток.
Слайд 9
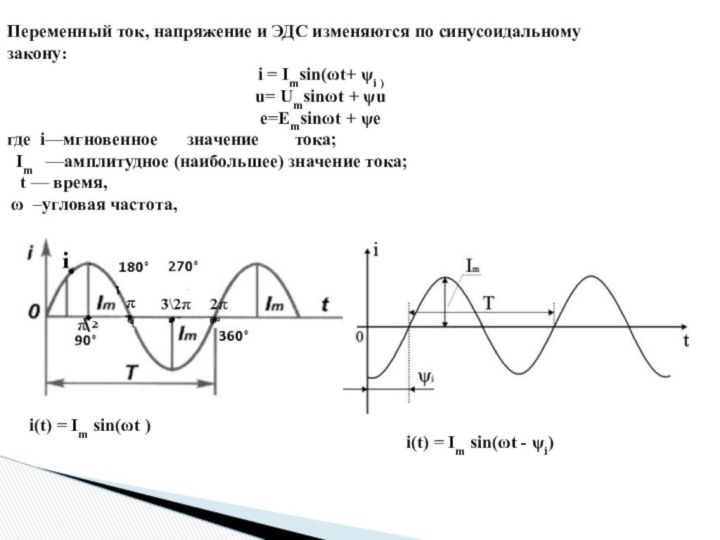
Переменный ток, напряжение и ЭДС изменяются по синусоидальному
закону:
i = Imsin(ωt+ ψi )
u= Umsinωt + ψu
е=Еmsinωt +
ψе
где i—мгновенное значение тока;
Im —амплитудное (наибольшее) значение тока;
t — время,
ω –угловая частота,
i(t) = Im sin(ωt )
i(t) = Im sin(ωt - ψi)
Слайд 10
Тема 3 Параметры переменного тока.
u, i, е -

значение переменного тока, напряжения и ЭДС в любой момент
времени, называемое мгновенным значением переменной величины.
Im Um Еm - Амплитуда - это наибольшее положительное или отрицательное значение переменного тока.
I ,U, Е - действующее значение переменного тока – это такой постоянный ток, который за время одного периода оказывает такое тепловое (механическое и др.) действие, как и данный переменный ток.
I = Im /√2 ≈ 0,707· Im
U = Um / √2 ≈ 0,707· Um
Е = Еm/ √2 ≈ 0,707· Еm
Измерительные приборы, включенные в цепь переменного тока, показывают действующие значения тока или напряжения.
4.Т (сек.) -период - время, в течение которого происходит полное изменение (колебание) тока в проводнике.
5.(f) –частота - число полных колебаний тока за одну секунду. Частота измеряется в герцах (Гц) в честь немецкого ученого Г. Герца (1857-1894). При частоте в 1 Гц происходит одно полное колебание тока за одну секунду. Стандартной частотой переменного тока в России является частота 50 Гц, что соответствует 50 полным колебаниям тока за одну секунду. Частота измеряется с помощью частотомеров.
Слайд 11
Частота - величина, обратная периоду. Следовательно,
f = 1/T или T = 1/f
Частота

переменного тока зависит от частоты вращения ротора генератора и
числа пар полюсов индуктора f =p.n\ 60, Гц
где p—число пар полюсов индуктора;
n—частота вращения ротора в минуту, об\мин.
Если генератор имеет одну пару полюсов, то ротор такого генератора совершает 3000 об/мин для получения переменного тока частотой 50 Гц.
6. ω (рад\сек)– угловая частота или угловая скорость вращения равна углу поворота вектора в единицу времени , ω = α \ t., угол α называется фазным углом или фазой.
Часто вместо градуса применяют радиан – угол, дуга которого равна радиусу.
ω =2·π·f= 2·π\Т , рад\сек.
(град. –начальная фаза или угол.
Задача.
Определить амплитудное значение напряжения в сети, если при сопротивлении цепи 40 Ом амперметр показывает ток 5,5 А.
Из закона Ома напряжение равно U = Ir. Подставив вместо I и r их значения, получим действующее значение напряжения U = 5,5×40 = 220 В.
А так как Um = √2U, то Um= 1,41×220 = 310,2 В.
Слайд 12
Задача.
Найти частоту тока, если период, если период равен
5∙10-8 сек.
f = 1/T = 0,2∙108 Гц или 20 МГц.
Задача.
Определить частоту
переменного тока, получаемого от генератора с 8 полюсами, скорость вращения ротора равна 750 об\мин.
Решение.
f =p.n\ 60= 4 ∙750\60 = 50 Гц.
Задача.
Определить скорость вращения ротора двадцатиполюсного генератора, если частотомер показал частоту тока 25 Гц.
n =60 f\р = 60 ∙25\10 =150 об\мин.
Задача.
ЭДС изменяется по закону: е =8,45 sin 1256 t + Π \4
Определить Е, Т, f, ω, ψ Еm
Решение
Ψ = 90град.= Π \4 рад.
Еm =8,45 В
Е=0,707×8,45=5,97 В
ω=1256 рад\сек
f = ω\2 Π = 1256\6,28 = 200 Гц
T = 1/f = 1\200 =0,005 сек.
Слайд 13
Задача
Действующее значение тока в цепи равно 2,9 А.,
начальная фаза -2\3π, частота 50 Гц. Записать выражения изменения
тока i и определить его амплитуду.
Решение.
i = Imsin(ωt+ ψi )
ω =2·π·f=2 ·з,14·50 =314 рад\сек
Im = 1,41×2,9 = 4 А
i = 4·sin(314·t - 2\3π )
Слайд 14
Тема 4 Расчет цепей переменного тока
4.1 Виды нагрузок

переменного тока
Для цепей переменного тока, в отличие от постоянного,
закон Ома несколько изменяется, так как некоторые виды нагрузок ведут себя при прохождении изменяющегося во времени тока по-разному.
Активная (резистивная) нагрузка. Сопротивление резистора не зависит от частоты. Пример -электрическая лампочка, нагревательный элемент (ТЭН), электрическая плита.
Индуктивная (реактивная) нагрузка преобразует в течение одной половины полупериода энергию электрического тока в магнитное поле, а течении следующей половины преобразует энергию магнитного поля в электрический ток. Пример -дроссель или катушка индуктивности. Сопротивление обозначается XL измеряется в Омах и зависит прямо пропорционально от частоты переменного тока.
Ёмкостная (реактивная) нагрузка преобразует в течение одной половины полупериода энергию электрического тока в электрическое поле, а течении следующей половины преобразует энергию электрического поля в электрический ток. Пример - конденсатор. Сопротивление обозначается XC измеряется в Омах и зависит обратно пропорционально от частоты переменного тока.
Слайд 15
В природе не существует ничего идеального, чистые реактивные
нагрузки в электротехнике не встречаются. Любая нагрузка имеет КПД
ниже 100%, и часть энергии рассеивается в виде тепловых потерь, излучения и т.д. Поэтому в реальной, электротехнике применяется понятие активно-индуктивной нагрузки.
Активно-индуктивная нагрузка может рассматриваться как последовательное или параллельное соединение активного сопротивления и идеальной индуктивности. Пример- трансформатор, электродвигатель, электромагнитное пускорегулирующее устройство для люминесцентных ламп, катушка зажигания в автомобиле. Для этого вида нагрузок характерен бросок напряжения в момент размыкания электрической цепи.
Активно-ёмкостная нагрузка может рассматриваться как последовательное или параллельное соединение активного сопротивления и идеальной ёмкости.
Пример- конденсатор, электронные блоки питания галогенных или люминесцентных ламп.
Слайд 16
Для этих нагрузок характерен бросок тока в момент
замыкания электрической цепи.
При протекании тока через активно-реактивную нагрузку часть
тока будет протекать через прибор, не производя никакой полезной работы. При этом максимумы и минимумы тока и напряжения будут достигаться в разное время, а кривые изменения по времени тока и напряжения будут не совпадать – оставаясь, при этом, периодическими функциями. Происходит сдвиг тока и напряжения по фазе.
Косинус угла между током и напряжением является важной величиной в электротехнике и обозначается cos(φ). Для компенсации cos(φ) и сокращения расходов на электроэнергию применяются конденсаторные установки.
Физический смысл cos(φ) – КПД установки. Этот коэффициент показывает, какая часть тока преобразуется в полезную работу, а какая часть тока течёт в проводниках вхолостую, перегружая проводники. Чем выше cos(φ), тем лучше КПД установки. У активных проводников он равен 1, а у идеальных ёмкостных и индуктивных проводников равен 0.
Слайд 17
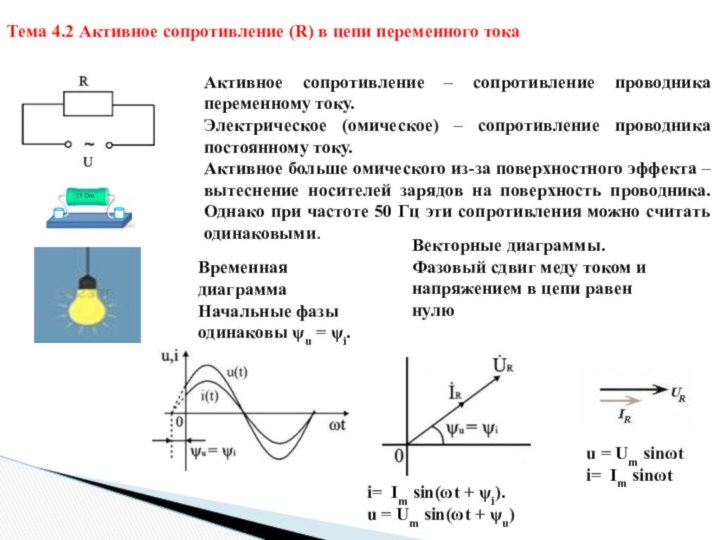
Тема 4.2 Активное сопротивление (R) в цепи переменного
тока
Активное сопротивление – сопротивление проводника переменному току.
Электрическое (омическое) –
сопротивление проводника постоянному току.
Активное больше омического из-за поверхностного эффекта – вытеснение носителей зарядов на поверхность проводника. Однако при частоте 50 Гц эти сопротивления можно считать одинаковыми.
Временная диаграмма Начальные фазы одинаковы ψu = ψi.
Векторные диаграммы. Фазовый сдвиг меду током и напряжением в цепи равен нулю
u = Um sinωt
i= Im sinωt
i= Im sin(ωt + ψi).
u = Um sin(ωt + ψu)
Слайд 18
Цепь обладает только активной мощностью, которая всегда положительная
Р=
I2 R = U I = U2 \ R
Вт
Закон Ома справедлив для мгновенных, максимальных и действующих значений тока I = U \ R
Im = Um \ R
Вывод: В цепи с активным сопротивлением ток и напряжение совпадают по фазе.
Фаза – величина, определяющая взаимоотношение во времени тока и напряжения в электрической цепи.
Задача 1.
В цепь переменного тока с сопротивлением 55 Ом подключили генератор, амплитуда напряжения которого равна 310,2 В. Определить : показания амперметра и вольтметра, мощность цепи.
Решение.
U = Um \ √ 2= 310,2\1,41 =220 В
I = U\ R = 220\55 = 4 А
Р= U I =220∙4 = 880 Вт
Слайд 19
Задача 2.
Решение.
Im=14,1 А
I = Im \ √ 2=
14,1 \1,41 = 10 А
UR1 = I∙R1 = 10∙10
= 100 В
UR2 = I∙R2 = 10∙10 = 100 В
Uобщ. = 100+100 = 200 В
Р= U I = 200∙10 = 2000 Вт
Задача 3.
Дано:
R = 3,6 Ом
Р = 120 Вт
Определить:
I, Im, U, Um
Решение.
Р= I2∙R , поэтому I = √ Р \ R = √120 \ 3,6 = 5,77 А
Im = I∙ √ 2= 5,77∙1,41 = 8,14 А
Um = Im∙ R = 8,14 ∙3,6 = 29 В
U = I∙R = 5,77∙3,6 = 20,77 В
Слайд 20
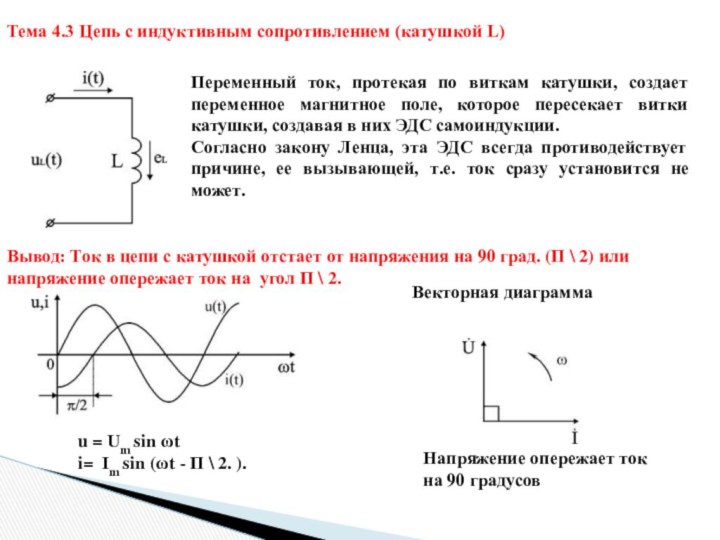
Тема 4.3 Цепь с индуктивным сопротивлением (катушкой L)
Переменный
ток, протекая по виткам катушки, создает переменное магнитное поле,
которое пересекает витки катушки, создавая в них ЭДС самоиндукции.
Согласно закону Ленца, эта ЭДС всегда противодействует причине, ее вызывающей, т.е. ток сразу установится не может.
Вывод: Ток в цепи с катушкой отстает от напряжения на 90 град. (Π \ 2) или напряжение опережает ток на угол Π \ 2.
u = Um sin ωt
i= Im sin (ωt - Π \ 2. ).
Векторная диаграмма
Напряжение опережает ток на 90 градусов
Слайд 21
Мгновенная мощность меняет знак 4 раза.
В первую
четверть периода – положительная, энергия накапливается в магнитном поле
катушки. Катушка – приемник энергии.
Во вторую четверть – отрицательная, энергия обратно возвращается в сеть. Катушка – источник энергии.
Работа не производится. Происходит обмен энергией между катушкой и источником. Расхода энергии не будет, несмотря на то, что в цепи есть ток и напряжение. Активная мощность равна нулю. Провода загружаются реактивной мощностью.
QL = I2 XL = U I ВАр
XL = ωL =2πf L – индуктивное сопротивление катушки.
L – индуктивность катушки, Гн
f – частота , Гц
ω – угловая частота, рад\сек
Закон Ома I = U \ XL Im = Um \ XL
Задача 1 Решение
I = U \ XL отсюда XL= U\ I = 220 \ 0,5 = 440 Ом
XL= 2πf L отсюда L = XL \ 2πf = 440 \ 2∙π∙50 = 1,4 Гн
U = 220 В
I = 0,5 А
F = 50 Гц
Определить :
L - ?
Слайд 22
Задача 2
Дано:
L = 0,01 Гн
f= 300 Гц
U
= 82 В
Определить:
I - ? Написать
закон изменения
тока i и
напряжения u
Решение.
XL= 2πf L = 6,28 ∙300 ∙0,01 = 18,84 Ом
I = U \ XL = 82 \ 18,84 = 4,35 А
Im = I∙ √ 2= 1,41∙4,35 = 6,13 А
ω =2πf = 6,28∙300 = 1884 рад\сек
Um = U∙√2 = 82∙1,41 =115,62 В
u = Um sin ωt = 115,62 sin1884 t
i= Im sin (ωt - Π \ 2. ) = 6,13 sin1884 t - Π\2
Начертить векторную диаграмму тока и напряжения
Слайд 23
Задача 3
Закон изменения напряжения в цепи u =
113,5sin 126 t + Π\2. Индуктивность катушки L =
0,5 Гн. Определить ток в цепи, период, реактивную мощность и закон изменения тока.
Решение.
ω =2πf = 126 рад\сек
f = ω\ 2π =126\6,28 = 20 Гц
Т =1 \ f = 1\20 = 0,05 сек
XL = ωL =126 ∙0,5 = 63 Ома
Im = Um \ XL =113,5\63 = 1,8 А
I = Im \ √ 2= 1,8 \ 1,41 = 1,28 А
QL = I2 XL = 1,282 ∙63 = 103 ВАр
i= 1,8 sin 126 t
Слайд 24
Вопросы по теме
Какой фазовый сдвиг между током и
напряжением в цепи с катушкой?
Какой мощностью обладает данная цепь
и чему она равна?
Чему равна активная мощность цепи?
Напишите закон Ома для цепи с катушкой.
Начертите векторную диаграмму тока и напряжения для цепи с катушкой.
Слайд 25
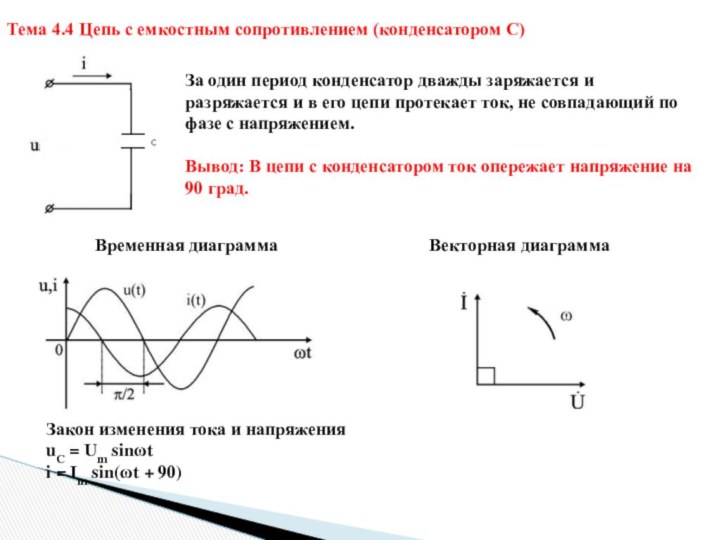
Тема 4.4 Цепь с емкостным сопротивлением (конденсатором С)
За
один период конденсатор дважды заряжается и разряжается и в
его цепи протекает ток, не совпадающий по фазе с напряжением.
Вывод: В цепи с конденсатором ток опережает напряжение на 90 град.
Временная диаграмма
Векторная диаграмма
Закон изменения тока и напряжения
uC = Um sinωt
i = Im sin(ωt + 90)
Слайд 26
Цепь обладает только реактивной мощностью
Qс = I2 Xс = U
I ВАр,
Q берется со знаком (-), т.к. угол
φ< 0
где XC = 1 / (ωC) = 1 \ 2πfC , Ом – емкостное сопротивление конденсатора
ω– угловая частота, об\мин
f– частота, Гц
С - емкость конденсатора, Ф
Закон Ома: I = U \ Xc Im = Um \ Xc
Емкостная нагрузка не потребляет энергию, а в цепи с конденсатором происходит обмен энергией между источником и конденсатором.
Вопрос
С увеличением частоты и емкости уменьшается XC .Почему?
Ответ
Чем больше частота, тем большее количество электричества пройдет через поперечное сечение диэлектрика. Чем больше емкость конденсатора, тем больше электричества переместится по проводам при разрядке или зарядке.
Слайд 27
ЗАДАЧА 1.
В цепь включен конденсатор. Напряжение в цепи
220 В, ток 440 А, частота 50 Гц. Определить
емкость конденсатора.
Решение.
Xc = U \ I = 220\440 = 0,5 Ом
XC = 1 \ 2πfC, отсюда C = 1\ 2πf XC = 1\ 2∙3,14∙ 50∙0,5 = 0,006 Ф
Задача 2
Дано:
С = 2,5 мкФ
u = 24 sin 1884t +15
Определить:
I, i, ВД
Решение.
ω =2πf , отсюда f = ω \ 2π = 1884 \6,28 = 300 Гц
XC = 1 \ 2πf C = 1\ 2∙3,14∙ 300 ∙2,5∙10-6 = 212 Ом
U = Um \ √2= 24\1,41 = 17 В
I = U \ Xc = 17\212 = 0,08 А
Im = I∙ √2 = 1,41∙0,08 = 0,11 А
i = 0,11 sin(1884t + 105)
Слайд 28
Вопросы по теме.
Какой фазовый сдвиг между током и
напряжением в цепи с конденсатором?
Какой мощностью обладает данная цепь
и чему она равна?
Чему равна активная мощность цепи?
Напишите закон Ома для цепи с конденсатором.
Начертите векторную диаграмму тока и напряжения для цепи с конденсатором
Слайд 29
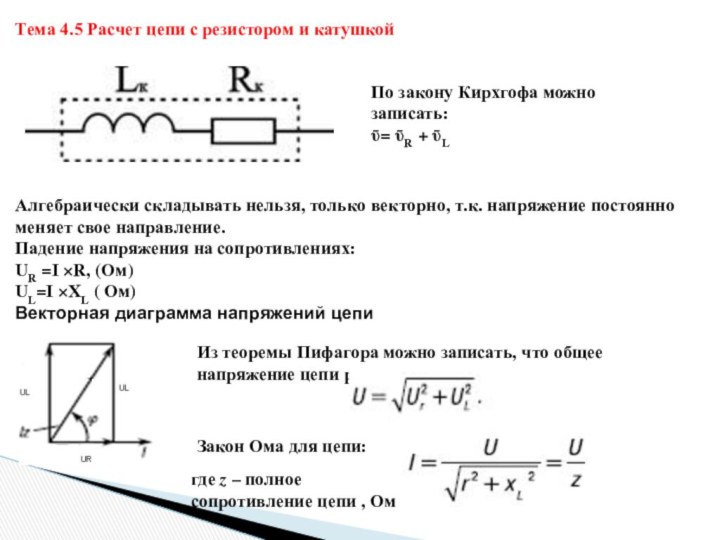
Тема 4.5 Расчет цепи с резистором и катушкой
По
закону Кирхгофа можно записать:
ῡ= ῡR + ῡL
Алгебраически складывать нельзя,
только векторно, т.к. напряжение постоянно меняет свое направление.
Падение напряжения на сопротивлениях:
UR =I ×R, (Ом)
UL=I ×XL ( Ом)
Векторная диаграмма напряжений цепи
Из теоремы Пифагора можно записать, что общее напряжение цепи равно
Закон Ома для цепи:
где z – полное сопротивление цепи , Ом
Слайд 30
ВЫВОД: в такой цепи напряжение опережает ток на
угол φ (положительный).
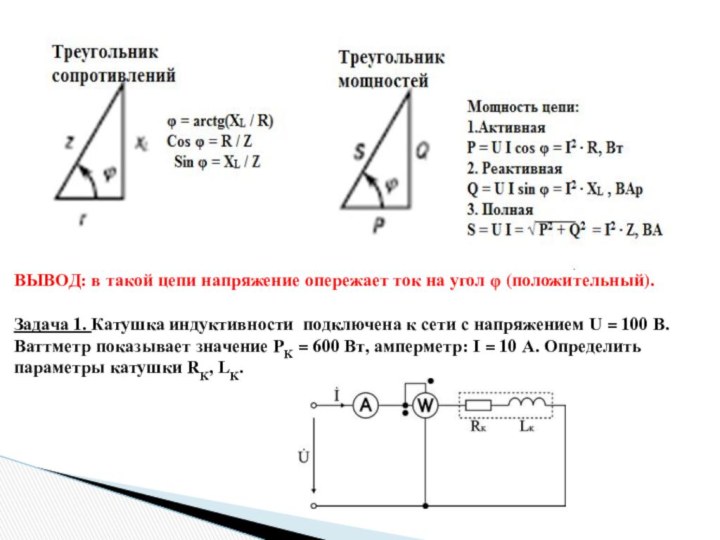
Задача 1. Катушка индуктивности подключена к сети с
напряжением U = 100 В. Ваттметр показывает значение PK = 600 Вт, амперметр: I = 10 А. Определить параметры катушки RK, LK.
Слайд 31
1. Вычисление полного сопротивления катушки
ZК = U /
I = 100 / 10 = 10 Ом.
2. Вычисление
активного сопротивления катушки RК
Ваттметр измеряет активную мощность, которая в данной схеме потребляется активным сопротивлением RК.
RК = PК / I2 = 600 / 100 = 6 Ом.
3. Вычисление индуктивности катушки LК
XК = 2πf LК; LК = XК / (2πf) = 8 / (2π×50) = 0,025 Гн.
Дополнительные вопросы к задаче
1. Как решить задачу другим способом?
Параметры катушки индуктивности можно определить, рассчитав полную мощность SК и реактивную мощность катушки QК.
SК = U I = 100 · 10 = 1000 ВА.
RК = PК / I2 = 6 Ом; XК = QК / I2 = 8 Ом;
Слайд 32
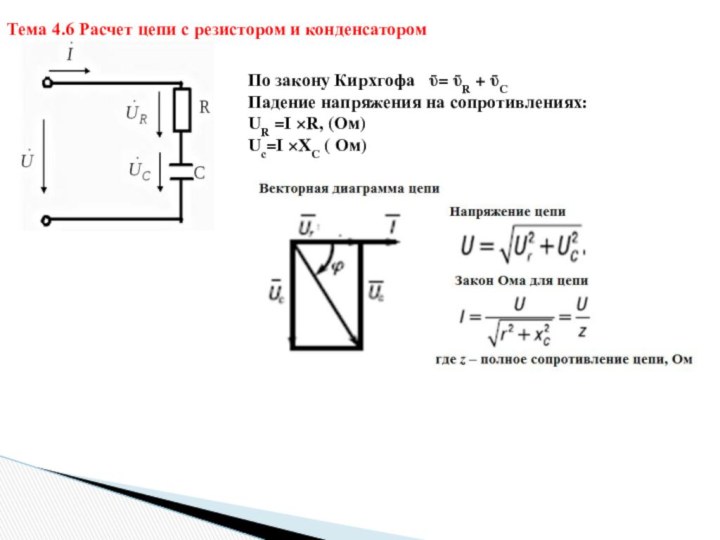
Тема 4.6 Расчет цепи с резистором и конденсатором
По
закону Кирхгофа ῡ= ῡR + ῡC
Падение напряжения на
сопротивлениях:
UR =I ×R, (Ом)
Uс=I ×XC ( Ом)
Слайд 33
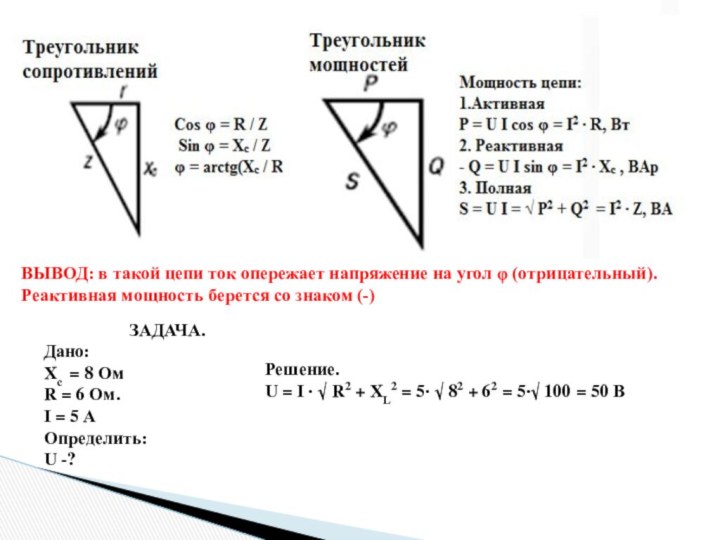
ВЫВОД: в такой цепи ток опережает напряжение на
угол φ (отрицательный).
Реактивная мощность берется со знаком (-)
ЗАДАЧА.
Дано:
Xс =
8 Ом
R = 6 Ом.
I = 5 А
Определить:
U -?
Решение.
U = I ∙ √ R2 + XL2 = 5∙ √ 82 + 62 = 5∙√ 100 = 50 В
Слайд 34
Тема 4.7 Расчет цепи с резистором , катушкой
и конденсатором
Для напряжений выполняется второй закон Кирхгофа в векторной
форме.
Ú = ÚR + ÚL + ÚC.
Напряжения на элементах определяются по формулам
UR = I R, ψuR = ψi ;
UL = I XL, ψuL = ψi + 90° ;
UC = I XC, ψuC = ψi - 90°.
В зависимости от величин L и С в формуле , возможны следующие варианты:
1. XL > XC;
2. XL < XC;
Слайд 35
1 вариант: XL > XC , тогда UL > UC.
Строим векторную
диаграмму
Вывод: Так как ток отстает от напряжения на угол φ
(угол φ > 0), то цепь имеет индуктивный характер
Самостоятельно нарисовать треугольник сопротивлений и мощности в цепи.
Слайд 36
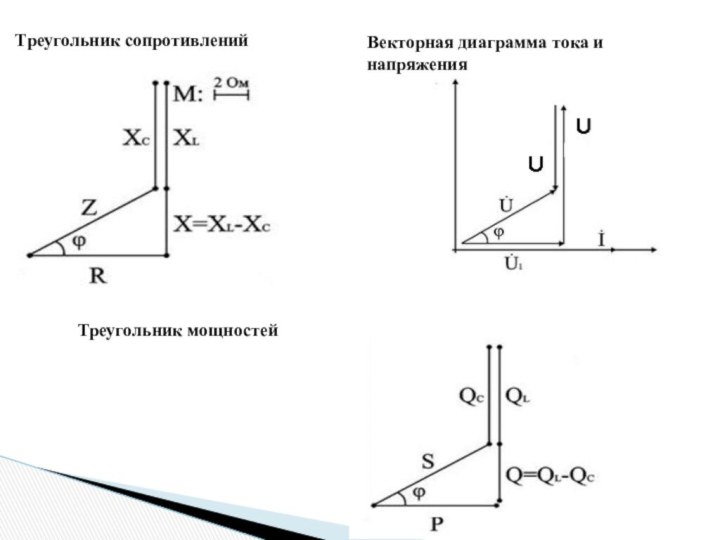
Треугольник сопротивлений
Векторная диаграмма тока и напряжения
Треугольник мощностей
Слайд 38
Вывод: Так как ток опережает напряжение на угол
φ (угол φ
Самостоятельно нарисовать треугольник сопротивлений и мощности в цепи.
Задача
Электрическая цепь, показанная на рис. питается от источника синусоидального тока с частотой 200 Гц и напряжением 120 В. Дано: R = 4 Ом, L = 6,37 мГн, C = 159 мкФ.
Вычислить ток в цепи, напряжения на всех участках, активную, реактивную, и полную мощности. Построить векторную диаграмму, треугольники сопротивлений и мощностей.
Слайд 39
Решение
Вычисление сопротивлений участков и всей цепи
Индуктивное реактивное сопротивление
XL
= 2πf L = 2×3,14×200×6,37·10-3 = 8 Ом.
Емкостное реактивное
сопротивление
XC = 1 / (2πf C) = 1 / (2×3,14×200×159·10-6) = 5 Ом.
Полное сопротивления всей цепи:
X = XL - XC = 8-5 = 3 Ом;
2. Вычисление тока и напряжений на участках цепи
Ток в цепи
I = U / Z = 120 / 5 = 24 А.
Напряжения на участках:
UR = R I = 96 В; UL = XL I = 192 В; UC = XC I = 120 В.
3. Вычисление мощностей
Активная мощность
P = R I2 = UR I = 2304 Вт.
Реактивные мощности:
QL = XL I2 = UL I = 4608 вар; QC = XC I2 = UC I = 2880 вар.
Полная мощность цепи
Слайд 40
4. Угол сдвига фаз
В данной цепи ток отстает
по фазе от напряжения на угол 37 град.
Слайд 41
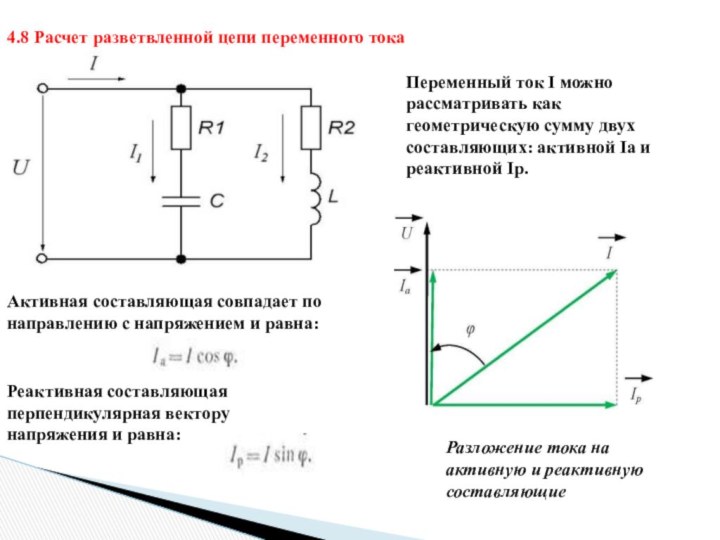
4.8 Расчет разветвленной цепи переменного тока
Переменный ток I
можно рассматривать как геометрическую сумму двух составляющих: активной Iа
и реактивной Iр.
Разложение тока на активную и реактивную составляющие
Активная составляющая совпадает по направлению с напряжением и равна:
Реактивная составляющая перпендикулярная вектору напряжения и равна:
Слайд 42
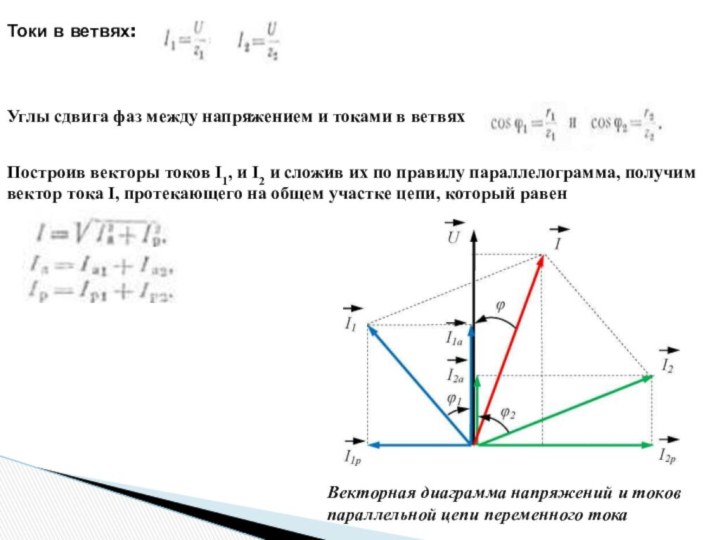
Токи в ветвях:
Углы сдвига фаз между напряжением и
токами в ветвях
Построив векторы токов I1, и I2 и
сложив их по правилу параллелограмма, получим вектор тока I, протекающего на общем участке цепи, который равен
Векторная диаграмма напряжений и токов параллельной цепи переменного тока
Слайд 43
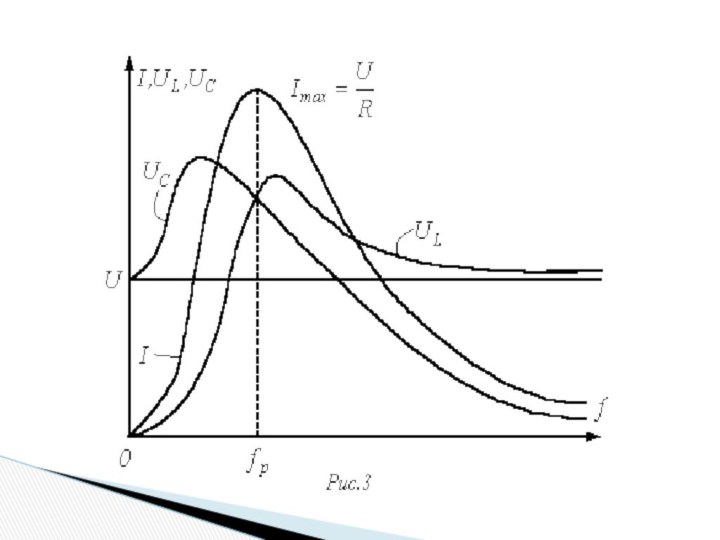
Тема 5.Резонансные режимы цепи
5.1 Резонанс напряжений
Режим работы неразветвленной
электрической цепи , когда ток и напряжение совпадают по
фазе, а сопротивление цепи является чисто активным.
Физическая сущность резонанса заключается в периодическом обмене энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, причем сумма энергий полей остается постоянной.
Условия резонанса:
Цепь неразветвленная
XL = XC
Свойства цепи при резонансе
Т.к. реактивные сопротивления равны, падения напряжения на индуктивности и емкости равны и много больше напряжения цепи. UL = UC >>U
Падение напряжения на активном сопротивлении совпадает по фазе с напряжением цепи UR = U
Слайд 44
3.Ток в цепи максимальный и равен
Полное сопротивление
минимальное и равно Z = R
Реактивная мощность равна нулю.
Коэффициент мощности равен единице:
cos φ = P/S = R/Z= 1.
Явление резонанса находит применение в радиотехнике для получения максимального тока и напряжения в контуре.(антенный контур радиопередатчика настраивают на резонанс напряжений для того, чтобы ток в антенне был максимальным. Тогда дальность действия передатчика будет наибольшей). Однако, если он возникает стихийно, то может привести к аварийным режимам вследствие появления больших перенапряжений и сверхтоков.
Резонансная частота
Слайд 46
5.2 Резонанс тока
Режим работы разветвленной электрической цепи ,
когда ток и напряжение в неразветвленной части цепи совпадают
по фазе.
Условия резонанса:
Цепь разветвленная
XL = XC
Свойства цепи при резонансе
Общий ток может быть значительно меньше токов в каждой ветви.
Ток и напряжение совпадают по фазе.
3.При резонансе токов коэффициент мощности равен единице: cos φ = 1.
4. Полная мощность равна активной мощности: S = P.
5. Реактивная мощность равна нулю: Q = QL - QC = 0.
Слайд 47
Задача 1
Дано:
U = 220 B,
f = 50 Гц,
R = 22 Ом,
L = 350 мГн,
С = 28,9 мкФ.
Найти:
I, UL, UC , φ-?
Индуктивное сопротивление
XL = ωL = 2πf L = 2 · 3,14 · 50 · 0,35 = 110 Ом;
Емкостное сопротивление
XC = 1 / ωC = 1 / (2πf C) = 110 Ом;
Полное сопротивление
Z = R = 22 Ом,
Угол сдвига между током и напряжением
φ=0
Слайд 48
Ток в цепи
I = U / R = 220
/ 22 = 10 А
Напряжение на индуктивности и емкости
UL
= UC = I XL = 10 · 110 = 1100 В.
Задача 2
Определить частоту сети, при которой в цепи возникает резонанс напряжений. Определить также, во сколько раз напряжение на индуктивности больше напряжения сети при резонансе, если цепь имеет следующие параметры:
r = 20 Ом, L = 0,1 Гн, С = 5 мкф.
Решение.
Резонансная частота
Индуктивное сопротивление цепи при резонансе
xL = 2π f0 L = 6,28 • 224 • 0,l = 140 Ом.
Напряжение на индуктивности при резонансе
UL / U = IxL/ Ir, UL = U xL / r = U 140 /20= 7U.
Напряжение на индуктивности при резонансе в 7 раз больше напряжения сети.
Слайд 49
Контрольные вопросы
1.Что такое резонанс напряжений, чем он характеризуется?
2.Что
такое резонанс токов, чем он характеризуется?
3.В чем физическая сущность
резонансных режимов?