Презентация на тему Расхождение вектора скорости. Циркуляция вектора скорости. Ламинарное движение вдоль пластины

Содержание

2. На рисунке приведены изотахи для расходных составляющих
3. Скалярное произведение оператора Δ на вектор ā есть величина скалярная и называется дивергенцией или расхождением вектора.
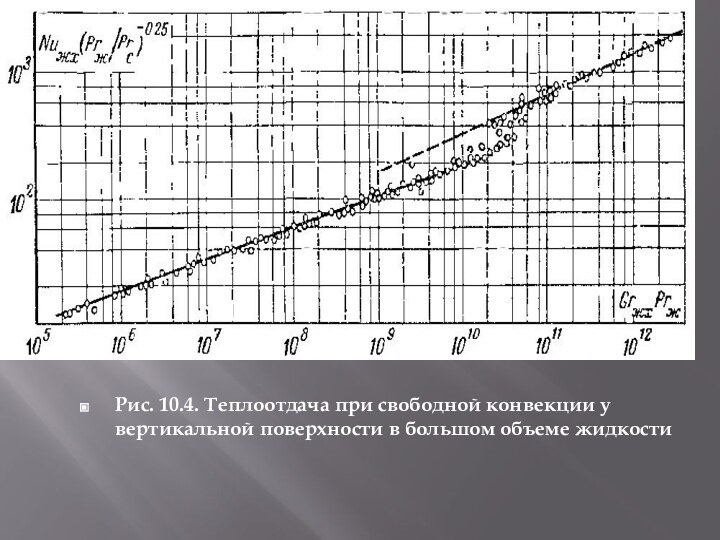
4. Теплоотдача при свободном ламинарном движении вдоль вертикальной
5. Будем полагать, что температура в движущемся слое
6. Из уравнения (10.1) следует, что
7. Уравнение распределения скоростей в движущемся слое жидкости:На
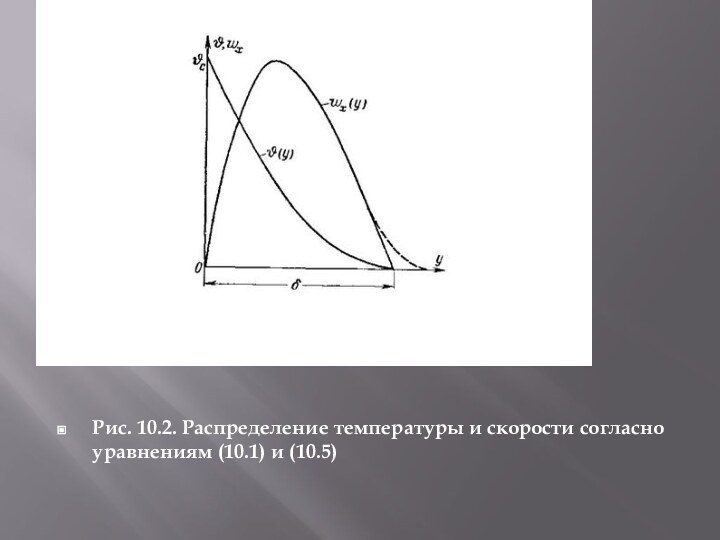
8. Рис. 10.2. Распределение температуры и скорости согласно уравнениям (10.1) и (10.5)
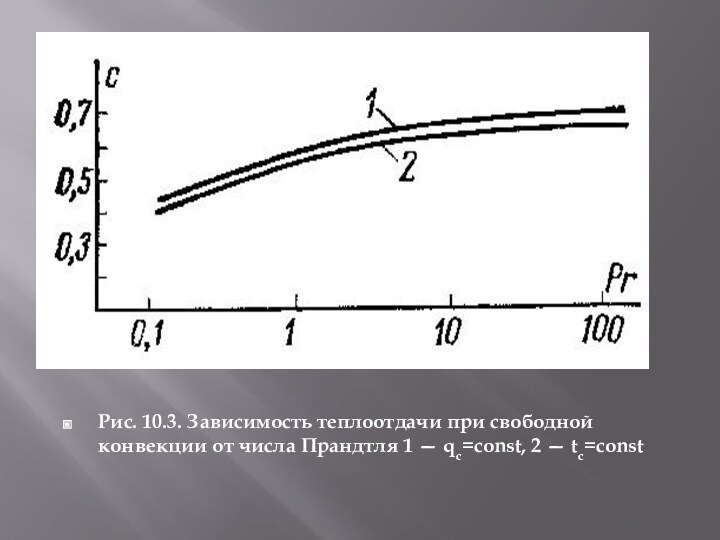
9. Рис. 10.3. Зависимость теплоотдачи при свободной конвекции от числа Прандтля 1 — qc=const, 2 — tc=const
10. Скачать презентацию
11. Похожие презентации

На рисунке приведены изотахи для расходных составляющих скоростей в выходном сечении патрубка турбины.В непрерывном поле скалярной величины через любую точку пространства можно провести линию постоянного значения этой скалярной величины. При этом в каждой точке скалярного поля

Главная
Физика
Расхождение вектора скорости. Циркуляция вектора скорости. Ламинарное движение вдоль пластины

Расхождение вектора скорости. Циркуляция вектора скорости. Ламинарное движение вдоль пластины.

На рисунке приведены изотахи для расходных составляющих скоростей в выходном сечении патрубка

Скалярное произведение оператора Δ на вектор ā есть величина скалярная и называется дивергенцией или расхождением вектора.

Теплоотдача при свободном ламинарном движении вдоль вертикальной пластины.Для упрощения решения задачи примем

Будем полагать, что температура в движущемся слое жидкости изменяется по уравнениюсогласно условию

Уравнение распределения скоростей в движущемся слое жидкости:На рис. 10.2 приведено распределение скоростей

Рис. 10.2. Распределение температуры и скорости согласно уравнениям (10.1) и (10.5)

Рис. 10.3. Зависимость теплоотдачи при свободной конвекции от числа Прандтля 1 — qc=const, 2 — tc=const

Рис. 10.4. Теплоотдача при свободной конвекции у вертикальной поверхности в большом объеме жидкости

Слайды презентации

Слайд 2 На рисунке приведены изотахи для расходных составляющих скоростей

На рисунке приведены изотахи для расходных составляющих скоростей в выходном сечении

в выходном сечении патрубка турбины.
В непрерывном поле скалярной величины

через любую точку пространства можно провести линию постоянного значения этой скалярной величины. При этом в каждой точке скалярного поля значение производной от рассматриваемой величины будет зависеть от выбора направления. По направлениям касательных к линиям постоянного значения производные равны нулю, а по нормали к этой линии производные будут иметь наибольшие значения. Градиент скалярной функции есть вектор, направленный по нормали к линии постоянного значения скалярной функции в сторону увеличения этой функции и равный по величине производной по направлению указанной нормали.

Слайд 3 Скалярное произведение оператора Δ на вектор ā есть

величина скалярная и называется дивергенцией или расхождением вектора.

Слайд 4 Теплоотдача при свободном ламинарном движении вдоль вертикальной пластины.
Для

Теплоотдача при свободном ламинарном движении вдоль вертикальной пластины.Для упрощения решения задачи

упрощения решения задачи примем следующие допущения:
силы инерции пренебрежимо малы

по сравнению с силами тяжести и вязкости;
конвективный перенос теплоты, а также теплопроводность вдоль движущегося слоя жидкости можно не учитывать;
градиент давления равен нулю;
физические параметры жидкости (исключая плотность) постоянны; плотность является линейной функцией температуры.