Слайд 2
1.1. Введение
Оптика – (от
греч. optike – наука о зрительных восприятиях) – раздел
физики, в котором изучаются оптическое излучение (свет), его распространение и явления, наблюдаемые при взаимодействии света и вещества.
Оптическое излучение представляет собой электромагнитные волны, и поэтому оптика – часть общего учения об электромагнитном поле.
Огромная часть информации об окружающем нас мире поступает в виде электромагнитного излучения. Свет, с помощью которого мы видим, составляет только небольшую часть спектра электромагнитных волн рис. 1.1,а).
Слайд 3
Рис. 1.1.а. Шкала электромагнитных излучений. По горизонтальной оси
отложены: внизу –длина волны, м; вверху – частота колебаний,
Гц
Слайд 4
Разные части спектра характеризуются разными значениями «длины волны».
По мере того как длина волны пробегает значения в
пределах спектра видимого света, цвет световых лучей меняется от λ = 760 нм (красный свет) до λ = 390 нм (фиолетовый свет). Это видимый диапазон (рис. 1.1,б).
Рис. 1.1,б
Видимый свет
Слайд 5
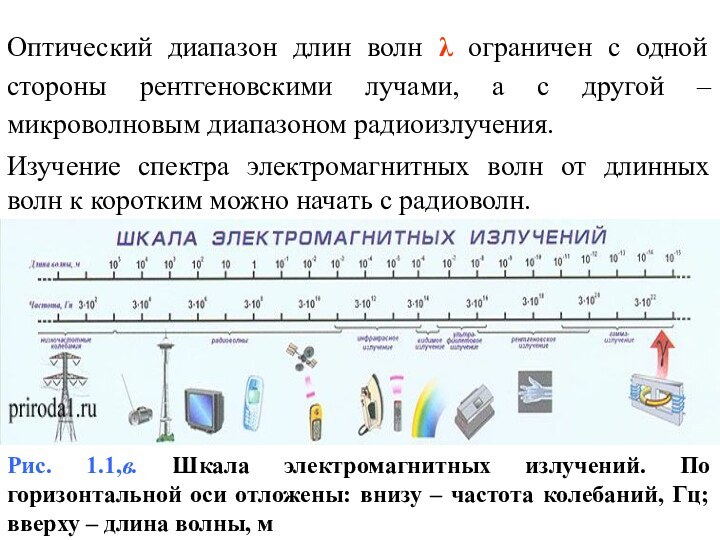
Оптический диапазон длин волн ограничен с одной
стороны рентгеновскими лучами, а с другой – микроволновым диапазоном
радиоизлучения.
Изучение спектра электромагнитных волн от длинных волн к коротким можно начать с радиоволн.
Рис. 1.1,в. Шкала электромагнитных излучений. По горизонтальной оси отложены: внизу – частота колебаний, Гц; вверху – длина волны, м
Слайд 6
Длины электромагнитных волн радиодиапазона заключены в пределах от
10 км до 0,001 м (1 мм). Диапазон от 1 мм до видимого
излучения (т.е. 760 нм) называется инфракрасным диапазоном. Электромагнитные волны с длиной волны короче 390 нм называются ультрафиолетовыми волнами. Наконец, в самой коротковолновой части спектра лежит излучение рентгеновского и гамма-диапазона.
Слайд 7
Всякое излучение можно рассматривать как поток квантов –
фотонов, распространяющихся со скоростью света, равной с = 299 792 458 м/с. Скорость света
связана с длиной и частотой волны соотношением
с = λ∙ν.
Энергию квантов света E можно найти, зная его частоту:
E = h∙ν,
где h – постоянная Планка, равная h ≈ 6,62610–34 Джс. Энергия квантов измеряется в джоулях или электрон-вольтах: 1 эВ = 1,6 10–19 Дж. Кванту с энергией в 1 эВ соответствует длина волны λ = 1240 нм.
Слайд 8
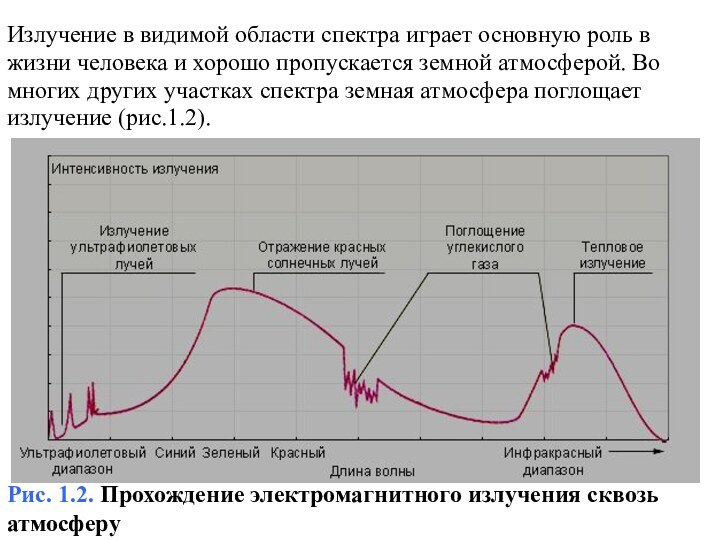
Излучение в видимой области спектра играет основную роль
в
жизни человека и хорошо пропускается земной атмосферой. Во
многих других
участках спектра земная атмосфера поглощает
излучение (рис.1.2).
Рис. 1.2. Прохождение электромагнитного излучения сквозь атмосферу
Слайд 9
Видимая область спектра регистрируется оптическими телескопами, а также
невооруженным глазом. Глаз – это естественный измерительный прибор, регистрирующий
электромагнитное излучение в видимой области спектра.
Площадь зрачка может изменяться в 100 раз, тем самым регулируя поток света, поступающего на сетчатку в дневное время. Днем освещенность от Солнца составляет 105 лк, в то время как ночью звездное небо создает освещенность всего в 10–5 лк. Поэтому для того, чтобы видеть в темноте, регистрировать излучение должны не колбочки, а палочки – другие элементы глаза.
Слайд 10
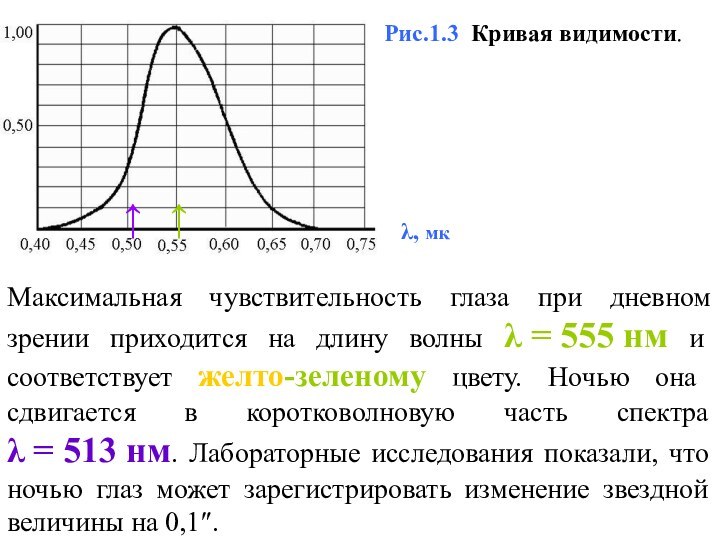
Рис.1.3 Кривая видимости.
λ, мк
Максимальная чувствительность глаза при дневном
зрении приходится на длину волны λ = 555 нм и соответствует желто-зеленому
цвету. Ночью она сдвигается в коротковолновую часть спектра λ = 513 нм. Лабораторные исследования показали, что ночью глаз может зарегистрировать изменение звездной величины на 0,1.
Слайд 11
Между разными диапазонами нет никаких границ. Числа, которые
соответствуют разным диапазонам, и сами названия диапазонов весьма условны
и в значительной степени определяется общностью технических средств и методов исследования явлений в указанном диапазоне.
В пределах обширного диапазона длин волн имеется не менее трех областей, где возможны весьма интересные приближения.
I область длина волны мала по сравнению с размерами приборов, с помощью которых изучают такие волны; более того, энергия фотонов, если говорить на языке квантовой механики, меньше порога чувствительности приборов. В этой области первое приближение дает метод геометрической оптики.
Слайд 12
II область – когда длина волны становится порядка
размеров прибора (такие условия проще создать для радиоволн, чем
для видимого света), а энергия фотонов по-прежнему ничтожна.
В этом случае применяется другое очень полезное приближение, в котором учтены волновые свойства света, но пренебрегается эффектами квантовой механики.
Это приближение основано на классической теории электромагнитного излучения волновой оптике.
Слайд 13
III область – еще более коротких длин волн,
когда энергия фотонов велика по сравнению с чувствительностью приборов
и от волнового характера излучения можно отвлечься – корпускулярное поведение света, как совокупности некоторых частиц – фотонов – квантовая оптика.
По традиции оптику принято подразделять на геометрическую, физическую и физиологическую.
Слайд 14
Геометрическая оптика, не рассматривая
вопрос о природе света, исходит
из эмпирических
законов его распространения и использует
представление о световых лучах,
отражающихся и
преломляющихся на границах сред с разными
оптическими свойствами и прямолинейных в
оптически однородной среде.
Наибольшее значение геометрическая оптика имеет для расчета и конструирования оптических приборов – от очковых линз до сложных объективов и огромных астрономических инструментов.
Слайд 15
Физическая оптика рассматривает проблемы, связанные с процессами испускания
света, природой света и световых явлений.
В физической оптике
сформировалось новое направление, связанное с генерированием вынужденного излучения и созданием квантовых усилителей и квантовых генераторов излучения (мазеров и лазеров).
Излучение лазеров обладает большой временной и пространственной когерентностью, высокой монохроматичностью, предельно малой расходимостью пучка и при фокусировке позволяет получать недостижимые ни для каких других источников напряженности электрического поля, превышающие внутриатомные.
Слайд 17
Начнем с геометрической оптики, где длина волны и
фотонный характер света роли не играют. Геометрическая оптика, хотя
и является приближением, представляет огромный интерес с технической и исторической точек зрения.
Со светом человек знаком с момента рождения. Возникает первая проблема: каков механизм видения света? Теорий было много, но, в конце концов, они свелись к одной: существует нечто, попадающее в глаз при отражении от предметов. Эта идея существует уже давно и столь привычна, что теперь даже трудно себе представить другие идеи, предложенные, однако, весьма умными людьми, например, что нечто выходит из глаза и чувствует окружающие предметы.
Были и другие важные наблюдения: свет распространяется из одной точки в другую по прямой линии, если ничто ему не препятствует и лучи света не взаимодействуют друг с другом.
Слайд 18
При конструировании многих оптических приборов приближение геометрической оптики
оказывается особенно полезным. Геометрическая оптика и очень проста, и
очень сложна. Уже поверхностное изучение геометрической оптики позволяет с помощью простых правил составлять схемы приборов. Но если при этом учитывать искажения в линзах, то задача становится слишком сложной.
Законы и уравнения геометрической оптики могут быть получены теоретически из волнового уравнения (или уравнений Максвелла для электромагнитного излучения) предельным переходом к исчезающе малой длине волны
λ → 0.
Слайд 19
1.2. Законы геометрической оптики
Еще до установления природы света
были известны следующие основные законы оптики: закон прямолинейного распространения
света в оптически однородной среде; закон независимости световых пучков (справедлив только в линейной оптике); закон отражения света; закон преломления света.
1.2.1. Прямолинейное распространение света
Закон прямолинейного распространения света:
свет в оптически однородной среде
распространяется прямолинейно.
Прямолинейность световых лучей означает, что форма тени предмета при его освещении точечным источником соответствует геометрической центральной проекции контура предмета (с центром в источнике) (рис. 1.4). Этот закон имеет
Слайд 20
При освещении предмета протяженным источником света края тени
оказываются размытыми. В переходную область между полной тенью и
светом (в область полутени) попадают лучи не от всех точек источника (рис. 1.5).
Рис. 1.4. Тень, отбрасываемая предметом, обусловлена прямолинейностью распространения световых лучей в оптически однородных средах
глубокий смысл, ибо само понятие прямой линии сформировалось главным образом на основе оптических наблюдений. Закон этот встречается в сочинении по оптике Евклида (300 лет до н.э.).
Слайд 21
Рис. 1.5. Образование тени и полутени для протяженных
источников света
Астрономической иллюстрацией прямолинейного распространения света и, в частности,
образования тени и полутени может служить затенение одних планет другими, например затмение Луны, когда Луна попадает в тень Земли.
Слайд 22
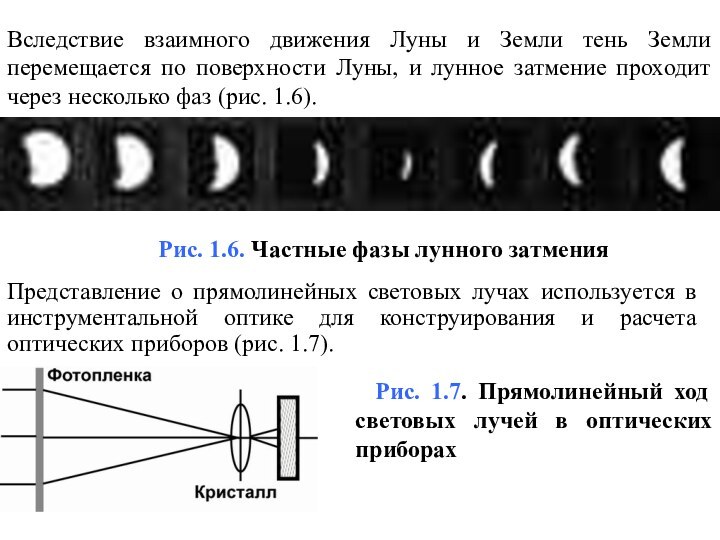
Вследствие взаимного движения Луны и Земли тень Земли
перемещается по поверхности Луны, и лунное затмение проходит через
несколько фаз (рис. 1.6).
Рис. 1.6. Частные фазы лунного затмения
Представление о прямолинейных световых лучах используется в инструментальной оптике для конструирования и расчета оптических приборов (рис. 1.7).
Рис. 1.7. Прямолинейный ход световых лучей в оптических приборах
Слайд 23
Расходящийся пучок лучей, выходящих из одной точки (гомоцентрический
пучок лучей), с помощью оптической системы (линзы, объектива, вогнутого
зеркала) можно превратить в сходящийся. Точка пересечения этих сходящихся лучей будет действительным изображением соответствующей точки источника (предмета). Изображение протяженного предмета, формируемое оптической системой, представляет собой центральную проекцию предмета. Центр проекции находится в центре входного зрачка оптической системы. Для фотообъектива центр проекции обычно совпадает с центром диафрагмы объектива.
Физическая реализация геометрического проектирования с
помощью световых лучей, т.е. формирование оптических
изображений, широко используется в технике, в частности, при
создании печатных микросхем (рис. 1.8).
Слайд 24
Тщательные эксперименты показали, однако, что закон прямолинейного распространения
света нарушается, если свет проходит через очень малые отверстия,
причем отклонение от прямолинейности распространения тем больше, чем меньше отверстия. Это мы увидим и обсудим в дальнейшем.
Рис. 1.8. Изображенные на фотопленке элементы микросхемы проецируются на кристалл кремния, где получается подобное уменьшенное (с помощью системы линз) изображение микросхемы. Специальная обработка позволяет превратить это изображение в печатную микросхему
Другим примером, где геометрическая оптика допускает непрямолинейное распространение света, являются оптически неоднородные среды (рис. 1.9.)
Слайд 25
Рис. 1.9. Геометрическая оптика допускает искривление лучей света
в оптически неоднородных средах.
На приведенном рисунке показатель преломления
вещества в полусфере зависит от расстояния до ее центра по формуле n = n0 / (1 + (r/r0)2). Луч, падающий нормально на расстоянии r0 от центра полусферы, выйдет с другой стороны полусферы на том же расстоянии от центра
Слайд 26
1.2.2. Независимость световых лучей
Закон независимости световых пучков:
эффект,
производимый отдельным пучком, не
зависит от того, действуют ли одновременно
остальные
пучки или они устранены.
Разбивая световой поток на отдельные световые пучки (например, с
помощью диафрагм), можно показать, что действие выделенных
световых пучков независимо.(рис. 1.10).
Рис. 1.10. Производимое одним пучком действие не зависит от наличия других пучков
Слайд 27
Рис. 1.11
Если свет падает на границу раздела двух
сред (двух прозрачных веществ), то падающий луч (рис.1.11) разделяется
на два — отраженный II и преломленный III, направления которых задаются законами отражения и преломления.
Закон независимости световых лучей следует из линейности уравнений электродинамики (уравнений Максвелла). Этот закон строго справедлив для вакуума.
Для световых лучей в веществе закон независимости лучей справедлив для линейных сред, оптические свойства которых не зависят от интенсивности света. Это выполняется точно при небольшой и приближенно при умеренной интенсивности света.
Этот закон нарушается при распространении в веществе света
высокой интенсивности.
Слайд 28
Закон отражения:
отраженный луч лежит в одной плоскости
с падающим лучом и перпендикуляром, проведенным к границе раздела
двух сред в точке падения.
1.2.3. Отражение света
По основной идее геометрической оптики свет распространяется между двумя точками по прямой линии. Пусть свет на своем пути наталкивается на какой-то объект (рис. 1.12), например зеркало. В этом случае справедлив закон: свет, попадая на зеркало, не проходит через него, а отражается и снова уходит по прямой линии,
Слайд 29
Рис. 1.12. Угол падения равен углу отражения. S1
- отражающая поверхность; S2 - плоскость падения; АО -
падающий луч; ОВ - отраженный луч; ON - нормаль к отражающей поверхности.
причем направление прямой меняется при изменении наклона зеркала. Соотношение между этими двумя углами очень простое: падающий на зеркало луч после отражения движется по такому пути, что углы между каждым лучом и зеркалом равны. Углы удобно отсчитывать от нормали к поверхности зеркала.
Закон отражения имеет вид i = .
Слайд 30
Более сложный закон имеет место при переходе света
из одной среды в другую, например, из воздуха в
воду; здесь тоже свет движется, но не по прямой. Траектория луча в воде образует некоторый угол с траекторией в воздухе.
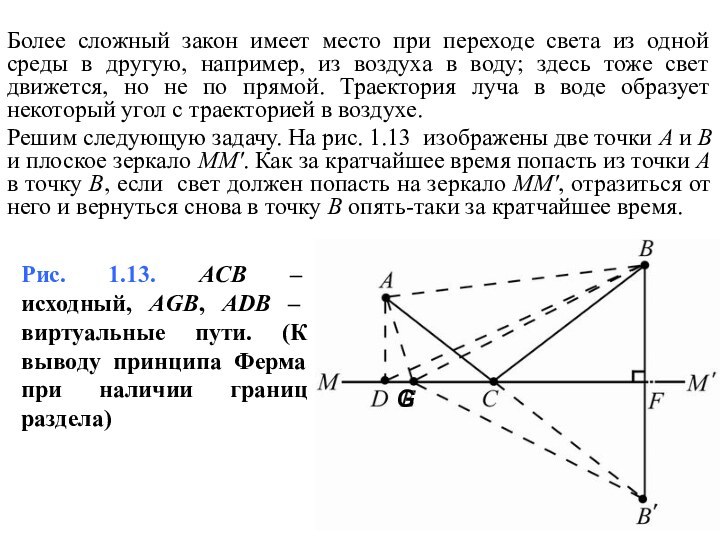
Решим следующую задачу. На рис. 1.13 изображены две точки А и В и плоское зеркало ММ'. Как за кратчайшее время попасть из точки А в точку В, если свет должен попасть на зеркало ММ', отразиться от него и вернуться снова в точку В опять-таки за кратчайшее время.
Рис. 1.13. ACB – исходный, АGВ, АDВ – виртуальные пути. (К выводу принципа Ферма при наличии границ раздела)
G
Слайд 31
Воспользуемся для этого геометрическим приемом. По другую сторону
зеркала ММ', на таком же расстоянии от него, что
и точка В, построим точку В'. Проведем линию GВ'. Угол BFM прямой и BF = FB', GB=GВ'. Сумма длин отрезков АG + GВ равна сумме длин AG + GВ'.
G
Рис. 1.13.
Сумма длин АG + GВ будет наименьшей, когда точка С будет лежать на прямой, соединяющей А и В'. Другими словами, нужно идти к мнимой точке В' (мнимому изображению точки В), и тогда мы найдем точку С. Если АСВ' – прямая линия, то угол BCF равен углу B'CF и углу АСМ. Утверждение о равенстве углов падения и отражения равносильно утверждению, что свет при отражении от зеркала в точку В выбирает путь, требующий наименьшего
Слайд 32
времени. Еще Герон Александрийский высказал утверждение, что свет
при отражении идет из одной точки в другую по
кратчайшему пути.
При отражении от плоской зеркальной поверхности световых
лучей, исходящих от некоторого предмета, возникает мнимое
изображение предмета (рис. 1.14). Предмет и его мнимое
изображение располагаются симметрично относительно зеркальной
поверхности. Изображение предмета в плоском зеркале равно по
размеру самому предмету. Пучок лучей, выходящих из точечного
Рис. 1.14
источника (т.е. гомоцентрический пучок), после отражения в плоском зеркале остается гомоцентрическим: если отраженные лучи мысленно продолжить назад, эти продолжения лучей пересекутся за зеркалом в одной точке, которую можно считать
Слайд 33
мнимым изображением источника. Источник и его изображение расположены
симметрично относительно зеркала. Наблюдателю кажется что отраженные от зеркала
лучи выходят из точки S',
расположенной за зеркалом симметрично точке S.
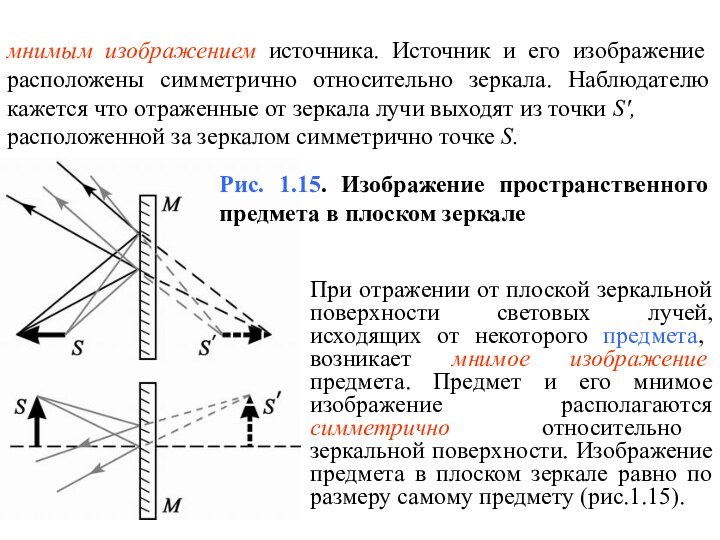
Рис. 1.15. Изображение пространственного предмета в плоском зеркале
При отражении от плоской зеркальной поверхности световых лучей, исходящих от некоторого предмета, возникает мнимое изображение предмета. Предмет и его мнимое изображение располагаются симметрично относительно зеркальной поверхности. Изображение предмета в плоском зеркале равно по размеру самому предмету (рис.1.15).
Слайд 34
Мнимое изображение пространственного (трехмерного) предмета в плоском зеркале
отличается от самого предмета, как правая система координат отличается
от левой (т.е. как правая рука отличается от левой).
1.2.4. Преломление света
При падении света на границу раздела прозрачных сред с
показателями преломления n1 и n2 часть света отражается, а часть
проходит во вторую среду, изменяя направление распространения
(преломляется) (рис. 1.11).
Рис. 1.11. Схема хода лучей
при преломлении
Слайд 35
Закон преломления:
луч падающий, луч преломленный и перпендикуляр,
проведенный к границе раздела в точке падения, лежат в
одной плоскости.
Угол падения и угол отражения равны друг другу:
Отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред:
1.2.1
Слайд 36
где n21 — относительный показатель преломления второй среды
относительно первой.
1.2.2
Учитывая (1.2.2), закон преломления (1.2.1) можно записать
в виде
Математическую формулировку этого закона дал Декарт.
Из симметрии выражения (1.1.3) вытекает обратимость световых
n1 sin i1 = n2 sin i2.
1.2.3
Слайд 37
лучей. Если обратить луч III (рис. 1.5), заставив
его падать на границу раздела под углом i2, то
преломленный луч в первой среде будет распространяться под углом i1, т. е. пойдет в обратном направлении вдоль луча I.
Если свет распространяется из среды с большим показателем преломления п1 (оптически более плотной) в среду с меньшим показателем преломления п2 (оптически менее плотную) (п1 > п2), например из стекла в воду, то, согласно (1.1.3),
Рис.1.16
Слайд 38
и преломленный луч удаляется от нормали и угол
преломления i2 больше, чем угол падения i1 (рис. 1.16,
а ). С увеличением угла падения увеличивается угол преломления (рис. 1.16, б, в ), до тех пор пока при некотором угле падения (i1 = iпр) угол преломления не окажется равным π/2. Угол iпр называется предельным углом. При углах падения i > inp весь падающий свет полностью отражается (рис. 1.16, г ).
Рис.1.16
Слайд 39
По мере приближения угла падения к предельному интенсивность
преломленного луча уменьшается, а отраженного — растет (рис. 1.16,
а — в). Если i1 = iпр, то интенсивность преломленного луча обращается в нуль, а интенсивность отраженного равна интенсивности падающего (рис. 1.16, г). Таким образом, при углах падения в пределах от iпр до π/2 луч не преломляется, а полностью отражается в первую среду, причем интенсивности отраженного и падающего лучей одинаковы.
Это явление называется полным отражением.
Предельный угол inp определим из формулы (1.1.3) при подстановке в нее i2 = π /2. Тогда
1.2.5. Полное отражение света
Слайд 40
1.1.4,а
Уравнения (1.1.4) удовлетворяет значениям угла inp при п2
< п1 Следовательно,
явление полного отражения имеет место только
при падении света из среды оптически более плотной в среду оптически менее плотную.
n1 sin iпред = n2 sin π/2 = n2.
Откуда получаем (n1 > n2 )
iпред = arcsin (n2 /n1).
1.1.4,б
Рис. 1.16,г. При переходе из оптически более плотной среды 1 в оптически менее плотную 2 свет может полностью отразиться от границы раздела и не попасть в среду 2 – явление полного внутреннего отражения
Слайд 41
Полное внутреннее отражение используется для передачи света и
изображения по пучкам гибких волокон световодам. Основной элемент
световода стеклянное волокно цилиндрической формы, покрытое оболочкой из прозрачного материала с меньшим, чем у волокна, показателем преломления (рис. 1.171.19).
Рис. 1.17. Этот телефонный провод содержит 144 оптические нити
Рис. 1.18. За счет многократного полного отражения свет может быть направлен по любому прямому или изогнутому пути
Рис. 1.19. Свет, проходящий по оптическим световодам, выглядит как миниатюрный фейерверк
Рис. 1.20. Так выглядит через эндоскоп язва желудка
Слайд 42
Световоды используются при создании телеграфно-телефонных кабелей большой емкости.

Кабель состоит из сотен и тысяч оптических волокон, тонких,
как человеческий волос. По такому кабелю, толщиной в обычный карандаш, можно одновременно передавать до восьмидесяти тысяч телефонных разговоров (рис. 1.17).
Волоконнооптический зонд (эндоскоп) дает врачам возможность исследовать желудочно-кишечный тракт и другие внутренние области организма. Изображения, получаемые зондом, затем передаются на телевизионный экран (рис. 1.20).
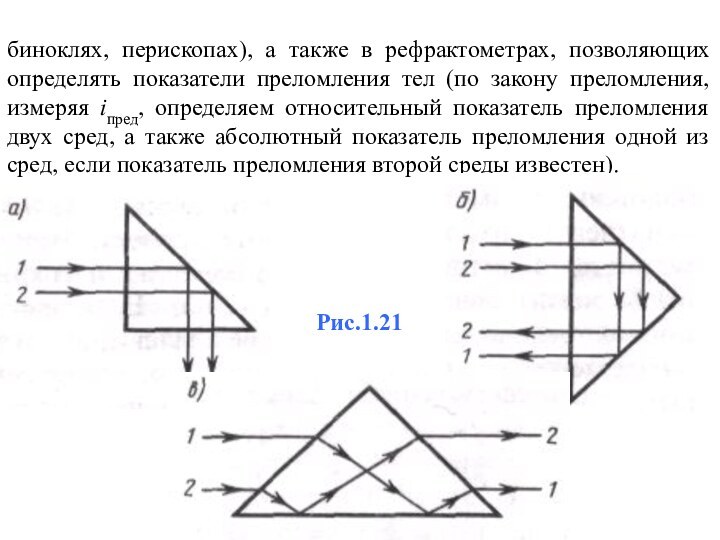
Явление полного отражения используется в призмах полного отражения. Показатель преломления стекла равен n 1.5, поэтому предельный угол для границы стекло - воздух inpед = arcsin (1/1.5) = 42°. Поэтому при падении света на границу стекло — воздух при i > 42° всегда будет иметь место полное отражение. На рис. 1.21, а — в показаны призмы полного отражения, позволяющие: а) повернуть луч на 90°; б) повернуть изображение: в) обернуть лучи. Такие призмы применяются в оптических приборах (например, в
Слайд 43
биноклях, перископах), а также в рефрактометрах, позволяющих определять
показатели преломления тел (по закону преломления, измеряя iпред, определяем
относительный показатель преломления двух сред, а также абсолютный показатель преломления одной из сред, если показатель преломления второй среды известен).
Рис.1.21