Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Открытый урок по теме Симметрия 8 класс.

Содержание

2. Симметрия вокруг нас.Симметрия геометрических фигур.Построение фигур, симметричных данным.Симметрия вокруг нас.Симметрия геометрических фигур.Построение фигур, симметричных данным.План
3. СИММЕТРИЯ ВОКРУГ НАС
4. Симметрия является фундаментальным свойством природы,
5. Виды симметрии.1 Центральная симметрия - симметрия относительно
6. С симметрией мы встречаемся всюду - в
7. Симметрия в кристаллах
8. Своим развитием учение о симметрии
9. Каждая снежинка- это маленький кристалл замерзшей
10. Простые на первый взгляд снежинки столь же
11. Снежинки сохраняют сложную форму на протяжении всего
12. Симметрия в мире живой природы
13. Так, бабочка симметрична по отношению к отражению
15. Достаточно взглянуть на растения,
17. Переходя от одного поколения данного растения к
18. Для растений характерна симметрия конуса, которая хорошо видна на примере фактически любого дерева.
19. Симметрия в искусстве
20. Симметрия как объективный признак красоты проходит через всю историю искусств.
21. Прекрасные образцы симметрии демонстрируют произведения архитектуры.
22. Симметрия прослеживается почти во всех стилях и направлениях архитектуры.
24. В средние века возник ГОТИЧЕСКИЙ стиль. Готические
25. Все здания, построенные в стиле КЛАССИЦИЗМ, имеют четкие прямолинейные формы и симметричные композиции.
26. Архитекторы Возрождения создали стиль - РЕНЕССАНС, в
27. Много примеров использования симметрии дает старая русская архитектура:колокольни, сторожевые башни, внутренние опорные столбы.
28. Симметрия, воспринимаемая человеком как закономерность структуры, как
29. Симметрия в технике
30. Технические объекты - самолеты, мосты, автомашины, ракеты,
31. В технике красота, соразмерность механизмов часто бывает
33. В технике существует своего рода
34. Но именно противоборство, а часто и единство
35. Например, строители современных мостов, высотных зданий, башен
36. Примером удивительного сочетания симметрии и асимметрии является
37. Симметрия геометрических фигур
38. Определение осевой симметрииДве точки А и А1
39. Равнобедренный треугольникАСВ
40. РомбАВСD
41. ПрямоугольникАВСD
42. Квадрат.KLMN
43. Равнобедренная трапеция.FRST
44. ОкружностьO
45. ПараллелограммАСВDEFGHO
46. Определение центральной симметрииДве точки А и А1
47. Построение фигур, симметричных данным.
48. LADCBEB1C1D1A1E1Построение фигуры, симметричной данной относительно оси симметрии
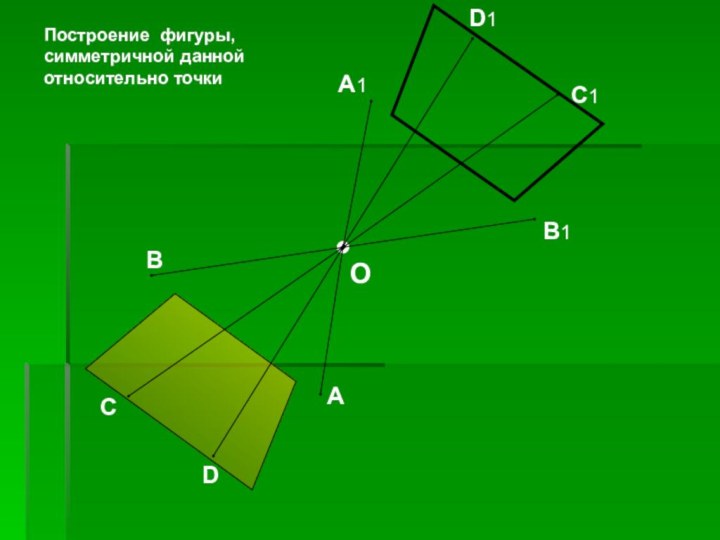
49. BACDB1A1C1D1OПостроение фигуры, симметричной данной относительно точки
50. Домашнее задание
52. Скачать презентацию
53. Похожие презентации

Симметрия вокруг нас.Симметрия геометрических фигур.Построение фигур, симметричных данным.Симметрия вокруг нас.Симметрия геометрических фигур.Построение фигур, симметричных данным.План

Главная
Геометрия
Открытый урок по теме Симметрия 8 класс.

Симметрия вокруг нас.Симметрия геометрических фигур.Построение фигур, симметричных данным.Симметрия вокруг нас.Симметрия геометрических фигур.Построение фигур, симметричных данным.План

Симметрия является фундаментальным свойством природы, представление о котором, как отмечал

Виды симметрии.1 Центральная симметрия - симметрия относительно точки. 2 Осевая симметрия –

С симметрией мы встречаемся всюду - в природе, технике, искусстве, науке, например,

Своим развитием учение о симметрии обязано в первую очередь естествоиспытателям,

Каждая снежинка- это маленький кристалл замерзшей воды. Форма снежинок может быть

Простые на первый взгляд снежинки столь же уникальны как и человеческая личность

Снежинки сохраняют сложную форму на протяжении всего пути, сохраняя при этом симметрию.

Так, бабочка симметрична по отношению к отражению в воображаемом зеркале, разделяющем

Открытый урок по теме Симметрия 8 класс.

Достаточно взглянуть на растения, и мы увидим строго симметричные

Переходя от одного поколения данного растения к другому, наблюдается сохранение определенных свойств.

Для растений характерна симметрия конуса, которая хорошо видна на примере фактически любого дерева.

Симметрия как объективный признак красоты проходит через всю историю искусств.

Прекрасные образцы симметрии демонстрируют произведения архитектуры. Большинство зданий зеркально симметричны. Общие

Симметрия прослеживается почти во всех стилях и направлениях архитектуры.

В средние века возник ГОТИЧЕСКИЙ стиль. Готические здания отличаются обилием ажурных, как

Все здания, построенные в стиле КЛАССИЦИЗМ, имеют четкие прямолинейные формы и симметричные композиции.

Архитекторы Возрождения создали стиль - РЕНЕССАНС, в котором использовали наследие античного искусства,

Много примеров использования симметрии дает старая русская архитектура:колокольни, сторожевые башни, внутренние опорные столбы.

Симметрия, воспринимаемая человеком как закономерность структуры, как внешнее проявление внутреннего порядка, начинает

Технические объекты - самолеты, мосты, автомашины, ракеты, молотки, гайки - практически все

В технике красота, соразмерность механизмов часто бывает связана с их надежностью, устойчивостью

В технике существует своего рода постулат: наиболее целесообразные и функционально

Но именно противоборство, а часто и единство двух великих начал - симметрии

Например, строители современных мостов, высотных зданий, башен знают, что конструкция не должна

Примером удивительного сочетания симметрии и асимметрии является храм Василия Блаженного на Красной

Определение осевой симметрииДве точки А и А1 называются симметричными относительно прямой а,

Определение центральной симметрииДве точки А и А1 называются симметричными относительно точки О,

LADCBEB1C1D1A1E1Построение фигуры, симметричной данной относительно оси симметрии

BACDB1A1C1D1OПостроение фигуры, симметричной данной относительно точки

Слайды презентации

Слайд 2 Симметрия вокруг нас.
Симметрия геометрических фигур.
Построение фигур, симметричных данным.

Симметрия

вокруг нас.
Симметрия геометрических фигур.
Построение фигур, симметричных данным.

План

Слайд 3 СИММЕТРИЯ ВОКРУГ НАС

Слайд 4 Симметрия является фундаментальным свойством природы, представление

о котором, как отмечал академик В. И. Вернадский (1863—1945),

«слагалось в течение десятков, сотен, тысяч поколений".

Первоначальное понятие о геометрической симметрии как о гармонии пропорций, как о "соразмерности'' (что и означает в переводе с греческого слово "симметрия'') с течением времени приобрело универсальный характер и было осознано как всеобщая идея неизменности относительно некоторых прeобразований. Таким образом, геометрический объект или физическое явление считаются симметричными, если с ними можно сделать что-то такое, после чего они останутся неизменными.

Что такое симметрия?

Слайд 5 Виды симметрии.
1 Центральная симметрия - симметрия относительно точки.

2 Осевая симметрия – симметрия относительно прямой.
3 Зеркальная

симметрия - симметрия относительно плоскости (в биологии - билатеральная).
4 Поворотная симметрия или поворот вокруг точки или оси.
5 Скользящая симметрия или параллельный перенос вдоль прямой.
6 Винтовая симметрия – это поворот и параллельный перенос одновременно.

Слайд 6 С симметрией мы встречаемся всюду - в природе,

С симметрией мы встречаемся всюду - в природе, технике, искусстве, науке,

технике, искусстве, науке, например, симметрия, свойственная бабочке и кленовому

листу, симметрия форм автомобиля и самолета, симметрия в ритмическом построении стихотворения, симметрия атомной структуры молекул и кристаллов.

С симметрией мы встречаемся всюду - в природе, технике, искусстве, науке, например, симметрия, свойственная бабочке и кленовому листу, симметрия форм автомобиля и самолета, симметрия в ритмическом построении стихотворения, симметрия атомной структуры молекул и кристаллов.

Слайд 7 Симметрия в кристаллах

Слайд 8 Своим развитием учение о симметрии обязано

в первую очередь естествоиспытателям, углубленно изучавшим кристаллические образования, это:

И. Кеплер, Н. Стенон, П. Кюри.

И. Кеплер

П.Кюри

Слайд 9 Каждая снежинка- это маленький кристалл замерзшей воды.

Каждая снежинка- это маленький кристалл замерзшей воды. Форма снежинок может

Форма снежинок может быть очень разнообразной, но все они

обладают симметрией.

Слайд 10 Простые на первый взгляд снежинки столь же уникальны

Простые на первый взгляд снежинки столь же уникальны как и человеческая

как и человеческая личность — на свете не найти

двух одинаковых. Не бывает пятиугольных или семиугольных снежинок. Все снежинки имеют строго шестиугольную форму.

Слайд 11 Снежинки сохраняют сложную форму на протяжении всего пути,

Снежинки сохраняют сложную форму на протяжении всего пути, сохраняя при этом

сохраняя при этом симметрию. Обращаясь к аналогиям в симметрии

шестиугольных пчелиных сот и зерен граната, ученые открывает некоторые особенности этой формы. Например, из всех правильных геометрических фигур только треугольники, квадраты и шестиугольники могут заполнить плоскость, не оставляя пустот, причем правильный шестиугольник покрывает наибольшую площадь. Ученые делают вывод, что форма сот и зерен обусловлена не природой их вещества и не внешними обстоятельствами, а уже заложена в них.

Мир неживой природы — это прежде всего мир симметрии, придающей его творениям устойчивость и красоту.

Слайд 12 Симметрия в мире живой природы

Слайд 13 Так, бабочка симметрична по отношению к отражению в

воображаемом зеркале, разделяющем
бабочку пополам вдоль ее туловища.

Симметричны
формы жука, листа, цветка и т.д.

Слайд 14

Слайд 15
Достаточно взглянуть на растения, и мы

увидим строго симметричные цветы и листья, многие плоды и

даже сами растения с их симметрично-винтовым расположением листьев на стержне ствола.

Слайд 16

Слайд 17 Переходя от одного поколения данного растения к другому,

Переходя от одного поколения данного растения к другому, наблюдается сохранение определенных

наблюдается сохранение определенных свойств. Так из семечка вырастает новый

подсолнух (подсолнечник) с таким же огромным соцветием-корзинкой, также исправно поворачивающимся к Солнцу. Это тоже есть симметрия, ее обычно называют наследственностью.

Слайд 18
Для растений характерна симметрия конуса, которая хорошо

видна на примере фактически любого дерева.

Слайд 19 Симметрия в искусстве

Слайд 20 Симметрия как объективный признак красоты проходит через всю

историю искусств.

Слайд 21 Прекрасные образцы симметрии демонстрируют произведения архитектуры. Большинство

Прекрасные образцы симметрии демонстрируют произведения архитектуры. Большинство зданий зеркально симметричны.

зданий зеркально симметричны. Общие планы построек, фасады, орнаменты, карнизы,

колонны обнаруживают соразмерность, гармонию.

Слайд 22 Симметрия прослеживается почти во всех стилях и

направлениях архитектуры.

Слайд 23

Слайд 24 В средние века возник ГОТИЧЕСКИЙ стиль. Готические здания

В средние века возник ГОТИЧЕСКИЙ стиль. Готические здания отличаются обилием ажурных,

отличаются обилием ажурных, как кружева, украшений, скульптур, орнаментов, поэтому

и снаружи, и внутри они производят впечатление легкости и воздушности. Фасады сооружений обладают зеркальной (осевой) симметрией.

Слайд 25 Все здания, построенные в стиле КЛАССИЦИЗМ, имеют четкие

прямолинейные формы и симметричные композиции.

Слайд 26 Архитекторы Возрождения создали стиль - РЕНЕССАНС, в котором

Архитекторы Возрождения создали стиль - РЕНЕССАНС, в котором использовали наследие античного

использовали наследие античного искусства, греческие архитектурные ордеры. Здания в

стиле ренессанс строги по форме, с четкими прямыми линиями. Сохраняется симметрия фасадов

Слайд 27 Много примеров использования симметрии дает старая русская архитектура:
колокольни,

сторожевые башни, внутренние опорные столбы.

Слайд 28 Симметрия, воспринимаемая человеком как закономерность структуры, как внешнее

Симметрия, воспринимаемая человеком как закономерность структуры, как внешнее проявление внутреннего порядка,

проявление внутреннего порядка, начинает обладать эстетической ценностью, т.е. воспринимается

как красота.

Слайд 29 Симметрия в технике

Слайд 30 Технические объекты - самолеты, мосты, автомашины, ракеты, молотки,

Технические объекты - самолеты, мосты, автомашины, ракеты, молотки, гайки - практически

гайки - практически все они от мала до велика

обладают той или иной симметрией.

Слайд 31 В технике красота, соразмерность механизмов часто бывает связана

В технике красота, соразмерность механизмов часто бывает связана с их надежностью,

с их надежностью, устойчивостью в работе. Симметричная форма дирижабля,

самолета, подводной лодки, автомобиля и т.д. обеспечивает хорошую обтекаемость воздухом или водой, а значит, и минимальное сопротивление движению

Слайд 32

Слайд 33 В технике существует своего рода постулат:

наиболее целесообразные и функционально совершенные изделия являются наиболее красивыми.

В подтверждение этого постулата приведем слова генерального авиаконструктора О.К. Антонова: "Мы прекрасно знаем, что красивый самолет летает хорошо, а некрасивый плохо, а то и вообще не будет летать. Это не суеверие, а совершенно материалистическое положение... конструктор может идти часто от красоты к технике, от решений эстетических к решениям техническим".

Слайд 34 Но именно противоборство, а часто и единство двух

Но именно противоборство, а часто и единство двух великих начал -

великих начал - симметрии и асимметрии, во многом определяют

гармонию природы, мудрость науки и красоту искусства. Мы живем, находясь под воздействием с одной стороны, симметрии и необходимого, а с другой - асимметрии и случайности и используя в своей практике диалектику симметрии - асимметрии.

«Сфера влияния'' симметрии поистине безгранична: природа - искусство - техника.

Слайд 35 Например, строители современных мостов, высотных зданий, башен знают,

Например, строители современных мостов, высотных зданий, башен знают, что конструкция не

что конструкция не должна быть безупречно симметричной из-за опасности

возникновения резонансных колебаний, которые могут привести к ее разрушению. Поэтому симметрию конструкций сознательно нарушают, вводя в нее отдельные асимметричные элементы. Т. е. Чистая симметрия может оказаться опасной. Она неустойчива.

Слайд 36 Примером удивительного сочетания симметрии и асимметрии является храм

Примером удивительного сочетания симметрии и асимметрии является храм Василия Блаженного на

Василия Блаженного на Красной площади в Москве. Эта причудливая

композиция из десяти храмов, каждый из которых обладает центральной симметрией, в целом не имеет ни зеркальной, ни поворотной симметрии. Симметричные архитектурные детали собора кружатся в своем асимметричном, беспорядочном танце вокруг его центрального шатра. Без своей удивительной асимметрии храм Василия Блаженного просто немыслим!

Слайд 37 Симметрия геометрических фигур

Слайд 38 Определение осевой симметрии
Две точки А и А1 называются

Определение осевой симметрииДве точки А и А1 называются симметричными относительно прямой

симметричными относительно прямой а, если эта прямая проходит через

середину отрезка АА1 и перпендикулярна к нему.
Фигура называется симметричной относительно оси а, если для каждой точки фигуры симметричная ей точка относительно оси а также принадлежит этой фигуре.

А1

Прямая а- ось симметрии фигуры

Слайд 39 Равнобедренный треугольник

А
С
В

Слайд 40 Ромб

А
В
С
D

Слайд 41 Прямоугольник

А
В
С
D

Слайд 42 Квадрат.

K
L
M
N

Слайд 43 Равнобедренная трапеция.

F
R
S
T

Слайд 44 Окружность

O

Слайд 45 Параллелограмм

А
С
В
D
E
F
G
H
O

Слайд 46 Определение центральной симметрии
Две точки А и А1 называются

Определение центральной симметрииДве точки А и А1 называются симметричными относительно точки

симметричными относительно точки О, если отрезок, их соединяющий, делится

точкой О пополам.
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.

А1

Точка О- центр симметрии фигуры