- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
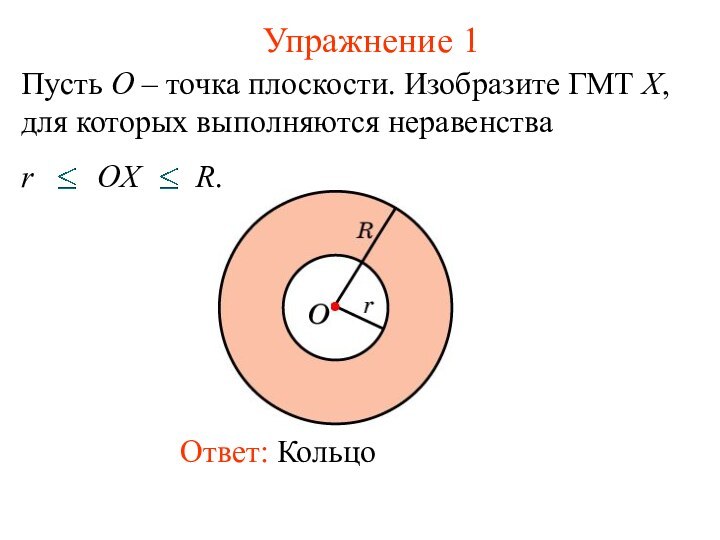
Презентация на тему Геометрические места точек
Содержание
- 2. Упражнение 1Ответ: Кольцо
- 3. Упражнение 2На данной прямой a найдите точки,
- 4. На прямой c отметьте точки, удаленные от
- 5. Пересечение фигурПусть Ф1 и Ф2 – фигуры
- 6. Упражнение 4Ответ: Искомое ГМТ является пересечением двух
- 7. Объединение фигурПусть Ф1 и Ф2 – фигуры
- 8. Упражнение 5Даны две точки O1 и O2.
- 9. Разность фигурПусть Ф1 и Ф2 – фигуры
- 10. Упражнение 6Ответ: Искомое ГМТ является разностью двух
- 11. Серединный перпендикулярСерединным перпендикуляром к заданному отрезку называется
- 12. Упражнение 7Постройте геометрическое место точек, равноудаленных от точек A и B.
- 13. На прямой c отметьте точку C равноудаленную от точек A и B. Упражнение 8
- 14. Упражнение 9Найдите геометрическое место центров окружностей, проходящих
- 15. Упражнение 10Найдите геометрическое место вершин С равнобедренных
- 16. Упражнение 11Пусть А и В - точки
- 17. Упражнение 12Пусть А и В точки плоскости,
- 18. Упражнение 13Даны три точки: А, В, С.
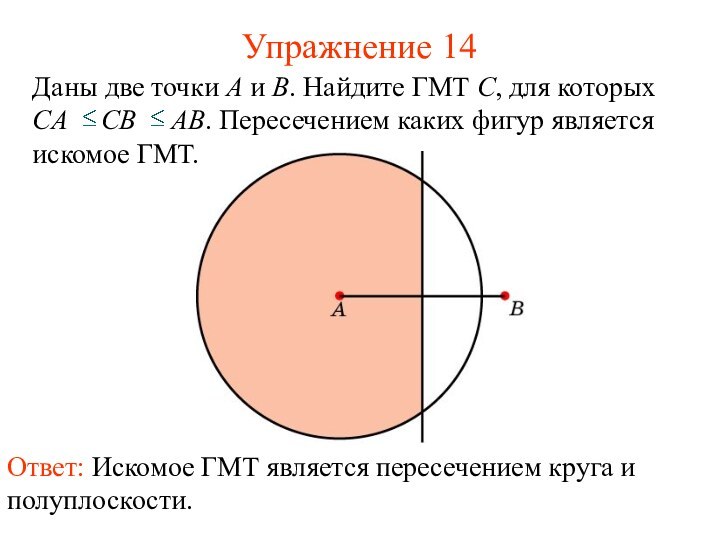
- 19. Упражнение 14Ответ: Искомое ГМТ является пересечением круга и полуплоскости.
- 20. Упражнение 15Даны три точки A, B, C.
- 21. Упражнение 16Даны три точки A, B, C.
- 22. Биссектриса углаТеорема. Биссектриса угла является ГМТ, лежащих
- 23. Постройте геометрическое место внутренних точек угла AOB, равноудаленных от его сторон. Упражнение 17
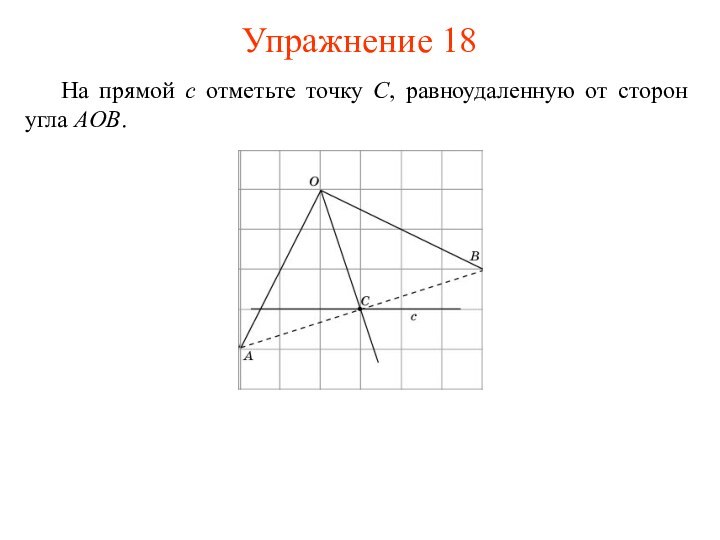
- 24. На прямой c отметьте точку C, равноудаленную от сторон угла AOB. Упражнение 18
- 25. Упражнение 19Что является геометрическим местом центров окружностей
- 26. Упражнение 20Ответ: а) Точки, принадлежащие биссектрисам четырех
- 27. Упражнение 21На прямой c, пересекающей стороны угла,
- 28. Скачать презентацию
- 29. Похожие презентации


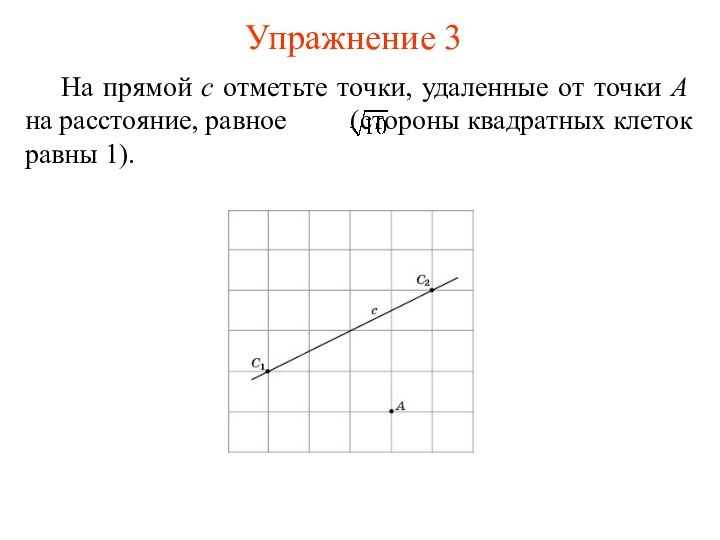













Слайд 4 На прямой c отметьте точки, удаленные от точки
A на расстояние, равное (стороны
квадратных клеток равны 1).Упражнение 3
Слайд 5
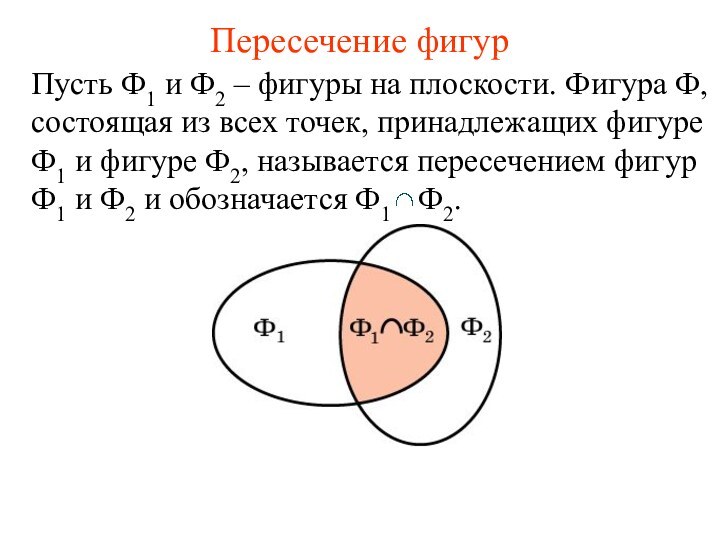
Пересечение фигур
Пусть Ф1 и Ф2 – фигуры на
плоскости. Фигура Ф, состоящая из всех точек, принадлежащих фигуре
Ф1 и фигуре Ф2, называется пересечением фигур Ф1 и Ф2 и обозначается Ф1 Ф2.
Слайд 6
Упражнение 4
Ответ: Искомое ГМТ является пересечением двух кругов
с центрами в точках O1, O2 и радиусами R1,
R2.Даны две точки O1 и O2. Найдите ГМТ X, для которых XO1 R1 и XO2 R2. Пересечением каких фигур является искомое ГМТ.
Слайд 7
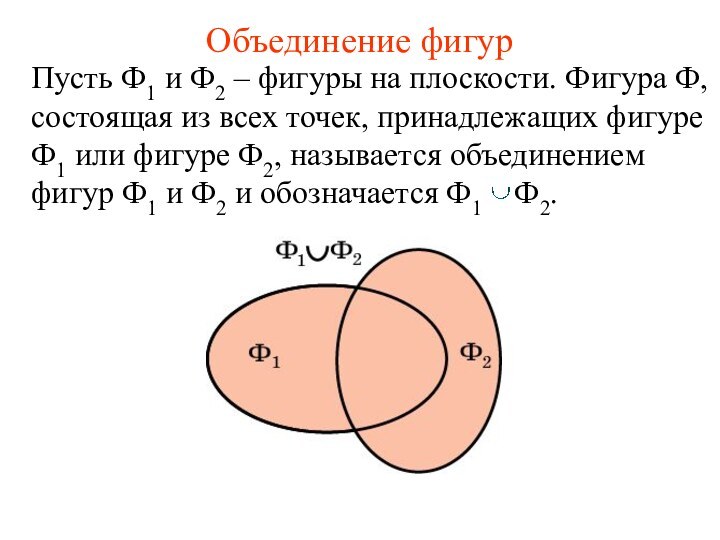
Объединение фигур
Пусть Ф1 и Ф2 – фигуры на
плоскости. Фигура Ф, состоящая из всех точек, принадлежащих фигуре
Ф1 или фигуре Ф2, называется объединением фигур Ф1 и Ф2 и обозначается Ф1 Ф2.
Слайд 8
Упражнение 5
Даны две точки O1 и O2. Найдите
ГМТ X, для которых
XO1 R1 или XO2 R2. Объединением каких фигур является искомое ГМТ.Ответ: Искомое ГМТ является объединением двух кругов с центрами в точках O1, O2 и радиусами R1, R2.
Слайд 9
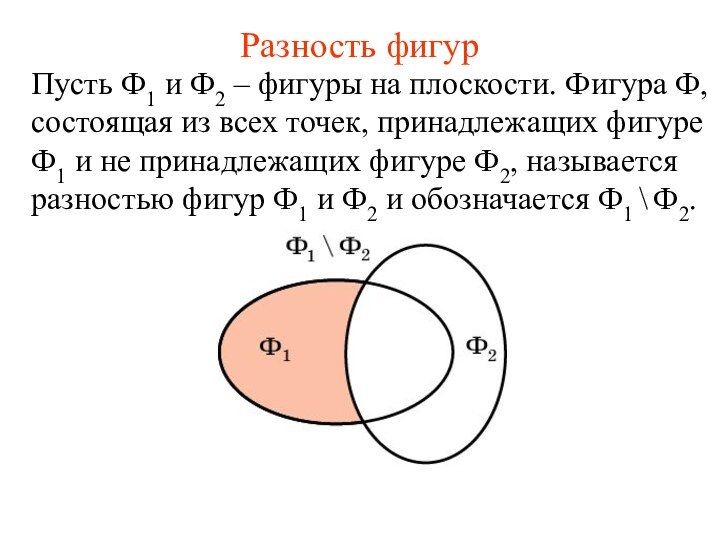
Разность фигур
Пусть Ф1 и Ф2 – фигуры на
плоскости. Фигура Ф, состоящая из всех точек, принадлежащих фигуре
Ф1 и не принадлежащих фигуре Ф2, называется разностью фигур Ф1 и Ф2 и обозначается Ф1 \ Ф2.
Слайд 10
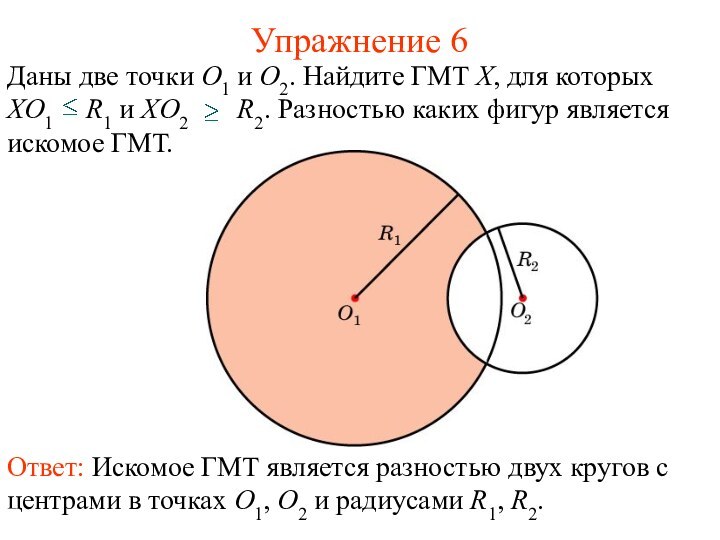
Упражнение 6
Ответ: Искомое ГМТ является разностью двух кругов
с центрами в точках O1, O2 и радиусами R1,
R2.Даны две точки O1 и O2. Найдите ГМТ X, для которых XO1 R1 и XO2 R2. Разностью каких фигур является искомое ГМТ.
Слайд 11
Серединный перпендикуляр
Серединным перпендикуляром к заданному отрезку называется …
Теорема.
Серединный перпендикуляр к отрезку является ГМТ, одинаково удаленных от
концов этого отрезка.Доказательство. Пусть дан отрезок АВ и точка О – его середина. Очевидно, точка О одинаково удалена от точек А, В и принадлежит серединному перпендикуляру. Пусть точка С одинаково удалена от точек А и В и не совпадает с точкой О.
Обратно, пусть точка С принадлежит серединному перпендикуляру и не совпадает с О, тогда прямоугольные треугольники АОС и ВОС равны (по катетам). Следовательно, АС=ВС.
Тогда треугольник АВС равнобедренный и СО – медиана. По свойству равнобедренного треугольника медиана является также и высотой. Значит, точка С принадлежит серединному перпендикуляру.
Слайд 14
Упражнение 9
Найдите геометрическое место центров окружностей, проходящих через
две данные точки.
Ответ: Серединный перпендикуляр к отрезку, соединяющему две
данные точки.
Слайд 15
Упражнение 10
Найдите геометрическое место вершин С равнобедренных треугольников
с заданным основанием AB.
Ответ: Серединный перпендикуляр к отрезку AB
без середины этого отрезка.
Слайд 16
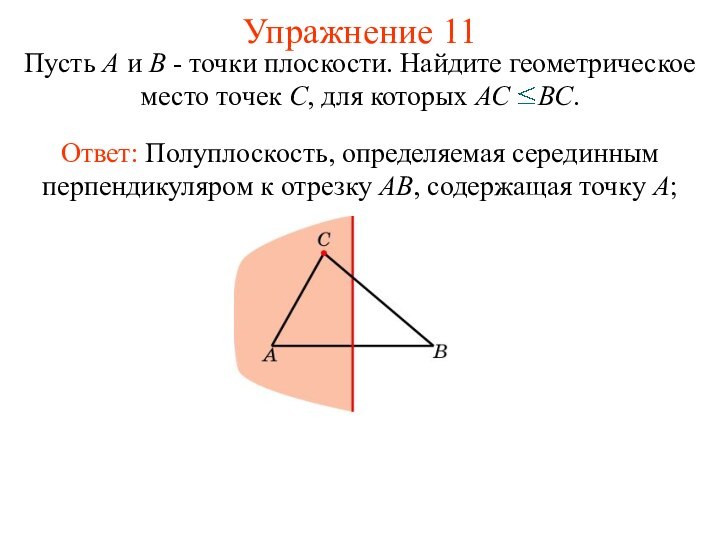
Упражнение 11
Пусть А и В - точки плоскости.
Найдите геометрическое место точек С, для которых АС
ВС.
Слайд 17
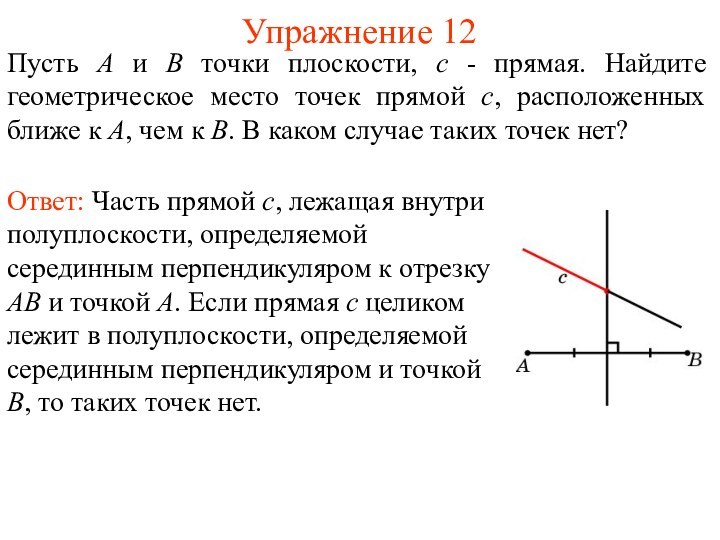
Упражнение 12
Пусть А и В точки плоскости, c
- прямая. Найдите геометрическое место точек прямой c, расположенных
ближе к А, чем к В. В каком случае таких точек нет?
Слайд 18
Упражнение 13
Даны три точки: А, В, С. Найдите
точки, которые одинаково удалены от точек А и В
и находятся на расстоянии R от точки С.
Слайд 20
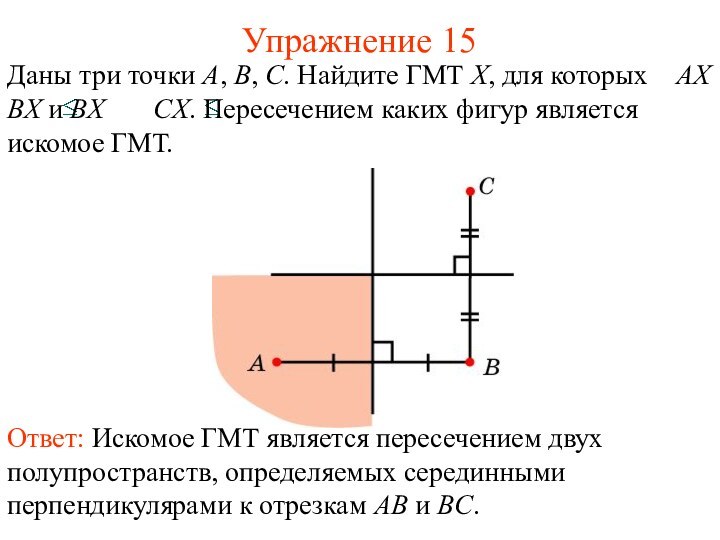
Упражнение 15
Даны три точки A, B, C. Найдите
ГМТ X, для которых AX
BX и BX CX. Пересечением каких фигур является искомое ГМТ.Ответ: Искомое ГМТ является пересечением двух полупространств, определяемых серединными перпендикулярами к отрезкам AB и BC.
Слайд 21
Упражнение 16
Даны три точки A, B, C. Найдите
ГМТ X, для которых AX
BX или BX CX. Объединением каких фигур является искомое ГМТ.Ответ: Искомое ГМТ является объединением двух полупространств, определяемых серединными перпендикулярами к отрезкам AB и BC.
Слайд 22
Биссектриса угла
Теорема. Биссектриса угла является ГМТ, лежащих внутри
этого угла и одинаково удаленных от его сторон.
Доказательство. Рассмотрим
угол c вершиной в точке О и сторонами а, b. Пусть точка С лежит внутри данного угла. Опустим из нее перпендикуляры СА и CB на стороны а и b. Если CA = CB, то прямоугольные треугольники АOС и ВOС равны (по гипотенузе и катету). Следовательно, углы AOC и BOC равны. Значит, точка C принадлежит биссектрисе угла. Обратно, если точка C принадлежит биссектрисе угла, то прямоугольные треугольники AOC и BOC равны (по гипотенузе и острому углу). Следовательно, AC = BC. Значит, точка С одинаково удалена от сторон данного угла.
Слайд 23
Постройте геометрическое место внутренних точек угла AOB, равноудаленных
от его сторон.
Упражнение 17
Слайд 25
Упражнение 19
Что является геометрическим местом центров окружностей касающихся
двух данных пересекающихся прямых?
Ответ: Биссектрисы углов, образующихся при пересечении
данных прямых, без точки пересечения этих прямых.
Слайд 26
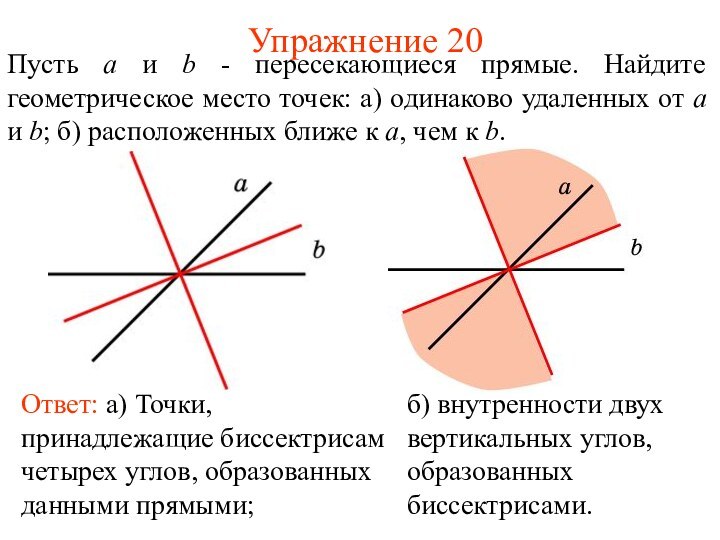
Упражнение 20
Ответ: а) Точки, принадлежащие биссектрисам четырех углов,
образованных данными прямыми;
б) внутренности двух вертикальных углов, образованных
биссектрисами. Пусть a и b - пересекающиеся прямые. Найдите геометрическое место точек: а) одинаково удаленных от a и b; б) расположенных ближе к a, чем к b.