Слайд 2
Актуальность
Математика – предмет, изучающийся с первого по выпускной
класс. Объем материала, терминов, которыми должен оперировать старшеклассник по
математике, чрезвычайно велик. Необходимо знать и уметь применят такие методы для решения задач, которые позволят сэкономить время и будут наглядны, т.е. решение задачи будет выглядеть очевидным. Многие задачи алгебры очень трудно решить аналитическим путем. Поэтому любое представление условия задачи в виде рисунка или чертежа облегчает решение задачи. Многие задачи ЕГЭ из части 2 можно решить геометрическим методом.
Геометрический метод состоит в том, что само доказательство или решение задачи направляется наглядным представлением.
Слайд 3
В своей работе мы ставим следующую цель:
Показать, что
преимущество геометрического решения алгебраических задач в его наглядности, так
как геометрический подход допускает изящное решение;
Слайд 4
Задачи:
Найти и изучить литературу по данной теме.
Рассмотреть
алгебраические задачи, которые можно решить и алгебраически и геометрически.
Сравнить способы решения задач различными методами.
Определить задачи, которые удобнее решать геометрическим методом.
Рассмотреть ряд приемов решения нестандартных и конкурсных задач.
Развивающая задача: повысить свое интеллектуальное развитие.
Слайд 5
Предмет исследования: Геометрические методы решения задач.
Объект исследования: Алгебраические
задачи.
Методы исследования: Аналогия, обобщение, анализ научной литературы.
Слайд 6
Основная часть
1. Решение тригонометрических задач.
Многие тригонометрические задачи
не решаются привычными для них методами или решаются очень
сложно, а использование какого-нибудь геометрического приема дает короткое решение. «Тригонометрические функции — это испытанный аппарат геометрии и их тоже нужно излагать, отправляясь от простых наглядных задач, как они практически и возникли — из решения треугольников»?
Слайд 7
Пример 1: выразить
через
все остальные аркфункции
РЕШЕНИЕ: Так как то
можно рассматривать как радианную меру острого угла прямоугольного треугольника, в котором противолежащий ему катет а=7, гипотенуза с=√50
По теореме Пифаго-
ра другой катет
равен:
а
b
c
α
Слайд 8
Угол α можно рассматривать как арккосинус или арктангенс,
или арккотангенс соответствующих чисел (рис. 4).
a
b
c
α
Слайд 9
Пример 2. Вычислить arctg2+arctg3+arctg1
Определение: arctg а (арктангенс а)
— это такое число из интервала тангенс которого равен
а.
Решение: На основании этого определения arctg1= π/4 Что же такое arctg2 ?
Это число из интервала (-π/2:π/2) тангенс которого равен 2. Аналогично и arctg3.
Воспользуемся графической интерпретацией (рис.5). Из рисунка видно, что arctg2 = x1 , arctg3 = x2 .
Ясно, что числа х1 и х2 иррациональные и указать их значения можно только приближенно. По рис. 6 видно, что arctg2= α, а arctg3 = β. Однозначно определить ответ невозможно.
x1
x2
Слайд 10
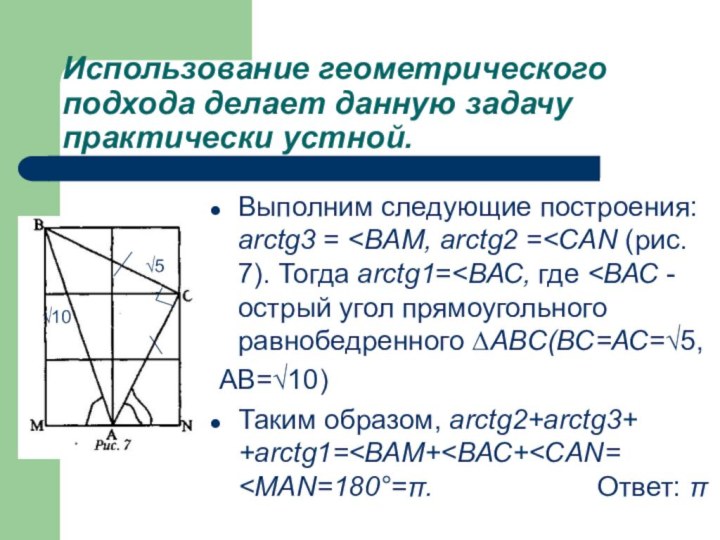
Использование геометрического подхода делает данную задачу практически устной.
Выполним
следующие построения: arctg3 =
Тогда arctg1=<ВАС, где <ВАС - острый угол прямоугольного равнобедренного ∆ABC(ВС=АС=√5,
АВ=√10)
Таким образом, arctg2+arctg3+ +arctg1=<ВАМ+<ВАС+
√5
√10
Слайд 11
2. Решение систем уравнений
Решить систему уравнений:
Решение: По
теореме обратной теореме Пифагора, из уравнения х²+у²=3², числа х
и у являются катетами ∆АBD (
Слайд 12
По теореме обратной теореме о пропорциональных отрезках
) = = 5, тогда
AB²=AD•AC, 9=х•5, х =9/5
BC²=DC•AC, 16=z•5, z =16/5
BD²=y²=x•z =9/5•16/5 и BD=12/5=y.
Однако, такой прием дает потерю корней, легко убедиться, что х=±9/5; у=±12/5; z=±16/5.
Слайд 13
3. Решение текстовых задач на движение
Задачи на движение
и на совместную работу можно решать графически. Решение задачи
основывается на точных геометрических соотношениях.
Решить задачу: Расстояние между двумя городами равно 450 км. Два автомобиля выходят одновременно навстречу друг другу. Один автомобиль мог бы пройти все расстояние за 9 часов, другой – вдвое быстрее. Через сколько часов они встретятся?
Читаем с чертежа ответ: 3 часа.
Слайд 14
4. Решение конкурсных задач и задач ЕГЭ
Геометрическим методом
хорошо решаются уравнения и неравенства с параметрами, а также
их системы
Пример1: При каком a система уравнений |x|+|y| =1
имеет ровно четыре решения? x²+y²=a
Решение: Построим линии, определяе-
мые уравнениями системы.
r=√2/2. Четыре решения могут быть
только в двух случаях,
когда a=R²=1, или a=r²=1/2.
Ответ:1;1/2.
Слайд 15
Пример 2.
При каких значениях a система уравнений
x²+y²=z; имеет
x+y+z=a единственное решение?
Система имеет единственное решение тогда и только тогда, когда уравнение x²+y²+x+y=a, полученное из системы
x²+y²= z
x+y+z=a
Слайд 16
Преобразуем полученное уравнение:
x²+y²+x+y=(x²+x+0,25)+(y²+y+0,25)-0,25-0,25=a
(x+0,5)²+(y+0,5)²=0,5+a (*)
Итак, уравнение(*) задает на плоскости
окружность с центром(-0,5;0,5)и радиусом R=√0,5+a.
1)Если 0,5+а
множество точек, задаваемых на плоскости уравнением(*), пусто, а следовательно, исходная система решений не имеет
Слайд 17
2)Если 0,5+а=0, т.е. при а=-0,5, уравнение(*) имеет единственное
решение, т.к. и окружность вырождается в точку(-0,5;0,5);
3)Если 0,5+a>0,т.е. при
a>-0,5, множество точек, задаваемых на плоскости уравнением (*), является окружностью с центром(-0,5;0,5) и R√0,5+а. В этом случае уравнение (*), а следовательно, и исходная система, имеет бесконечно много решений.
Ответ: а = - 0,5.
Слайд 18
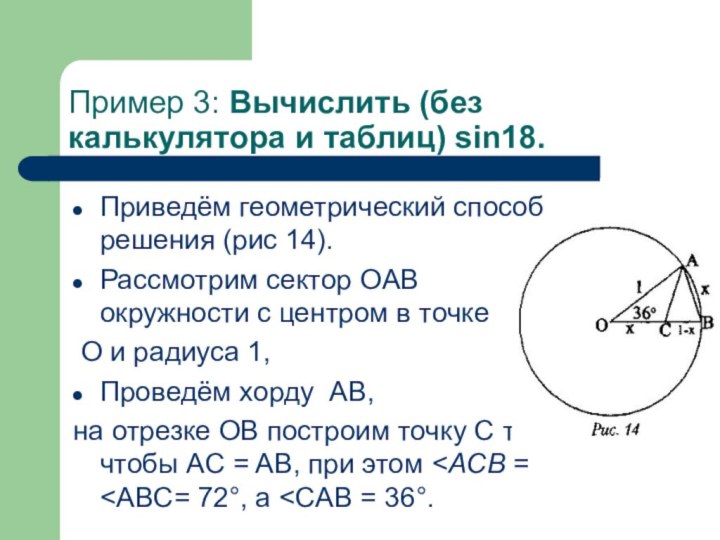
Пример 3: Вычислить (без калькулятора и таблиц) sin18.
Приведём
геометрический способ решения (рис 14).
Рассмотрим сектор OAB окружности с
центром в точке
O и радиуса 1,
Проведём хорду AB,
на отрезке OB построим точку C так, чтобы AC = AB, при этом
Слайд 19
Таким образом OC = AC.
Пусть AB = x,
СВ = 1-x.
Поскольку АС – биссектриса треугольника ОАВ, справедлива
пропорция = откуда
х²+х-1=0, (х>0), х=(√ 5-1)/2
По теореме косинусов: АВ²=ОА²+ОВ² -2ОА·ОВ · cos<АОВ, х²=1+1 – 2cos36°,
х=√2(1-cos36°) =√2(1-cos²18°+sin²18°)= 2sin18°
Тогда sin 18°=(√ 5-1)/4
Ответ: (√ 5-1)/4
72°
Слайд 20
Пример 4: Решить уравнение sin3x + 2√2cos3x =
2
Решение: Рассмотрим прямоугольный треугольник с катетами
ВС = 1
и АС = 2√2. Тогда АВ= = 3. Пусть <А= φ, где φ – острый угол.
Тогда cos φ=2√2/3 и sin φ=1/3.
Имеем sin3x+ cos3x = , cos3xcos φ + sin3x sin φ= сos(3x- φ)=
Решая уравнение получим: х=1/3arcsin1/3±1/3arccos2/3+2πn/3, nєZ
Ответ: х=1/3arcsin1/3±1/3arccos2/3+2πn/3, nєZ
3
2√2
1
Слайд 21
Пример 5: Найдите значение выражения
tg(arcsin ).
Решение: По определению арксинуса имеем:
-
arc . Построим прямоугольный
треугольник АВС с углом А, который равен arcsin . При этом, по теореме Пифагора, прилежащий катет будет равен . Поэтому tg(arcsin ) = = и tg(arcsin )= · =2.
Ответ: 2.
А
В
С
2
5
ЗАКЛЮЧЕНИЕ
Геометрический метод характеризуют как метод, идущий от наглядных
представлений. Существенными признаками этого понятия являются геометрические (наглядные) представления и законы геометрии, в которых отражены свойства геометрических фигур.
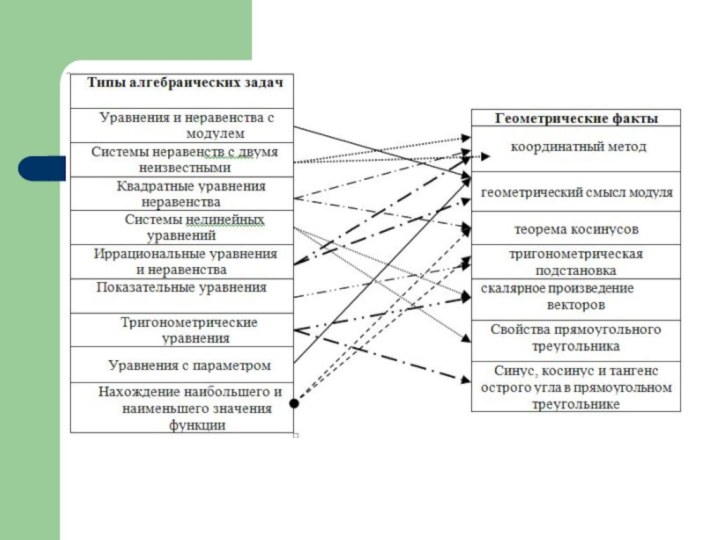
Мы попытались сопоставить задачи и способы их решения, вот какая картина у нас получилась:
Слайд 24
Мы предлагаем свой алгоритм решения алгебраических задач геометрическим
способом:
Построение геометрической модели задачи, т.е. перевод её на язык
геометрии;
Решение получившейся геометрической задачи;
Перевод полученного ответа с геометрического языка на естественный.
Слайд 25
Преимущества решения задач геометрическим способом:
При решении задачи этим
методом четко определяется начало действия;
Графическая иллюстрация облегчает проведение
анализа, составления уравнений, помогает найти несколько способов решения;
Расширяется область использования графиков, повышается графическая культура учеников;
Совершенствуется техника решения уравнений (разделений переменных);
Реализуются внутрипредметные (алгебра и геометрия) и межпредметные (математика и физика) связи.
Выводы
Мы рассмотрели различные задачи, подобрали для
них геометрические способы решения, сравнили алгебраический и геометрический методы решения.
Удобнее и нагляднее всего решать геометрическим методом тригонометрические задачи. Этот метод можно использовать в качестве проверки при решении задач.
Рассмотренные геометрические методы подходят для решения конкурсных нестандартных и олимпиадных задач. Позволяют существенно упростить их решение, сделать его более понятным и наглядным.
Применение геометрических методов позволяет развивать пространственное воображение, которое является основным для освоения материала в старших классах. Позволяет сократить время решения задач (применимо к тестам).
Слайд 27
Литература:
Куликова Л. В. , Литвинова С. А., За
страницами учебника математики, М. - Глобус, 2008.
Киселева Ю. С.,
Методическое пособие по теме: Использование геометрических методов при решении алгебраических задач.
В.А. Филимонов, Геометрия помогает решить задачу – Математика в школе № 2-3, 1992
Ш.А. Алимов, Ю.М. Колягин, Ю. В. Сидоров и др., Алгебра и начало анализа: Учеб. Для 10-11 кл. образоват. учреждений ,– 10-е изд., дораб. – М.: Просвящение, 2002. – 384с.