Презентация на тему по геометрии. 11 класс. Конус.

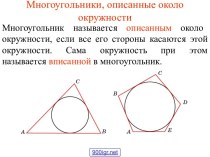
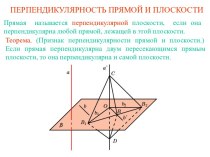
становление александрийской математики (геометрической алгебры) как науки.
В XI книге

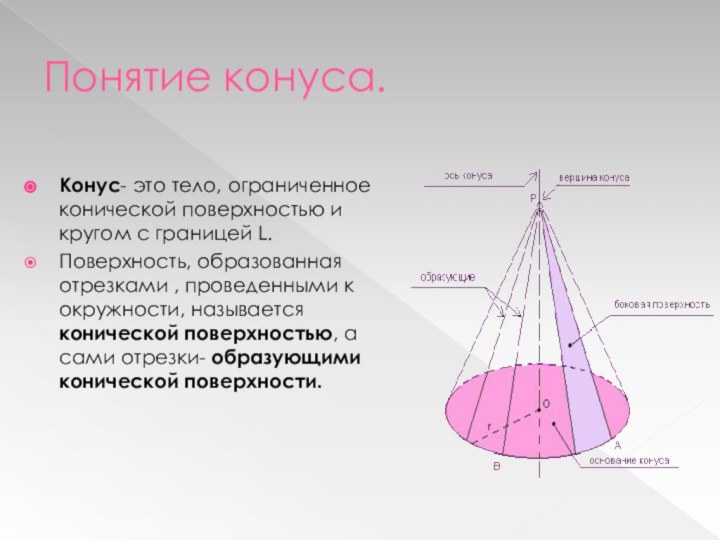
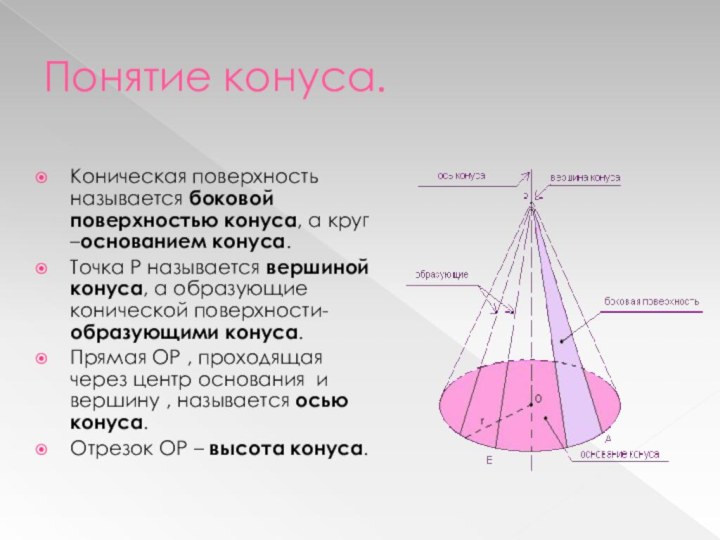
«Начал» дается следующее определение: если вращающийся около одного из своих катетов прямоугольный треугольник слева вернется в то же самое положение, из которого он начал двигаться, то описанная фигура будет конусом.

Евклид рассматривает  только прямые конусы, т.е. такие, у которых ось перпендикулярна к основанию.

ЕВКЛИД
(330-275гг. до н.э.)

и астроном, ученик Евклида дал полное изложение теории и

основанных им трудов «Конические сечения» в восьми книгах.

У Евклида нет понятия конической поверхности, оно было введено Аполлонием в его “Конических сечениях”, при этом он имел в виду обе плоскости конуса.

АПОЛЛОНИЙ ПЕРГСКИЙ

(260-170гг.до н. э.)

для вывода формулы  объема конуса и изложенных в пяти

предложениях 12 книги “Начал” Евклида, дал Евдокс Книдский.

ЕВДОКС КНИДСКИЙ
(408 - З55 гг.до.н.э )

и механик, основоположник теоретической механики и гидростатики.

В «Началах»

Евклида мы находим определение только объёмов цилиндра и конуса, площадь же боковых поверхностей была найдена Архимедом.

До нас дошло тринадцать трактатов Архимеда. В самом знаменитом из них — «О шаре и цилиндре» он доказал следующую теорему: «Поверхность всякого равнобедренного (т.е. прямого кругового) конуса, за вычетом основания, равна кругу, радиус которого есть средняя пропорциональная между стороной (т.е. образующей) конуса и радиуса круга, являющегося основанием конуса». 

АРХИМЕД (около 287 до н.э., Сиракузы,  Сицилия — 212 до н.э)

кругом с границей L.
Поверхность, образованная отрезками , проведенными к

окружности, называется конической поверхностью, а сами отрезки- образующими конической поверхности.

круг –основанием конуса.
Точка Р называется вершиной конуса, а образующие

конической поверхности- образующими конуса.
Прямая ОР , проходящая через центр основания и вершину , называется осью конуса.
Отрезок ОР – высота конуса.

катета АВ.

конуса, то
сечение представляет собой
равнобедренный треугольник,
основание которого- диаметр
основания конуса, а

боковые
стороны- образующие
конуса. Это сечение- осевое.

площадь ее развертки.
Площадь боковой поверхности конуса равна произведению половины

длины окружности основания на образующую.

Площадь полной поверхности конуса- сумма площадей боковой поверхности и основания.

Sбок. = П r l

Sкон.= П r (l+r)

другая называется усеченным конусом.
Основание исходного конуса и круг ,

полученный в сечении этого конуса плоскостью, называются основаниями усеченного конуса , а отрезок , соединяющий их центры ,-высотой усеченного конуса.

его боковой поверхностью, а отрезки образующих конической поверхности ,

заключенные между основаниями, называются образующими усеченного конуса.

вокруг стороны CD.

полусуммы длин окружностей оснований на образующую.

S = π (r

+ r1) l