стороне
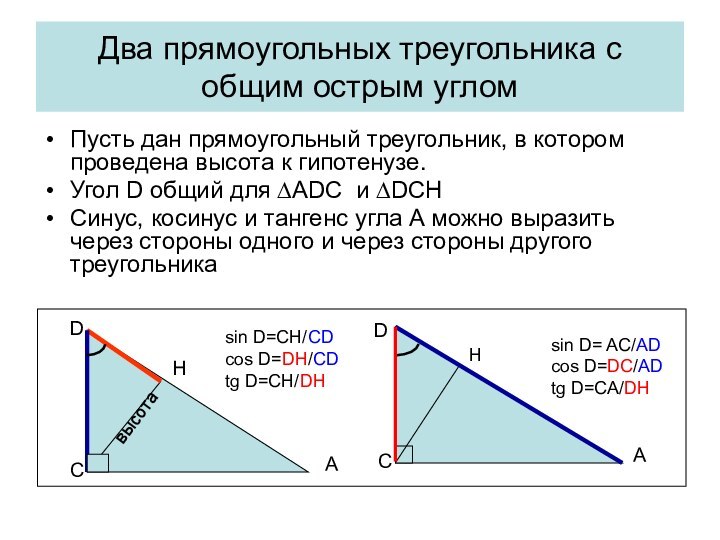
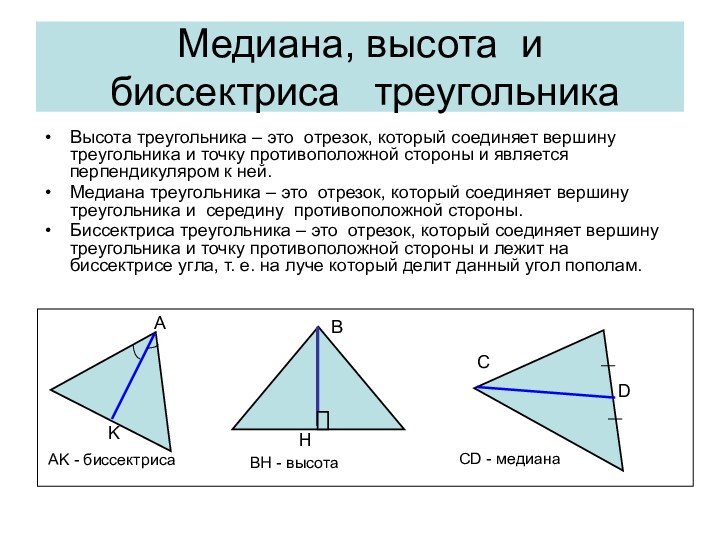
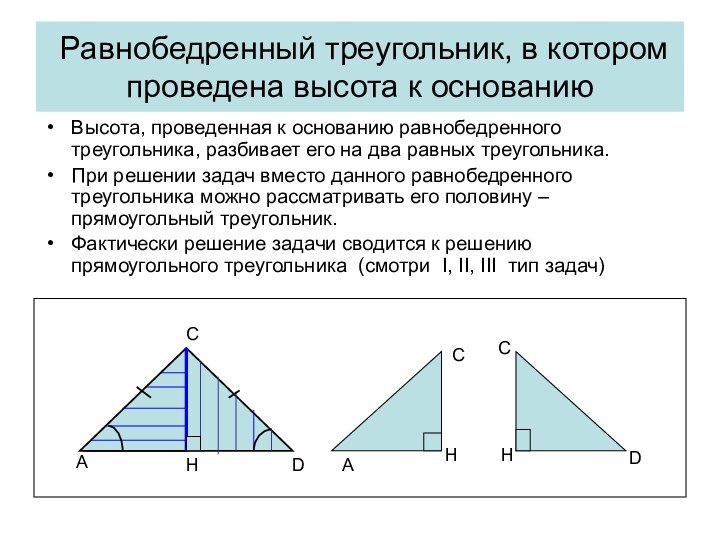
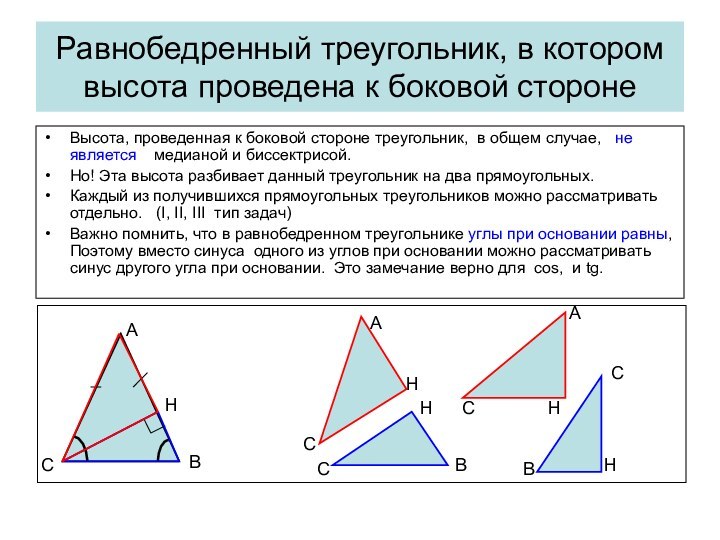
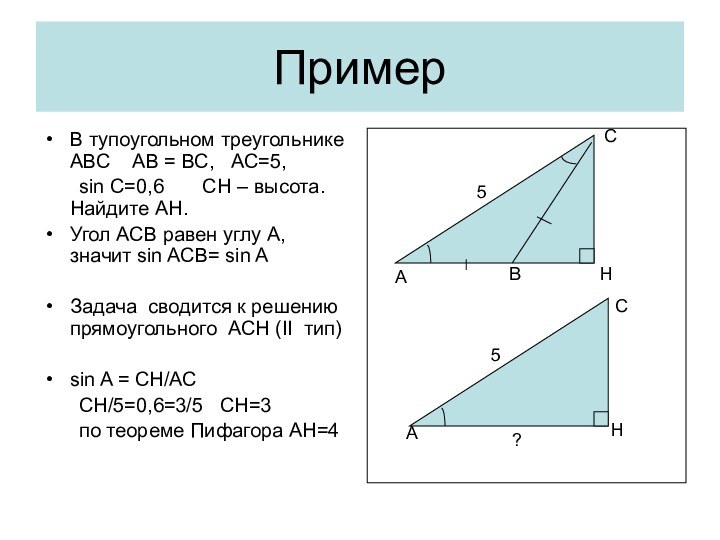
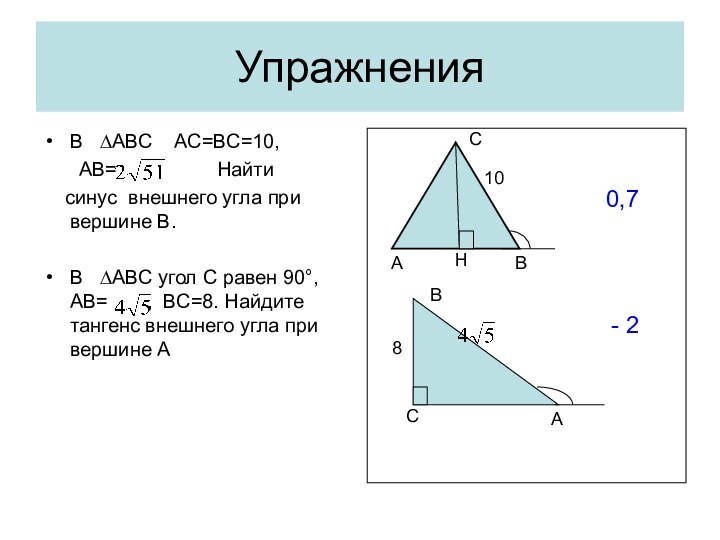
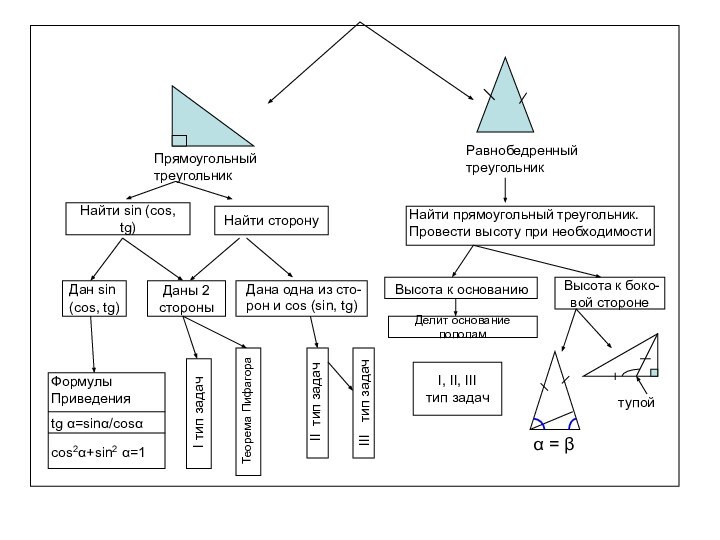
Высота, проведенная к боковой стороне треугольник, в общем случае,
не является медианой и биссектрисой.
Но! Эта высота разбивает данный треугольник на два прямоугольных.
Каждый из получившихся прямоугольных треугольников можно рассматривать отдельно. (I, II, III тип задач)
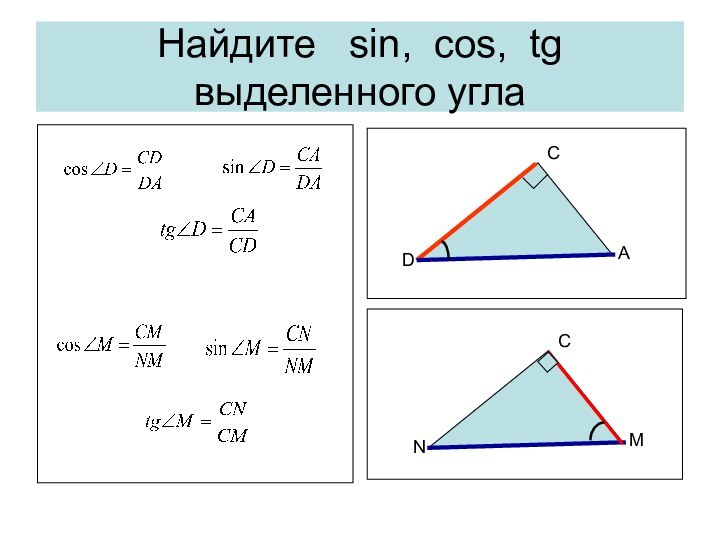
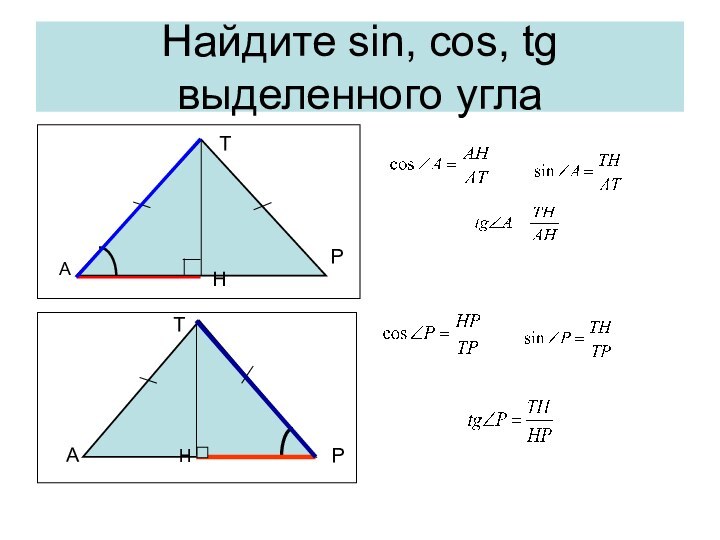
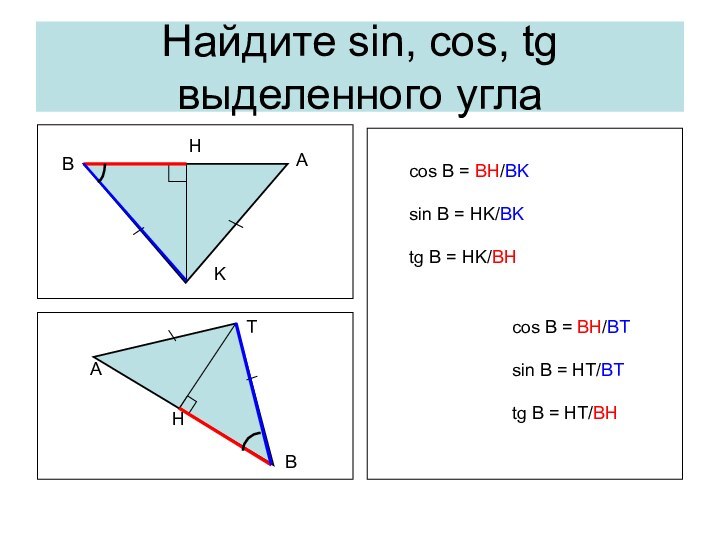
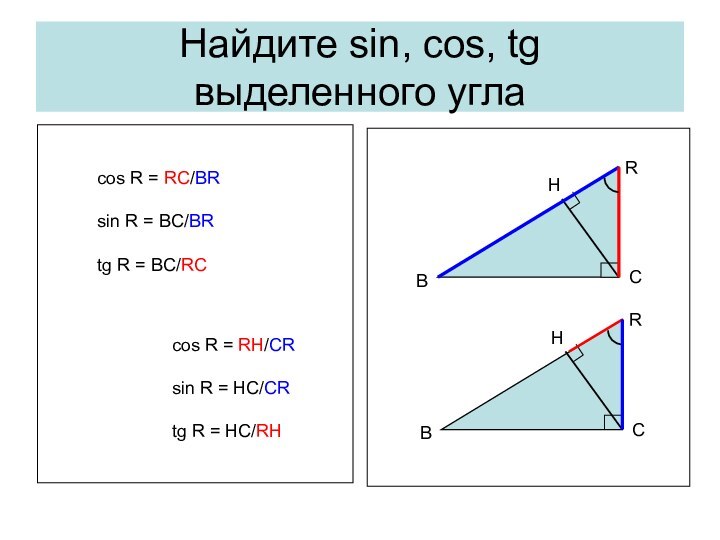
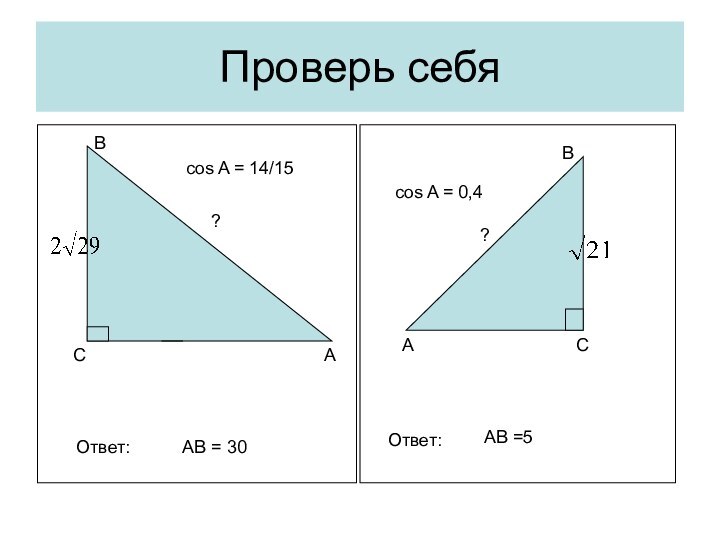
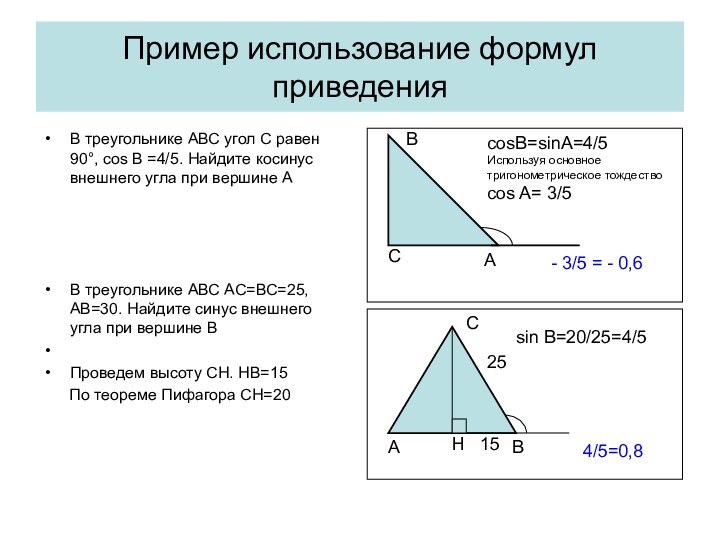
Важно помнить, что в равнобедренном треугольнике углы при основании равны, Поэтому вместо синуса одного из углов при основании можно рассматривать синус другого угла при основании. Это замечание верно для cos, и tg.
B
B
H
A
C
H
H
H
H
A
A
C
C
C
C
B