Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по теме четерыхугольники для итогового повторения в 9 классе

Содержание

ВИДЫ ЧЕТЫРЕХУГОЛЬНИКОВромбпрямоугольникквадратпараллелограммравнобокаяпроизвольный четырехугольниктрапецияпрямоу-гольная
ЧЕТЫРЕХУГОЛЬНИКИЧетырехугольником называется фигура, которая состоит из четырех точек (вершины) и четырех последовательно ВИДЫ ЧЕТЫРЕХУГОЛЬНИКОВромбпрямоугольникквадратпараллелограммравнобокаяпроизвольный четырехугольниктрапецияпрямоу-гольная ПРОИЗВОЛЬНЫЙ ЧЕТЫРЕХУГОЛЬНИКαβαδγ)Сумма внутренних углов равна:Площадь (через диагонали и угол между ними):adbcα + ЧЕТЫРЕХУГОЛЬНИК, ОПИСАННЫЙ ОКОЛО ОКРУЖНОСТИacbdrЧетырехугольник можно описать около окружности, если суммы противолежащих ЧЕТЫРЕХУГОЛЬНИК, ВПИСАННЫЙ В ОКРУЖНОСТЬACBDЧетырехугольник можно вписать в окружность, если сумма противолежащих ПАРАЛЛЕЛОГРАММСВСD abβ)Параллелограмм – это четырехугольник, противоположные стороны которого попарно параллельны.Сумма квадратов диагоналей ПРЯМОУГОЛЬНИКВСD abβ)Прямоугольник – это параллелограмм, у которого все углы прямые.Диагонали прямоугольника равны ОКРУЖНОСТЬ, ОПИСАННАЯ ОКОЛО ПРЯМОУГОЛЬНИКА abОколо любого прямоугольника можно описать окружность.Радиус описанной окружности РОМБ a АBCDРомб – это параллелограмм, у которого все ОКРУЖНОСТЬ, ВПИСАННАЯ В РОМБ a АBCDHВ любой ромб можно вписать КВАДРАТВСD aКвадратом называется прямоугольник , у которого все стороны равны.Диагонали квадрата равны, ОКРУЖНОСТИ КВАДРАТАВСD aОколо квадрата можно описать окружность. Радиус описанной окружности АdrRгде а
Слайды презентации

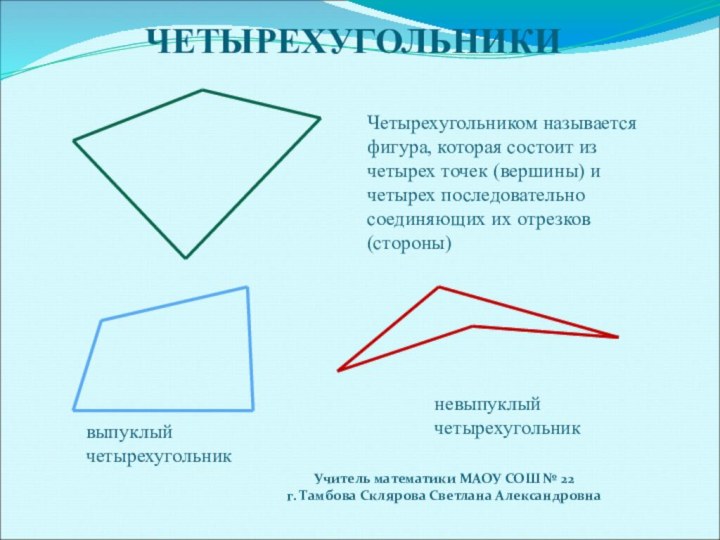
Слайд 2 ВИДЫ ЧЕТЫРЕХУГОЛЬНИКОВ
ромб
прямоугольник
квадрат
параллелограмм



равнобокая
произвольный четырехугольник
трапеция
прямоу-
гольная

ВИДЫ ЧЕТЫРЕХУГОЛЬНИКОВромбпрямоугольникквадратпараллелограммравнобокаяпроизвольный четырехугольниктрапецияпрямоу-гольная

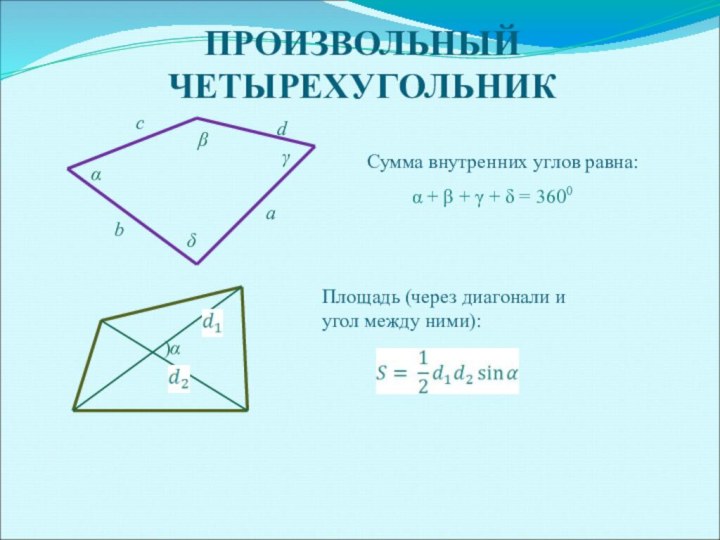
Слайд 3 ПРОИЗВОЛЬНЫЙ ЧЕТЫРЕХУГОЛЬНИК
α

β
α
δ

γ
)
Сумма внутренних углов равна:


Площадь (через диагонали и

ПРОИЗВОЛЬНЫЙ ЧЕТЫРЕХУГОЛЬНИКαβαδγ)Сумма внутренних углов равна:Площадь (через диагонали и угол между ними):adbcα

угол между ними):






a
d
b
c





α + β + γ + δ

= 3600

Слайд 4 ЧЕТЫРЕХУГОЛЬНИК, ОПИСАННЫЙ ОКОЛО ОКРУЖНОСТИ
a

c
b

d




r
Четырехугольник можно описать около

ЧЕТЫРЕХУГОЛЬНИК, ОПИСАННЫЙ ОКОЛО ОКРУЖНОСТИacbdrЧетырехугольник можно описать около окружности, если суммы

окружности, если суммы противолежащих сторон равны:
a + c

= b + d

Если четырехугольник описан около окружности, то суммы противолежащих сторон равны.





p – полупериметр, r – радиус вписанной окружности

Центр описанной окружности – точка пересечения биссектрис углов этого четырехугольника.

¬



Слайд 5
ЧЕТЫРЕХУГОЛЬНИК, ВПИСАННЫЙ В ОКРУЖНОСТЬ
A

C
B

D


Четырехугольник можно вписать в

ЧЕТЫРЕХУГОЛЬНИК, ВПИСАННЫЙ В ОКРУЖНОСТЬACBDЧетырехугольник можно вписать в окружность, если сумма

окружность, если сумма противолежащих углов равна :
Если

четырехугольник вписан в окружность, то суммы противолежащих углов равны 1800




α


β

δ

γ

α + γ = β + δ = 1800




Центр описанной окружности – точка пересечения серединных перпендикуляров к сторонам этого четырехугольника.
Произведение диагоналей вписанного четырехугольника равно сумме произведений противоположных сторон четырехугольника (теорема Птолемея):







,

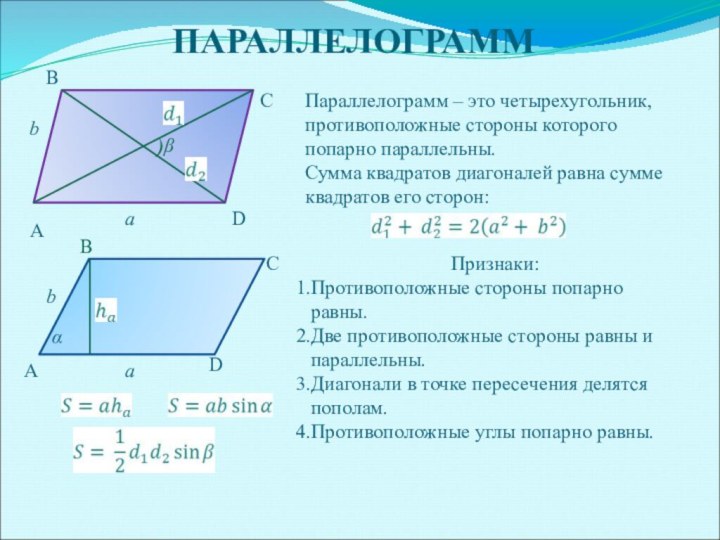
Слайд 6 ПАРАЛЛЕЛОГРАММ

С
В
С
D




a
b
β
)
Параллелограмм – это четырехугольник, противоположные стороны которого

ПАРАЛЛЕЛОГРАММСВСD abβ)Параллелограмм – это четырехугольник, противоположные стороны которого попарно параллельны.Сумма квадратов

попарно параллельны.
Сумма квадратов диагоналей равна сумме квадратов его сторон:


a
b
А
В
А
D






α




Признаки:
Противоположные стороны попарно равны.
Две противоположные стороны равны и параллельны.
Диагонали в точке пересечения делятся пополам.
Противоположные углы попарно равны.



Слайд 7 ПРЯМОУГОЛЬНИК

В
С
D




a
b
β
)
Прямоугольник – это параллелограмм, у которого все

ПРЯМОУГОЛЬНИКВСD abβ)Прямоугольник – это параллелограмм, у которого все углы прямые.Диагонали прямоугольника

углы прямые.
Диагонали прямоугольника равны
(AC = BD) и точкой

пересечения делятся пополам.


А







d



β

угол между диагоналями

проверь себя

Слайд 8
ОКРУЖНОСТЬ, ОПИСАННАЯ ОКОЛО ПРЯМОУГОЛЬНИКА




a
b
Около любого прямоугольника можно

ОКРУЖНОСТЬ, ОПИСАННАЯ ОКОЛО ПРЯМОУГОЛЬНИКА abОколо любого прямоугольника можно описать окружность.Радиус описанной

описать окружность.
Радиус описанной окружности R = OB








d


R


где d

– диагональ прямоугольника



D

C

B

A

O

Слайд 9
РОМБ




a



















РОМБ a АBCDРомб – это параллелограмм, у которого


А
B
C
D
Ромб – это параллелограмм, у которого все стороны равны.
Диагонали

в ромбе взаимно перпендикулярны, делятся в точке пересечения пополам и являются биссектрисами его углов.







)

α





r – радиус вписанной окружности






,


- диагонали

¬

Слайд 10
ОКРУЖНОСТЬ, ВПИСАННАЯ В РОМБ




a












ОКРУЖНОСТЬ, ВПИСАННАЯ В РОМБ a АBCDHВ любой ромб можно








А
B
C
D
H
В любой ромб можно вписать окружность. Радиус

вписанной окружности (r) удовлетворяет соотношениям:


r

L

h



, где h - высота ромба
a – его сторона


,

диагонали

Точка касания вписанной окружности делит сторону ромба на отрезки, связанные с его диагоналями и радиусом вписанной окружности следующими соотношениями:





L

L

Слайд 11 КВАДРАТ

В
С
D




a
Квадратом называется прямоугольник , у которого все

КВАДРАТВСD aКвадратом называется прямоугольник , у которого все стороны равны.Диагонали квадрата

стороны равны.
Диагонали квадрата равны, взаимно перпендикулярны, делятся в точке

пересечения пополам и являются биссектрисами его углов.


А







d



d

- длина диагонали



  • Имя файла: prezentatsiya-po-teme-cheteryhugolniki-dlya-itogovogo-povtoreniya-v-9-klasse.pptx
  • Количество просмотров: 177
  • Количество скачиваний: 0
- Предыдущая Презентация по изобразительному искусству на тему Жанры в живописи (6 класс)
Следующая - Презентация для учеников начальных классов на тему Прощание со 2 классом

Похожие презентации

Свойство биссектрисы угла треугольника Свойство биссектрисы угла треугольника 171
Презентация по геометрии по теме Инверсия Презентация по геометрии по теме Инверсия 237
Презентация по геометрии на темуТреугольник Презентация по геометрии на темуТреугольник 152
Презентация Решение задач по теме площади геометрия 8 класс Презентация Решение задач по теме площади геометрия 8 класс 176
ШАР. СФЕРА ШАР. СФЕРА 172
Анализ геометрической формы предмета Анализ геометрической формы предмета 172
Симметрия на планете Земля Симметрия на планете Земля 159
Элементы теории графов Элементы теории графов 190
Презентация.Прикладные основы расчета различных типов кредитов Презентация.Прикладные основы расчета различных типов кредитов 220
Геометрия и лист бумаги Геометрия и лист бумаги 141
Презентация по математике на тему Площадь многоугольника (8 класс) Презентация по математике на тему Площадь многоугольника (8 класс) 153
Геометрия в жизни Геометрия в жизни 164
Презентация. Гл. 1. Урок 6. Трапеция. Презентация. Гл. 1. Урок 6. Трапеция. 166
Презентация к уроку геометрии 7 класс на тему Треугольник. Интересные факты о треугольнике Презентация к уроку геометрии 7 класс на тему Треугольник. Интересные факты о треугольнике 231
Координаты на плоскости Координаты на плоскости 166
Сечения многогранников Сечения многогранников 167
Построение сечений параллелепипеда Построение сечений параллелепипеда 162
Сумма углов треугольника Сумма углов треугольника 158
Части фигур Части фигур 141
Перпендикулярность в пространстве Перпендикулярность в пространстве 144
Усечённая пирамида Усечённая пирамида 174
Презентация по геометрии Теорема Пифагора Презентация по геометрии Теорема Пифагора 177
Построение аксонометрических проекций Построение аксонометрических проекций 152
Гл.2. Урок 3. Площадь параллелограмма Гл.2. Урок 3. Площадь параллелограмма 174
Тела вращения Тела вращения 155
Треугольник и многоугольник. Плоскость, прямая и луч Треугольник и многоугольник. Плоскость, прямая и луч 170
Виды углов Виды углов 196
Прямоугольная система координат на плоскости Прямоугольная система координат на плоскости 178
Многоугольники. Решение задач Многоугольники. Решение задач 174
Презентация к уроку геометрии: Решение задач по теме-Векторы (9класс) Презентация к уроку геометрии: Решение задач по теме-Векторы (9класс) 112