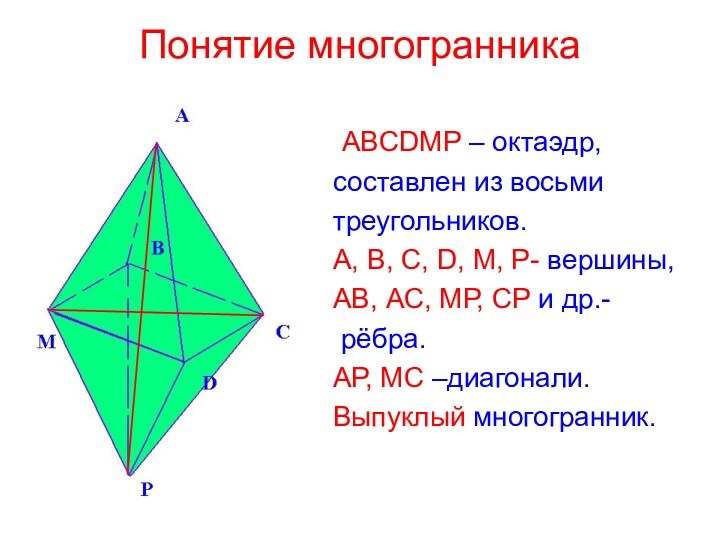
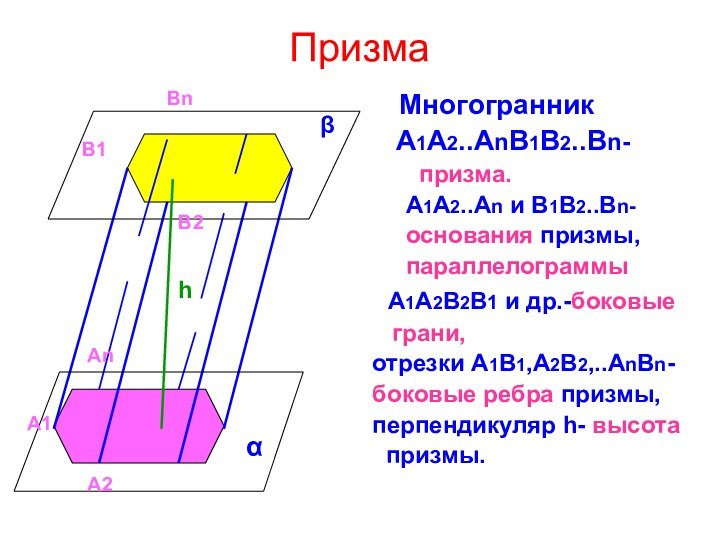
C, D, M, P- вершины,
АВ, АС, МР, СР и
др.-рёбра.
АР, МС –диагонали.
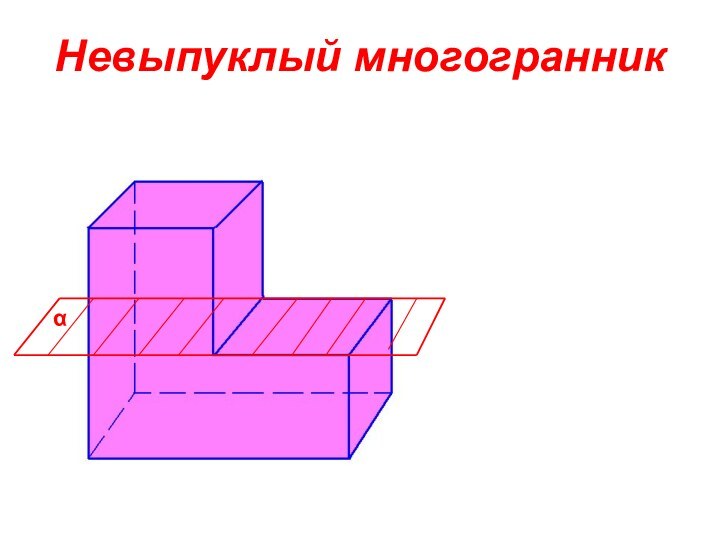
Выпуклый многогранник.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть







А1
А2
Аn
B1
B2
Bn
α
β
h
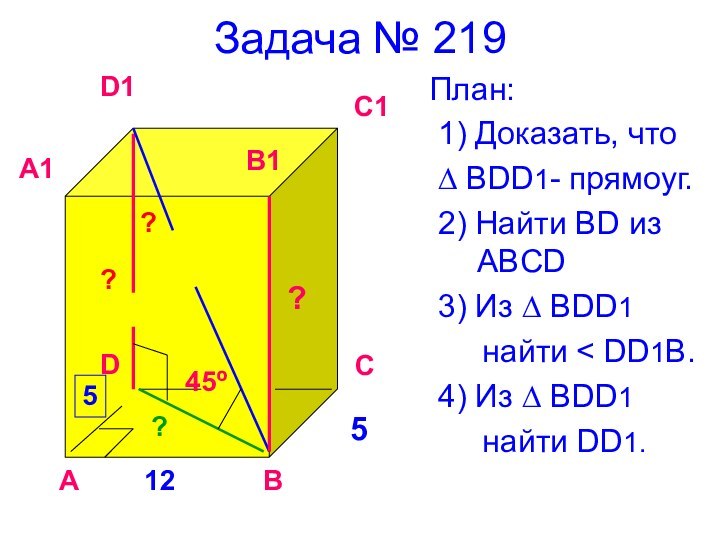
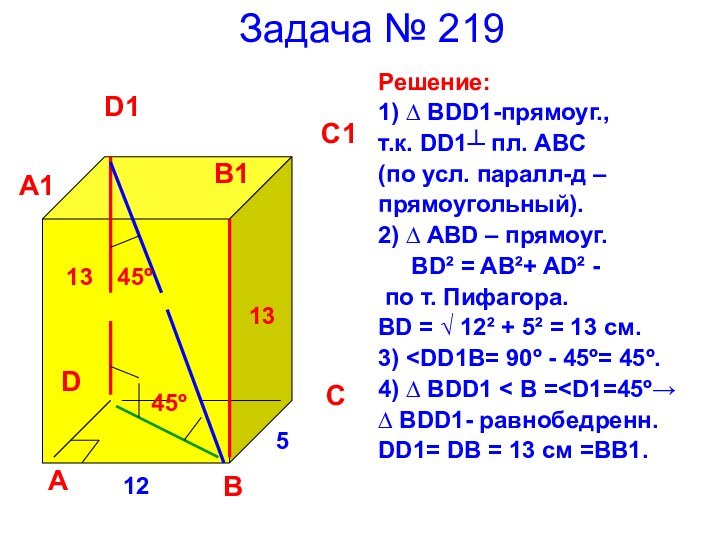
12
5
45º
?
А
В
С
D
A1
D1
C1
B1
5
?
?
?
А
В
С
D
A1
B1
C1
D1
45º
12
5
13
13
45º
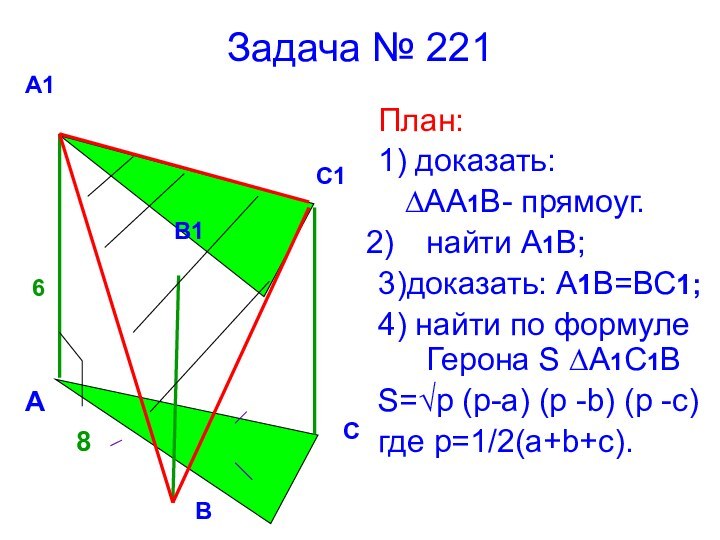
8
6
А
В
С
А1
В1
С1
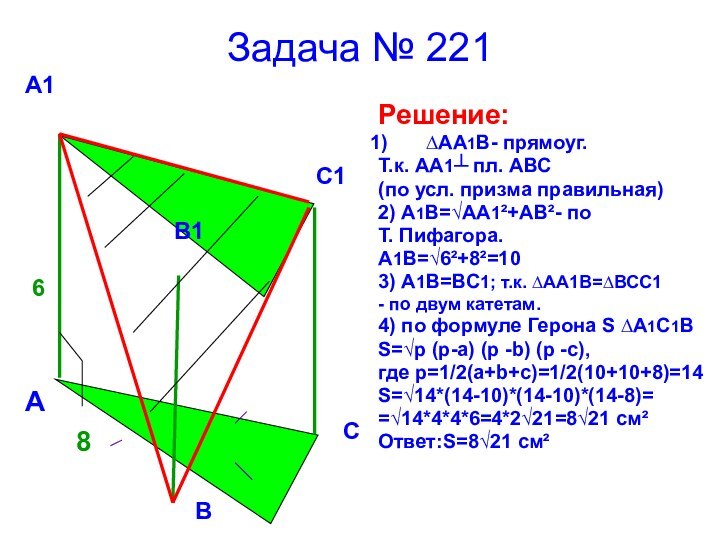
8
6
А
В
С
А1
В1
С1