красотой - красотой отточенной и строгой, возвышенно чистой и
стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.Бертран Рассел
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


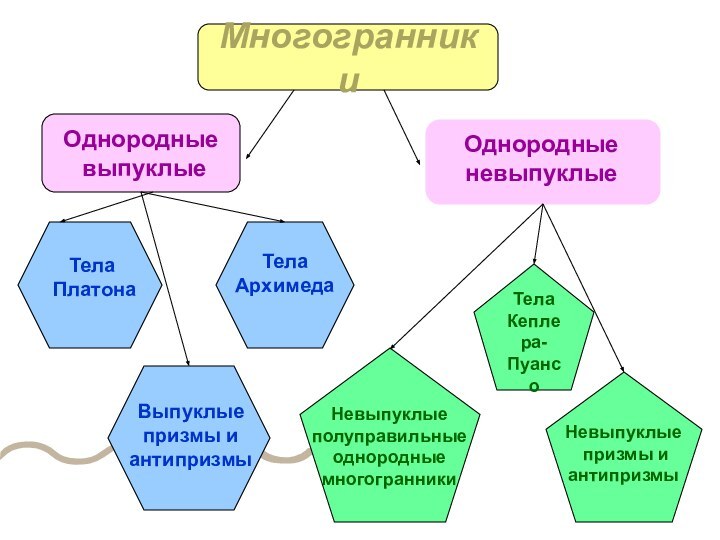


















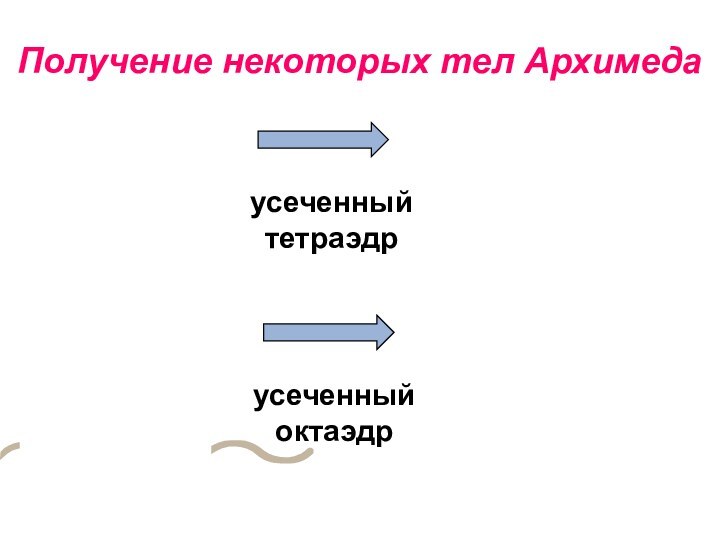









Тела
Архимеда
Тела
Платона
Выпуклые
призмы и
антипризмы
Тела
Кеплера-
Пуансо
Невыпуклые
полуправильные
однородные
многогранники
Невыпуклые
призмы и
антипризмы
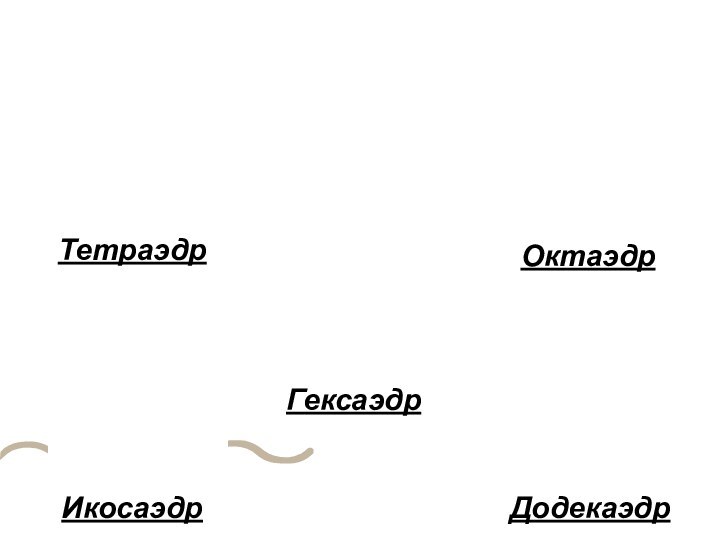
Эти тела еще называют
телами Платона.
На продолжении граней додекаэдра возможны следующие два случая:
если рассматривать правильные пятиугольники, то получается большой додекаэдр;
если же в качестве граней рассматривать звёздчатые пятиугольники, то получается большой звёздчатый додекаэдр.
При продолжении граней правильного икосаэдра получается большой икосаэдр.