Презентация на тему МНОГОГРАННИКИ

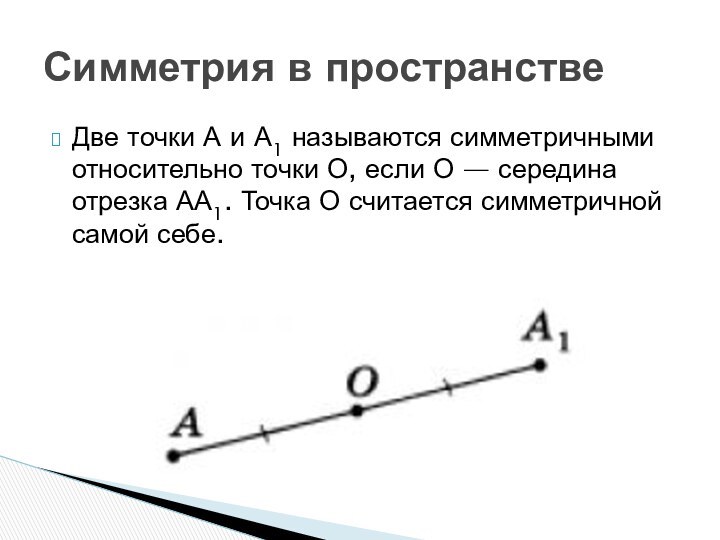
точки О, если О — середина отрезка АА1. Точка

О считается симметричной самой себе.

Симметрия в пространстве

прямой а, если эта прямая проходит через середину отрезка

АА1 и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе.

плоскости α, если плоскость α проходит через середину отрезка

АА1 и перпендикулярна к этому отрезку. Каждая точка плоскости α считается симметричной самой себе.

возможной симметрией
Понятие правильного многогранника

суммы внутренних углов выпуклого n-угольника:
Sn =180°(n – 2), где n

– число сторон, следовательно внутренний угол правильного многоугольника вычисляется по формуле: =
При n6 120°, но при каждой вершине многогранника должно быть не менее трех плоских углов. Поэтому, если бы существовал правильный многогранник, у которого грани – правильные n-угольники при n6, то сумма плоских углов при каждой вершине была бы не меньше 360°, а это невозможно, так как сумма всех плоских углов при каждой вершине выпуклого многогранника меньше 360°.

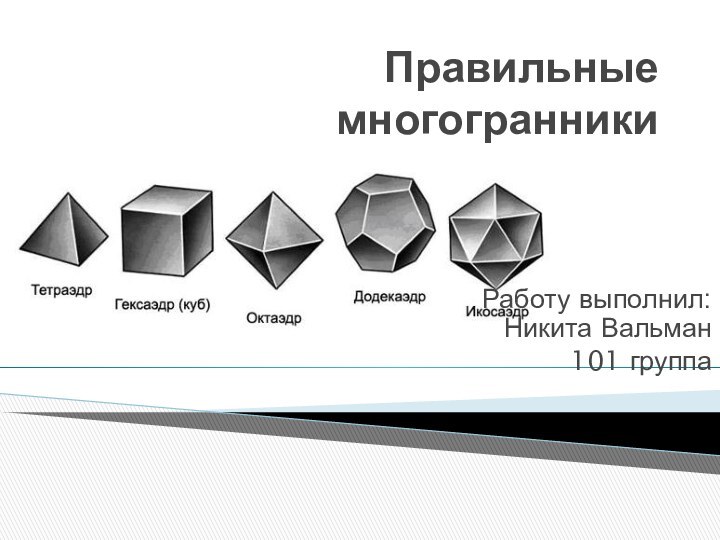
Докажем, что не существует правильного многогранника, гранями которого являются n-угольники при n6.

имеет 3 оси симметрии и шесть плоскостей симметрии.
Куб
У куба

1 центр симметрии - точка пересечения диагоналей куба. Куб имеет 9 плоскостей симметрии.

Элементы симметрии правильных многогранников

симметрии и несколько осей и плоскостей симметрии