три различные точки плоскости можно провести единственную прямую.
2.Если
угол равен 25⁰, то смежный с ним угол равен 155⁰3.Через любую точку плоскости можно провести не менее одной прямой
да
нет
да
нет
да
нет
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть



























































3.Через любую точку плоскости можно провести не менее одной прямой
да
нет
да
нет
да
нет
Через любые две точки проходит прямая , и притом только одна
Сумма смежных углов равна 180°
Через точку на плоскости можно провести бесконечно много прямых.
3.Через любую точку плоскости можно провести не более двух прямых.
да
нет
да
нет
да
нет
3.Если угол равен 47⁰, то смежный с ним угол равен 133⁰.
да
нет
да
нет
да
нет
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Сумма смежных углов равна 180°.
2.Через любые две различные точки плоскости можно провести не менее одной прямой.
3.Если угол равен 54⁰, то вертикальный с ним угол равен 36⁰.
да
нет
да
нет
да
нет
3.Существует точка плоскости, через которую можно провести прямую.
да
нет
да
нет
да
нет
Через любую точку плоскости можно провести прямую.
3.Если при пересечении двух прямых третьей соответственные углы равны, то прямые перпендикулярны.
да
нет
да
нет
да
нет
Сформулируйте свойство параллельных прямых относительно внутренних односторонних углов.
Если две параллельные прямые пересечены третьей прямой, то сума внутренних односторонних углов равна 180°
2.Если при пересечении двух прямых третьей соответственные углы равны 75⁰ и 105⁰, то прямые параллельны
3.Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180⁰, то прямые параллельны
да
нет
да
нет
да
нет
Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны.
Если при пересечении двух прямых третьей соответственные углы равны, то прямые параллельны.
Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180°, то прямые параллельны.
2.Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180⁰, то прямые перпендикулярны.
3.Если две перпендикулярные прямые пересечены прямой, то внутренние накрест лежащие углы равны.
да
нет
да
нет
да
нет
Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны.
Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180°, то прямые параллельны.
2.Если при пересечении двух прямых третьей сумма соответственных углов равна 180⁰, то прямые параллельны.
3.Если две прямые перпендикулярны третьей прямой, то прямые параллельны.
да
нет
да
нет
да
нет
Сформулируйте признак параллельности двух прямых относительно внутренних односторонних углов.
Если прямая перпендикулярна к одной из двух параллельных прямых, то она перепендикулярна и к другой.
Если при пересечении двух прямых третьей соответственные углы равны, то прямые параллельны.
Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180°, то прямые параллельны.
2.Если при пересечении двух прямых третьей внутренние односторонние углы равны 70⁰, то прямые параллельны.
3.Если при пересечении двух прямых третьей внутренние накрест лежащие углы равны 39⁰ и 141⁰, то прямые параллельны.
да
нет
да
нет
да
нет
Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны.
Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180°, то прямые параллельны.
2.Если один из острых углов прямоугольного треугольника равен 25⁰, то другой угол равен 65⁰.
3.Если гипотенуза и катет одного прямоугольного тр-ка соответственно равны гипотенузе и катету другого прямоугольного тр-ка, то тр-ки равны
да
нет
да
нет
да
нет
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Сумма острых углов прямоугольного треугольника равна 90⁰.
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то треугольники равны
2.Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники равны
3.Если один из острых углов прямоугольного треугольника равен 20⁰, то дугой угол равен 80⁰.
да
нет
да
нет
да
нет
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
По двум сторонам и углу между ними, по стороне и прилежащим к ней углам, по трем сторонам.
Сумма острых углов прямоугольного треугольника равна 90⁰.
2.Внешний угол треугольника равен сумме внутренних углов, не смежных с ним.
3.Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
да
нет
да
нет
да
нет
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
да
нет
да
нет
да
нет
Сумма углов треугольника равна 180⁰.
Прямоугольные треугольники могут быть подобными, если выполняется один из признаков подобия треугольников.
Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
2.Если три стороны одного треугольника соответственно в 5 раз больше трех сторон другого треугольника, то такие треугольники подобны.
3.Сумма углов прямоугольного треугольника равна 180⁰.
да
нет
да
нет
да
нет
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны.
Сумма углов треугольника равна 180⁰?
3.В треугольнике против меньшей стороны лежит меньший угол.
да
нет
да
нет
да
нет
Квадрат любой стороны треугольника равен сумме квадратов других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
2.В треугольнике АВС, для которого ∠А=40⁰, ∠В=55⁰, ∠85⁰, сторона АС – наименьшая.
3.Каждая сторона треугольника меньше суммы других сторон.
да
нет
да
нет
да
нет
Сформулируйте теорему о соотношениях между сторонами и углами треугольника.
В треугольнике против большей стороны лежит больший угол, и наоборот, против большего угла лежит большая сторона.
Каждая сторона треугольника меньше суммы двух других сторон.
2.В любой прямоугольный треугольник можно вписать окружность.
3.Центр окружности, описанного около прямоугольного треугольника, находится на катете этого треугольника.
да
нет
да
нет
да
нет
В какой треугольник можно вписать окружность?
Где лежит центр окружности, описанной около прямоугольного треугольника?
Центры таких окружностей совпадают и лежат в точке пересечения серединных перпендикуляров к сторонам треугольника.
В любой треугольник можно вписать окружность, а значит и прямоугольный?
Центр окружности, описанной около прямоугольного треугольника лежит в середине гипотенузы прямоугольного треугольника.
3.Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров, проведенных у его сторонам.
да
нет
да
нет
да
нет
Сформулируйте теорему о соотношениях между сторонами и углами треугольника.
В треугольнике против большей стороны лежит больший угол, и наоборот, против большего угла лежит большая сторона.
3.Кажддая сторона треугольника больше суммы двух других сторон.
да
нет
да
нет
да
нет
В какой точке лежит центр окружности, описанной около треугольника?
Центр окружности, описанной около треугольника лежит в точке пересечения серединных перпендикуляров к сторонам треугольника.
Сформулируйте неравенство треугольника.
Каждая сторона треугольника меньше суммы двух других сторон.
3.В любой четырехугольник можно вписать окружность.
да
нет
да
нет
да
нет
Если диагональ четырехугольника перпендикулярны и делят углы четырехугольника пополам, то этот четырехугольник – ромб.
В четырехугольник можно вписать окружность, если суммы противоположных углов равны 180⁰
3.Около любого четырехугольника можно описать окружность.
да
нет
да
нет
да
нет
3.Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм – ромб.
да
нет
да
нет
да
нет
Около какой четырехугольника можно описать окружность?
Около четырехугольника можно описать окружность, если суммы противоположных сторон четырехугольника равны .
Суммы противоположных углов вписанного в окружность четырехугольника равны 180⁰
Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм – ромб.
3.Диагонали прямоугольника равны.
да
нет
да
нет
да
нет
В четырехугольник, суммы противоположных сторон которого равны, можно вписать окружность.
Диагонали прямоугольника равны.
да
нет
да
нет
да
нет
3.Длина окружности радиуса R равна πR.
да
нет
да
нет
да
нет
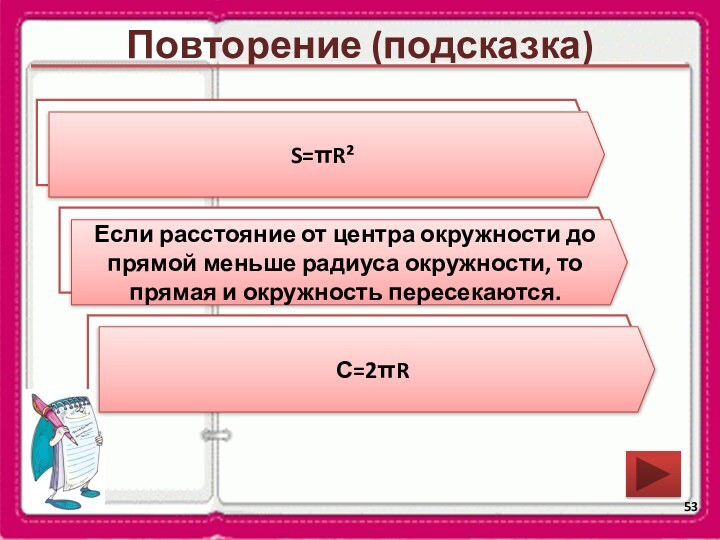
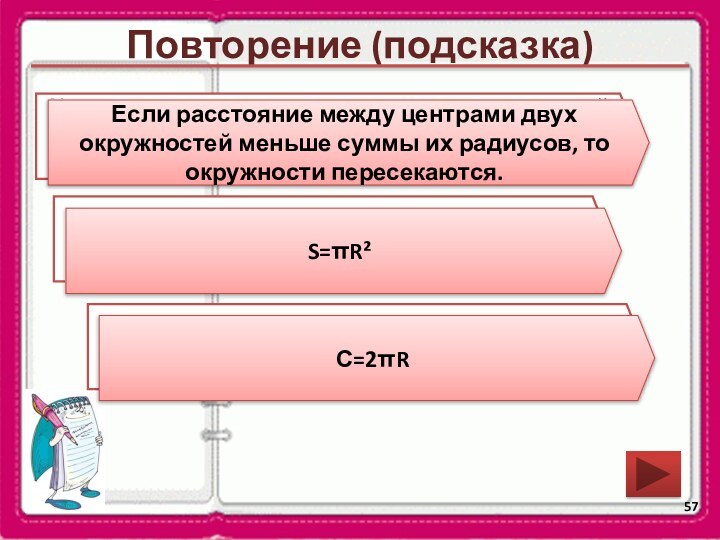
S=πR²
Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность пересекаются.
С=2πR
2.Если радиус окружности равна 3, а расстояние от центра окружности до прямой равно 2, эти прямая и окружность не имеют общих точек.
3.Через любые три различные точки плоскости, не лежащие на одной прямой, можно провести не более одной окружности
да
нет
да
нет
да
нет
Если расстояние между центрами двух окружностей больше суммы их радиусов, то окружности не пересекаются.
При каком условии прямая и окружность не пересекаются?
Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не пересекаются.
Через три точки плоскости можно провести окружность, если центр окружности лежит на биссектрисе угла, вершина которого лежит в одной из данных точек, стороны этого угла проходят через две другие точки, и центр окружности равноудален от данных точек.
Значит такая окружность единственная.
2.Площадь круга радиуса R равна 2πR.
3.Длина окружности радиуса R равна 2πR.
да
нет
да
нет
да
нет
По какой формуле можно вычислить площадь круга?
S=πR²
По какой формуле можно вычислить длину окружности?
С=2πR
да
нет
да
нет
да
нет
S=πR²
Градусная мера вписанного угла равна половине дуги, на которую он опирается.
Градусная мера центрального угла равна дуге, на которую он опирается.
2.Если расстояние между центрами двух окружностей больше суммы их радиусов, то эти окружности пересекаются.
3.Если расстояние от центра окружности до прямой меньше диаметра окружности, то эти прямая и окружность пересекаются.
да
нет
да
нет
да
нет
При каком условии прямая и окружность пересекаются?
Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность пересекаются.
Каково взаимное положение двух окружностей, если расстояние между их центрами больше суммы их радиусов?
Если расстояние между центрами двух окружностей больше суммы их радиусов, то окружности не пересекаются.