Презентация на тему Симметрия в окружающем мире

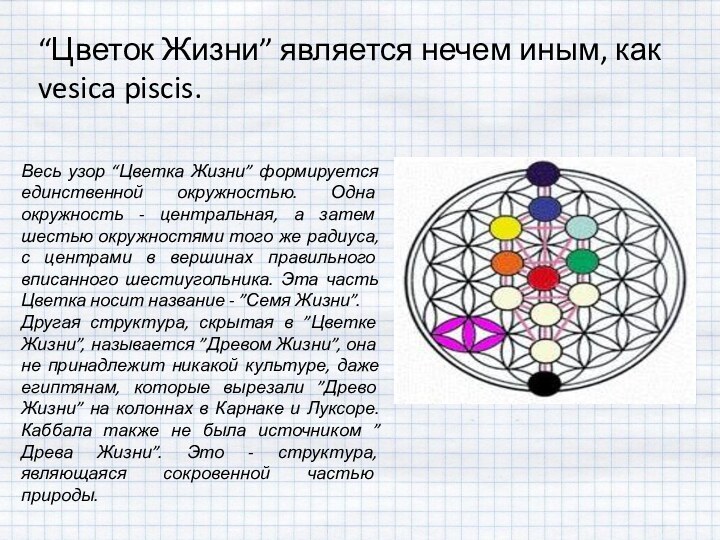
Скалярная геометрия «Цветок Жизни»
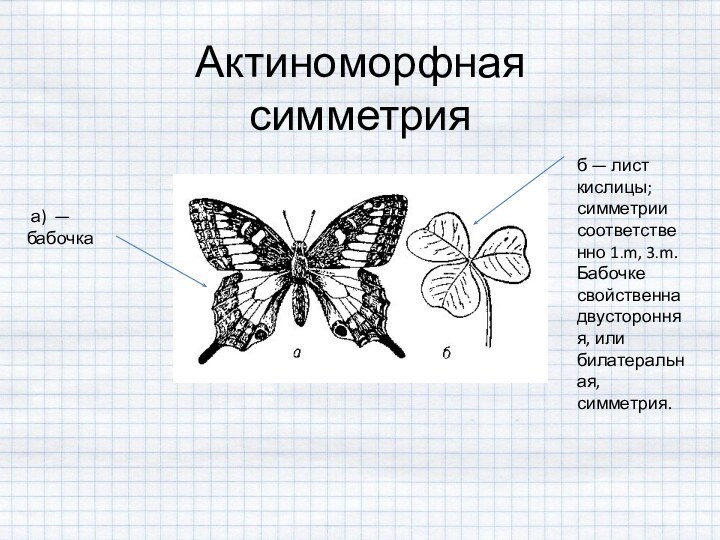
4. Симметрия у цветков и растений
5.

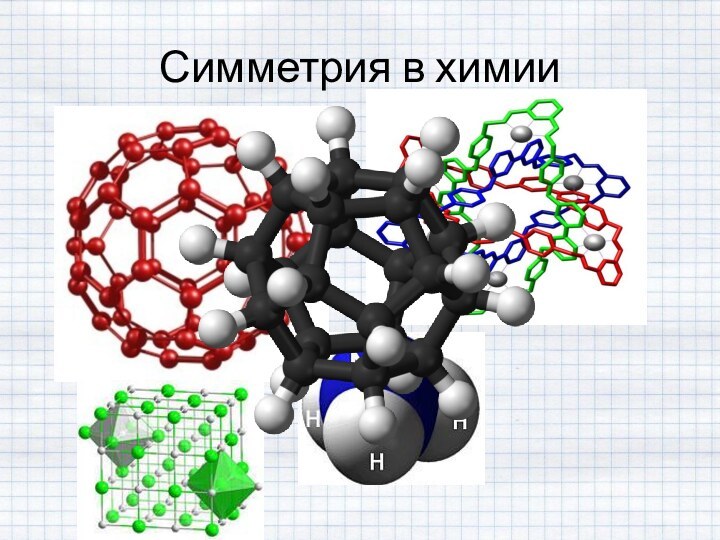
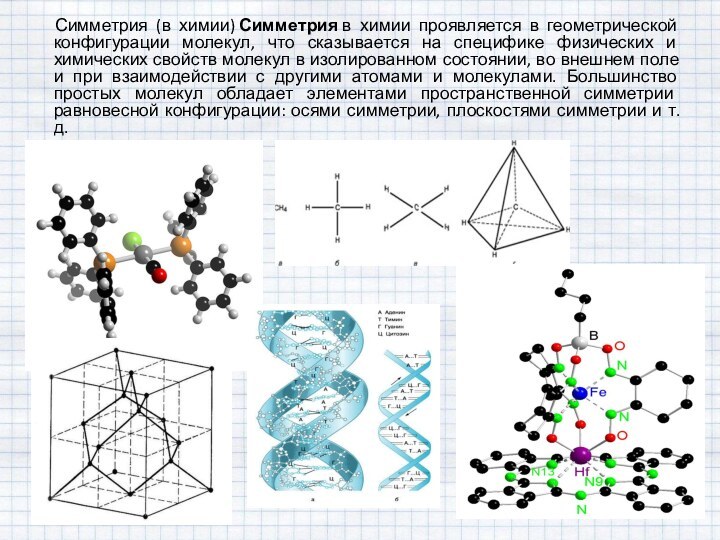
Радиальная симметрия
6. Симметрия в химии
7.Симметрия вокруг нас

в гипотезах и теориях учёных прошлых веков, веривших в

математическую гармонию мироздания и видевших в этой гармонии проявление божественного начала. Древние греки считали, что Вселенная симметрична просто потому, что симметрия прекрасна. В своих размышлениях над картиной мироздания человек с давних времен активно использовал идею симметрии.

что симметрия прекрасна. Исходя из соображений симметрии, они высказали

ряд догадок.

симметричной и совершенной формой, делал вывод о сферичности Земли

и о ее движении по сфере. При этом он полагал, что Земля движется по сфере некоего «центрального огня». Вокруг того же «огня», согласно Пифагору, должны были обращаться известные в те времена шесть планет, а также Луна, Солнце, звезды

понятиями теории симметрии.
Такие, которые совершенно одинаковы, или, точнее, которые при

взаимном наложении совмещаются друг с другом во всех своих деталях, как, например, два лепестка на рисунке 1.

Пары лепестков:
а — совместимо равные;
б — зеркально равные;
в — и совместимо и зеркально равные. Фигуры из пяти лепестков:
г — расположенных относительно друг друга хаотично;
д — закономерно. Верхняя фигура асимметричная, нижняя — симметричная.

лишь для объектов, вытянутых в одном особенном направлении АВ. Наименьший путь а, который

должен быть пройден рядом фигур, прежде чем произойдет самосовмещение, называется элементарным переносом. Операции переноса также соответствует особый элемент симметрии — ось переносов (а):прямая АВ или любая прямая, параллельная АВ. Ось переносов (о) присуща только бесконечным фигурам, тем, которые бесконечно вытянуты лишь в одном особенном направлении (типа «стержней»), в двух особенных направлениях (типа «слоев»), в трех особенных направлениях (типа «кристаллов»). При этом считается, что телам, не вытянутым бесконечно ни в одном особенном направлении (типа изображенных на рисунках 2, 3, 4, 5), присуща нульмерная симметрия; телам, вытянутым в одном особенном направлении, — одномерная симметрия, в двух — двумерная симметрия, в трех — трехмерная симметрия. А теперь каждую из этих симметрии рассмотрим по порядок.

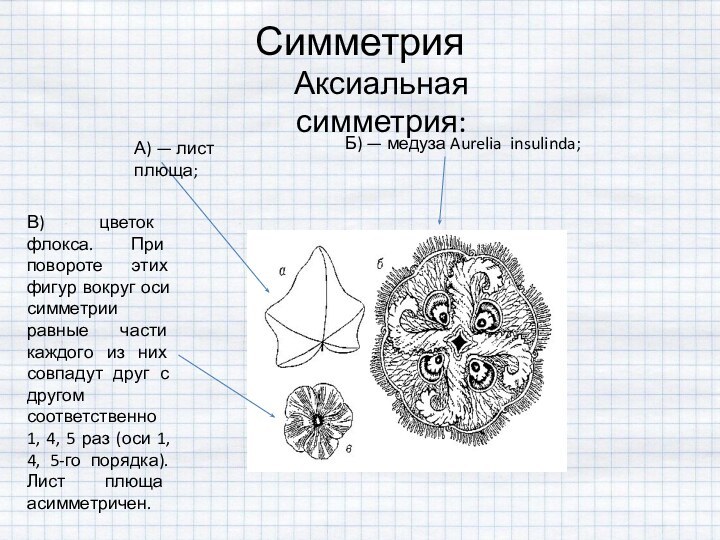
Аксиальная симметрия:
а — медуза аурелия инсулинда;
б — детская вертушка;
в — молекула химического соединения. При повороте этих фигур на 360о равные части фигур совпадут друг с другом соответственно 4, 4, 6 раз.

единственное изображение, которое содержит в себе до единого аспекты

творения, все математические формулы, каждый закон физики, каждую гармонию в музыке и каждую биологическую жизнеформу. Сакральная геометрия имеет одну особенность — она безупречна, всё в мире связано с ней, она основа творения, в геометрии “Цветка Жизни” заключен образ творения. Всё, что существует в мире или было когда-либо сотворено, создавалось по этому образцу и имеет в своей основе сакральную геометрию.

узор “Цветка Жизни” формируется единственной окружностью. Одна окружность -

центральная, а затем шестью окружностями того же радиуса, с центрами в вершинах правильного вписанного шестиугольника. Эта часть Цветка носит название - ”Семя Жизни”.
Другая структура, скрытая в ”Цветке Жизни”, называется ”Древом Жизни”, она не принадлежит никакой культуре, даже египтянам, которые вырезали ”Древо Жизни” на колоннах в Карнаке и Луксоре. Каббала также не была источником ”Древа Жизни”. Это - структура, являющаяся сокровенной частью природы.

гранью квадрат, и все его грани - одинакового размера),

все рёбра  имеют одинаковую длину (все рёбра куба – одной длины), все внутренние углы между гранями имеют одинаковую величину (в случае куба, этот угол равен 90 градусам), и четвёртое, если Платоново тело поместить внутрь сферы (правильной формы), то все вершины его будут касаться поверхности сферы. 

медуза Aurelia insulinda;
В) цветок флокса. При повороте этих

фигур вокруг оси симметрии равные части каждого из них совпадут друг с другом соответственно 1, 4, 5 раз (оси 1, 4, 5-го порядка). Лист плюща асимметричен.

Бабочке свойственна двусторонняя, или билатеральная, симметрия.
Актиноморфная симметрия
 а) —

бабочка

— додекаэдра и икосаэдра.
Биообъекты с совершенной точечной симметрией. Радиолярии
А)-

шарообразная Ethmosphaera polysyphonia, содержащая бесконечное число осей бесконечного порядка + бесконечное число плоскостей симметрии + центр симметрии

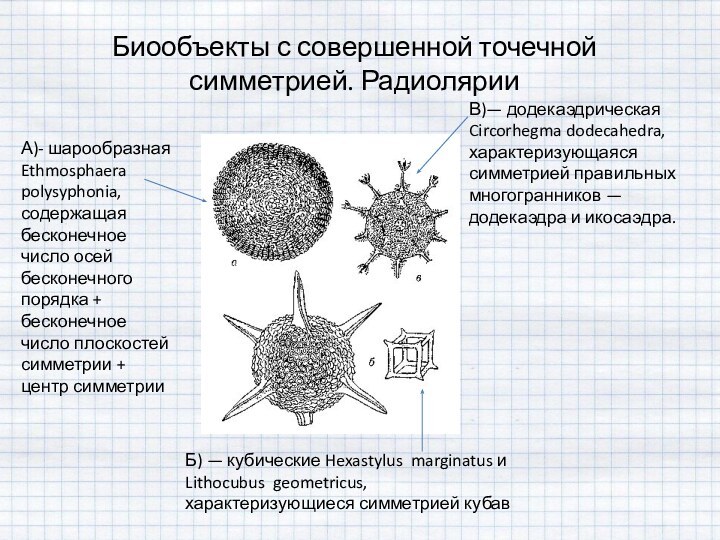
Б) — кубические Hexastylus marginatus и Lithocubus geometricus, характеризующиеся симметрией кубав

другом путем вращения вокруг точки S. Эта точка называется

центром симметрии.

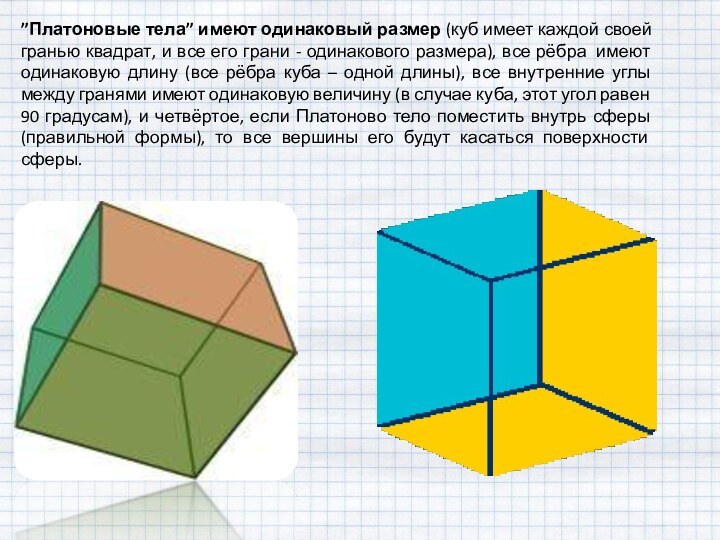
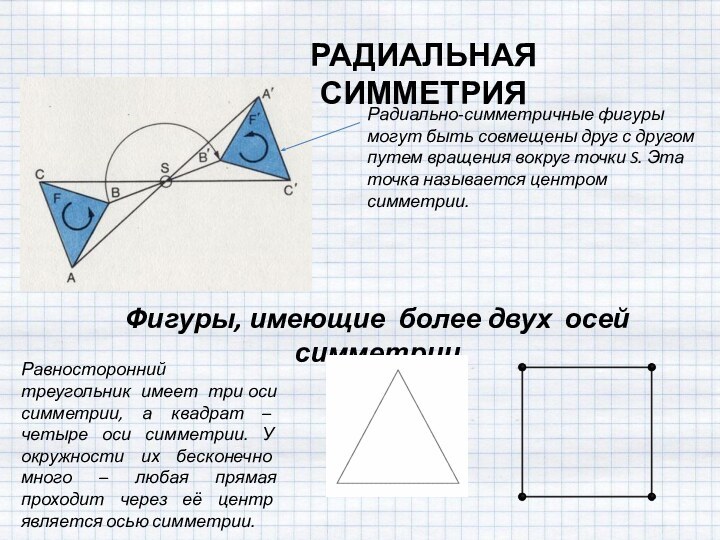
Фигуры, имеющие более двух осей симметрии

Равносторонний треугольник имеет три оси симметрии, а квадрат – четыре оси симметрии. У окружности их бесконечно много – любая прямая проходит через её центр является осью симметрии.

молекул, что сказывается на специфике физических и химических свойств

молекул в изолированном состоянии, во внешнем поле и при взаимодействии с другими атомами и молекулами. Большинство простых молекул обладает элементами пространственной симметрии равновесной конфигурации: осями симметрии, плоскостями симметрии и т. д.