Презентация на тему по геометрии на тему Векторы (10 класс)

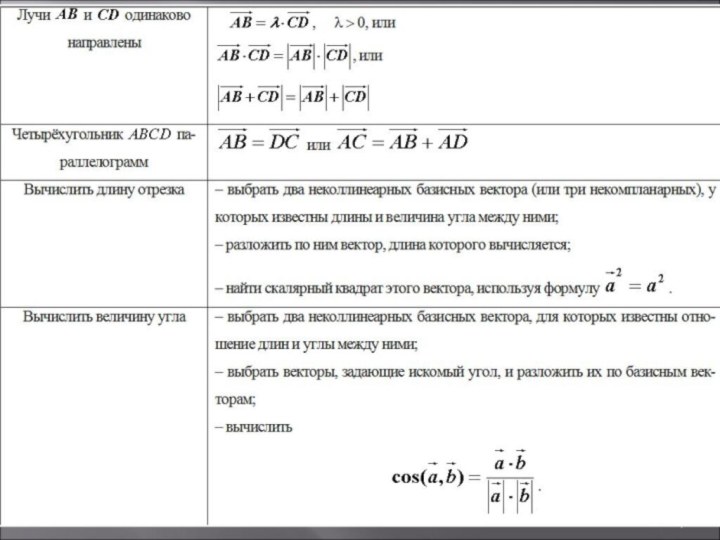
решения задач и доказательства теорем, при котором геометрические отношения

формулируются в векторно-координатных терминах, и дальнейшие рассуждения проводятся с использованием векторно-координатных понятий и их свойств.
Для решения задач элементарной геометрии с помощью векторов необходимо, прежде всего, научиться «переводить» условие геометрической задачи на «векторный» язык. После такого перевода осуществляются алгебраические вычисления с векторами, а затем полученное снова «переводится» на «геометрический» язык. В этом и состоит сущность векторного метода решения геометрических задач.

базисных вектора, для которых известны отношение длин и углы

между ними;
– выбрать векторы, задающие искомый угол, и разложить их по базисным векторам;
– вычислить (искомый угол должен быть острым).
2 способ.
– определить координатные оси;
– найти координаты векторов, задающие искомый угол;
– вычислить (искомый угол должен быть острым).

ABCDA1B1C1D1 найдите косинус угла между прямыми AB и CA1.
1.

Определим систему координат и координаты точек A, B, C, A1 в этой системе координат:

A (0; 0; 0); B (a; 0; 0); C (a; a; 0); A1 (0; 0; a).

2. Найдем координаты векторов

Ответ:

выбрать три некомпланарных базисных вектора, для которых известны отношение

длин и углы между ними;
– выбрать вектор, параллельный данной прямой;
– разложить выбранный вектор и вектор нормали к данной плоскости по базисным векторам;
– вычислить
– искомый угол равен
2 способ.
– определить координатные оси;
– найти координаты вектора, параллельного данной прямой и вектора нормали к плоскости;
– вычислить
– искомый угол равен

1
A(0; 0; 0); B(1; 0; 0); B1(1; 0; 1);

C1(0,5; ; 1).

В правильной треугольной призме ABCA1B1C1 все ребра которой равны 1, найдите тангенс угла между прямой BB1 и плоскостью AB1C1.

1. Определим систему координат и координаты точек A, B, B1, C1 в этой системе координат:

2. Найдем координаты вектора

1
В правильной треугольной призме ABCA1B1C1 все ребра которой равны

1, найдите тангенс угла между прямой BB1 и плоскостью AB1C1.

3. Определим уравнение плоскости AB1C1.

Уравнение плоскости AB1C1:

Вектор нормали к плоскости

1
В правильной треугольной призме ABCA1B1C1 все ребра которой равны

1, найдите тангенс угла между прямой BB1 и плоскостью AB1C1.

Ответ:

написать уравнения плоскостей, угол между которыми требуется определить;
– найти

координаты векторов нормали к данным плоскостям;
– вычислить угол между векторами нормали

ABCDA1B1C1D1 найдите косинус угла между плоскостями BA1C1 и AB1D1.

1. Определим систему координат и координаты точек B, A1, C1, A, B1, D1 в этой системе координат:

A (0; 0; 0); B (a; 0; 0); A1 (0; 0; a); C1 (a; a; a); B1 (a; 0; a); D1 (0; a; a).

2. Составим уравнения плоскостей
Плоскость BA1C1:

Вектор нормали

ABCDA1B1C1D1 найдите косинус угла между плоскостями BA1C1 и AB1D1.

A (0; 0; 0); B (a; 0; 0); A1 (0; 0; a); C1 (a; a; a); B1 (a; 0; a); D1 (0; a; a).

Плоскость AB1D1:

Вектор нормали

Вектор нормали

Ответ:

правильной четырёхугольной призме ABCDA1B1C1D1, стороны основания равны 1, а

боковые рёбра равны 3. На ребре AA1 отмечена точка E так, что . Найдите угол между плоскостями ABC и BED1.

1.

AE = 2, EA1=1.

2. Введем систему координат: A (0; 0; 0); B (1; 0; 0); D (0; 1; 0); A1 (0; 0; 3); E (0; 0; 2); D1 (0; 1; 3).

3. Составим уравнение плоскости BED1:

Уравнение плоскости BED1:

Вектор нормали к плоскости BED1: