Презентация на тему Объёмы геометрических тел

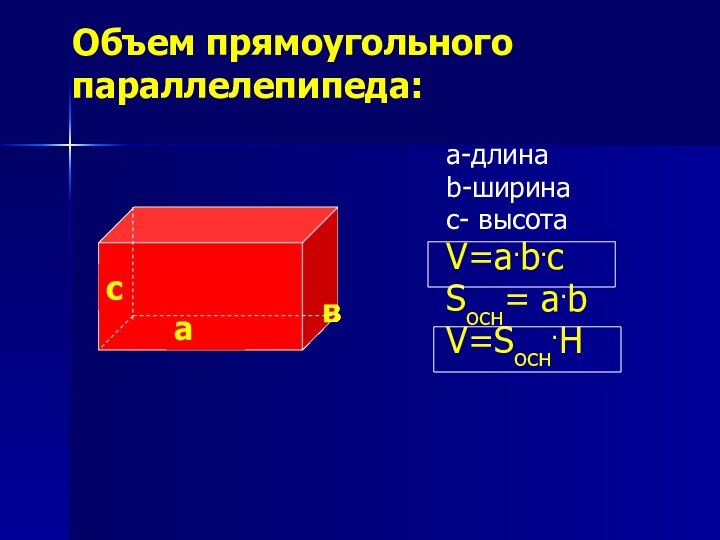
измерения объёма.
Повторить с учащимися формулы для нахождения объёма

параллелепипеда, куба.
Познакомить учащихся с объёмами прямой призмы, пирамиды, цилиндра и конуса, руководствуясь наглядно-иллюстративными соображениями.

науки стремятся к математике.

Д. Сантаяна

Пойа Д.

Площадь многоугольника- это положительная величина той части плоскости ,

которую занимает многоугольник.

Объем

Объем тела – это положительная величина той части пространства , которую занимает геометрическое тело.

Равные тела имеют равные объемы



F1
F2

F1

F2

то его площадь равна сумме площадей этих многоугольников.

SF=SF1+SF2+SF3+SF4

2. Если тело составлено из нескольких тел , то его объем равен сумме объемов этих тел.







VF=VF1+VF2

измерения площадей берут квадрат, сторона которого равна единице измерения

отрезков.
1 км2, 1 м2, 1 дм2, 1 см2, 1 мм2 , 1 а, 1 га и т.д.

Объем
За единицу измерения объемов примем куб, ребро которого равно единице измерения отрезков.
Куб с ребром 1 см называют кубическим сантиметром и обозначают см3.
Аналогично определяют
1 м3, 1 дм3, 1 см3 , 1 мм3 и т.д.

1

1

1

1

1

площади

Объем
Равновеликими называются тела, объемы которых

равны

VF=VF1

F2

F1

F2

F1

SF=SF1

и объемы тел вращения.

призмы = (V парал) :2
V призмы = (2.SABС. H):

2

общая,
тр CC1B1= тр CBB1
У 1 и 3 пирамиды-

СS- общая,
тр SAB= тр BB1S
V1=V2=V3
V призмы= 3 V пирам
Vпирамиды=1 V призмы
3
Vпирамиды=1 Sосн .H
3

Достроим пирамиду
ABCS до призмы. Достроенная
призма будет состоять из 3
пирамид- SABC, SCC1B1, SCBB1

H - высота
L - образующая
L=H

V - объем цилиндра

V = ПR2H - объём
V= Sосн .H
Sосн= ПR2

ОБОЗНАЧЕНИЯ:
R - радиус основания

L - образующая конуса H – высота
V – объем


V=1ПR2Н
3 - объём

тел.
Назовите единицы измерения объема тел.
Назовите формулу для измерения объема

- прямоугольного параллелепипеда;
- объема куба;
- объем прямой призмы;
- объем пирамиды;
- объем цилиндра и объем конуса.
Изменится ли объем цилиндра, если радиус его основания увеличить в 2 раза, а высоту уменьшить в 4 раза?
V = ПR2H V=П(2R)2 .H =П4R2. H =ПR2. H
4 4
Основаниями двух пирамид с равными высотами являются четырехугольники с соответственно равными сторонами. Равны ли объемы этих пирамид?
Из каких тел состоит тело, полученное вращением равнобедренной трапеции вокруг большего основания?

№ 685, № 666(а,в)

куба с ребрами 3см, 4 см и 5 см

переплавлены в один куб. Какое ребро у этого куба?

+ + =

+125=216 (см3)
VF=а3
а3=216 (см3)
а= 6 (см)
Ответ: ребро куба равно 6

см.

пирамиды, высота которой равна 12 см, а сторона основания

13 см.

квадрат
S ABCD=a2
S ABCD= 132=169
V=1 169 . 12

=676 (см3)
3
Ответ : Объем правильной четырехугольной пирамиды равен 676 см3

его основания равен 6см, а высота 8 см.

=288П (см3)

Ответ: объем цилиндра равен 288 П см3 .

Варенко Оксаной Валентиновной в программах: Microsoft Office Word, Paint.
В

данной работе использованы фотографиии c сайтов
- - ru.wikipedia.org- ru.wikipedia.org›wiki/Конус_выноса
images.yandex.ru›конус нарастания
medusy.rumedusy.ru›diving/yad_mollusk/index.shtm
reinesland.rureinesland.ru›wiki/Телесный_угол