- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
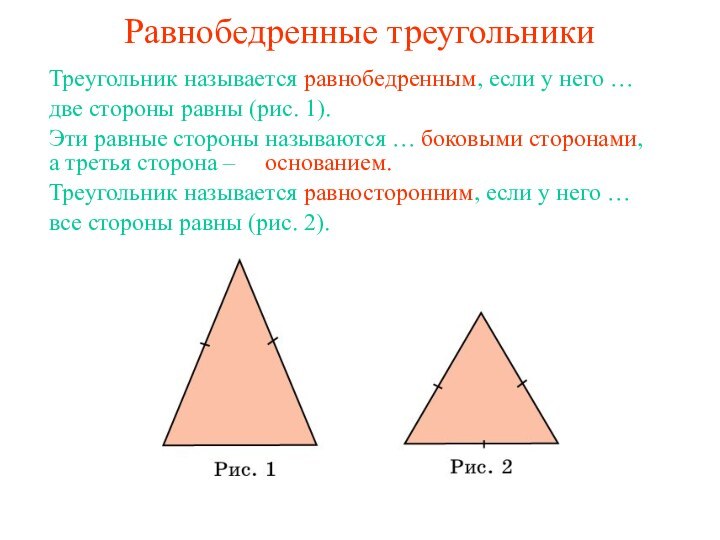
Презентация на тему Равнобедренные треугольники
Содержание
- 2. ТеоремаВ равнобедренном треугольнике биссектриса, проведенная к основанию, является одновременно медианой и высотой.
- 3. Упражнение 1На рисунке AB = BC. Докажите, что 1 = 2.
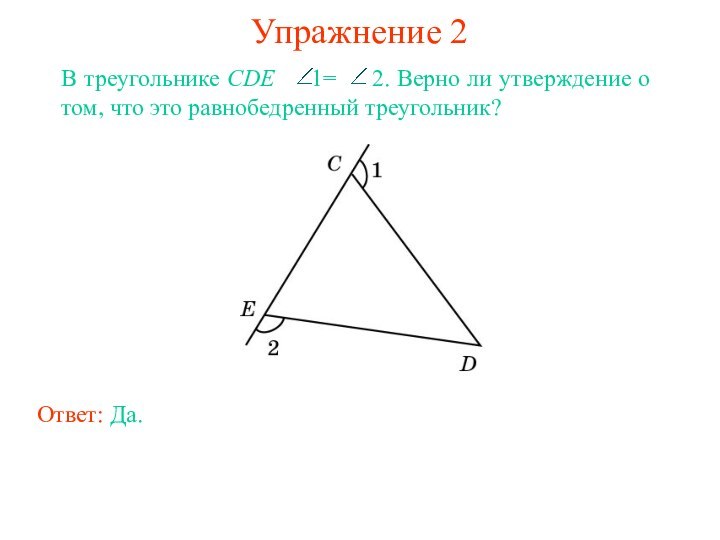
- 4. Упражнение 2Ответ: Да.
- 5. Упражнение 3Ответ: а), б), в) Да.
- 6. Упражнение 4Ответ: 0,8 м.Периметр равнобедренного треугольника равен
- 7. Упражнение 5Ответ: 3,5 м.Периметр равнобедренного треугольника равен
- 8. Упражнение 6Ответ: а) 3,2 м; 6, 2
- 9. Упражнение 7Ответ: 6 см; 16 см; 16
- 10. Упражнение 8Ответ: 15 м.В равнобедренном треугольнике АВС
- 11. Упражнение 9Доказательство: Пусть треугольник ABC равнобедренный (AC
- 12. Упражнение 10
- 13. Упражнение 11
- 14. Упражнение 12Доказательство: Пусть ABC – равнобедренный треугольник
- 15. Упражнение 13
- 16. Упражнение 14Доказательство: Треугольники ADF и BED равны
- 17. Скачать презентацию
- 18. Похожие презентации
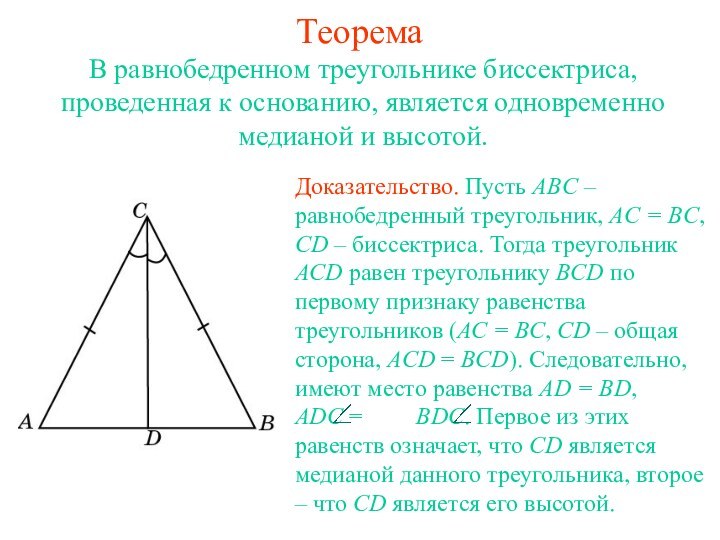
ТеоремаВ равнобедренном треугольнике биссектриса, проведенная к основанию, является одновременно медианой и высотой.













Слайд 2
Теорема
В равнобедренном треугольнике биссектриса, проведенная к основанию, является
одновременно медианой и высотой.
Слайд 6
Упражнение 4
Ответ: 0,8 м.
Периметр равнобедренного треугольника равен 2
м, а основание - 0,4 м. Найдите боковую сторону.
Слайд 7
Упражнение 5
Ответ: 3,5 м.
Периметр равнобедренного треугольника равен 7,5
м, а боковая сторона - 2 м. Найдите основание.
Слайд 8
Упражнение 6
Ответ: а) 3,2 м; 6, 2 м;
6,2 м;
Периметр равнобедренного треугольника равен 15,6 м. Найдите
его стороны, если: а) основание меньше боковой стороны на 3 м; б) основание больше боковой стороны на 3 м.б) 7,2 м; 4,2 м; 4,2 м.
Слайд 9
Упражнение 7
Ответ: 6 см; 16 см; 16 см.
Основание и боковая сторона равнобедренного треугольника относятся как 3:8.
Найдите стороны этого треугольника, если его периметр равен 38 см.
Слайд 10
Упражнение 8
Ответ: 15 м.
В равнобедренном треугольнике АВС с
основанием АС проведена медиана BD. Найдите ее длину, если
периметр треугольника АВС равен 50 м, а треугольника АВD - 40 м.
Слайд 11
Упражнение 9
Доказательство: Пусть треугольник ABC равнобедренный (AC =
BC). N, M, K – середины сторон. Тогда треугольники
AMN и BMK равны по первому признаку и, следовательно, NM = MK, т.е. треугольник NMK равнобедренный.Докажите, что середины сторон равнобедренного треугольника являются вершинами также равнобедренного треугольника.
Слайд 14
Упражнение 12
Доказательство: Пусть ABC – равнобедренный треугольник (AB
= BC), AN и CM – медианы. Тогда AM
= CN и треугольники ACM и CAN равны по первому признаку. Следовательно, AN = CM.По рисунку докажите, что медианы равнобедренного треугольника, проведенные к его боковым сторонам, равны.
Слайд 16
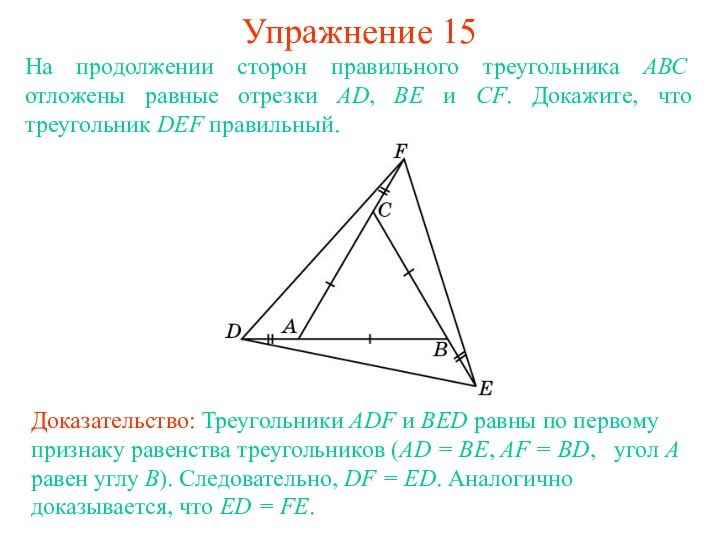
Упражнение 14
Доказательство: Треугольники ADF и BED равны по
первому признаку равенства треугольников (AD = BE, AF =
BD, угол A равен углу B). Следовательно, DF = ED. Аналогично доказывается, что ED = FE.На сторонах правильного треугольника АВС отложены равные отрезки AD, BE и CF. Точки D, E и F соединены отрезками. Докажите, что треугольник DEF правильный.





























