- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Пирамида
Содержание
- 2. ПланОпределениеЭлементы пирамидыСвойства пирамидыПравильная пирамидаСвойства правильной пирамидыПрямоугольная пирамидаПоверхность пирамидыФормулы, связанные с пирамидой
- 3. ОпределениеПирамида – это многоугольник А1А2…Аn и точка
- 4. Элементы пирамидыоснование — многоугольник, которому не принадлежит
- 5. Свойства пирамидыЕсли боковые грани наклонены к плоскости
- 6. Свойства пирамидыЕсли все боковые ребра равны, то:около
- 7. Свойства пирамидыЕсли в основании пирамиды лежит прямоугольный
- 8. Правильная пирамидаПирамида называется правильной, если ее основанием является правильный многоугольник, а вершина проецируется в центр основания.
- 9. Свойства правильной пирамидыбоковые ребра правильной пирамиды равны;в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
- 10. Прямоугольная пирамидаПирамида называется прямоугольной, если одно из
- 11. Поверхность пирамидыПлощадью полной поверхности пирамиды называется сумма
- 12. Формулы, связанные с пирамидойЧтобы определить площадь боковой
- 13. Формулы, связанные с пирамидой
- 14. Теорема Боковая поверхность правильной пирамиды равна произведению
- 15. Скачать презентацию
- 16. Похожие презентации
ПланОпределениеЭлементы пирамидыСвойства пирамидыПравильная пирамидаСвойства правильной пирамидыПрямоугольная пирамидаПоверхность пирамидыФормулы, связанные с пирамидой













Слайд 2
План
Определение
Элементы пирамиды
Свойства пирамиды
Правильная пирамида
Свойства правильной пирамиды
Прямоугольная пирамида
Поверхность пирамиды
Формулы,
связанные с пирамидой
Слайд 3
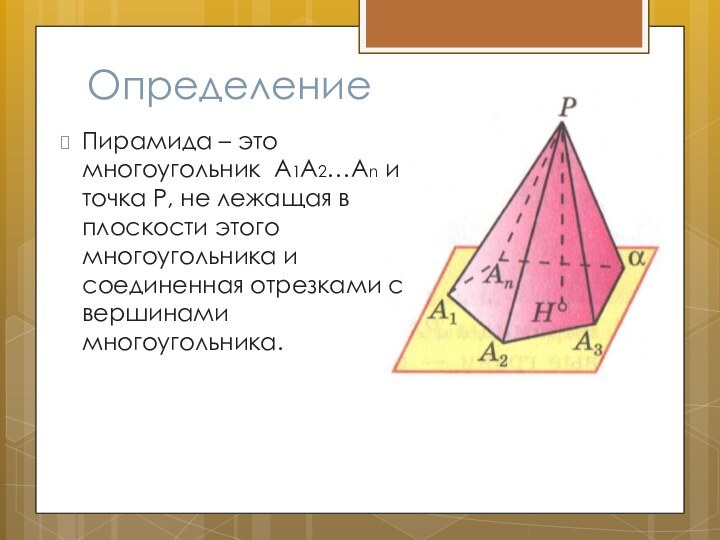
Определение
Пирамида – это многоугольник А1А2…Аn и точка P,
не лежащая в плоскости этого многоугольника и соединенная отрезками
с вершинами многоугольника.
Слайд 4
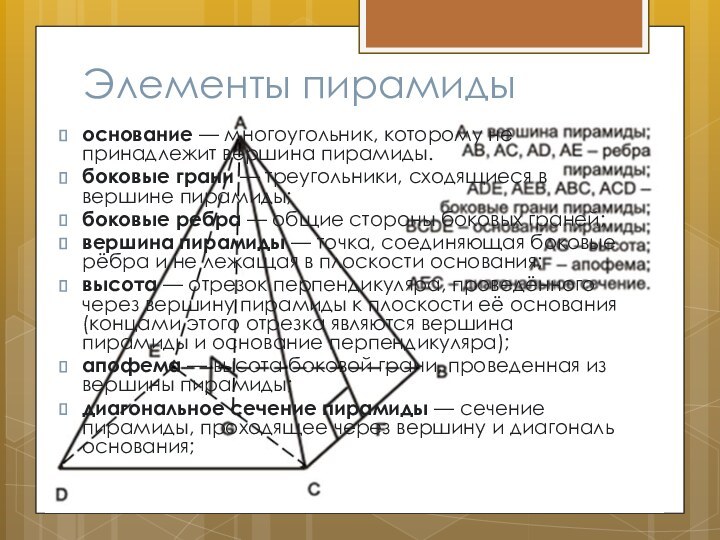
Элементы пирамиды
основание — многоугольник, которому не принадлежит вершина
пирамиды.
боковые грани — треугольники, сходящиеся в вершине пирамиды;
боковые ребра
— общие стороны боковых граней;вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания;
высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра);
апофема — высота боковой грани, проведенная из вершины пирамиды;
диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания;
Слайд 5
Свойства пирамиды
Если боковые грани наклонены к плоскости основания
под одним углом, то :
в основание пирамиды можно
вписать окружность, причем вершина пирамиды проецируется в ее центр;высоты боковых граней равны;
Слайд 6
Свойства пирамиды
Если все боковые ребра равны, то:
около основания
пирамиды можно описать окружность, причём вершина пирамиды проецируется в
её центр;боковые ребра образуют с плоскостью основания равные углы.
также верно и обратное, то есть если боковые ребра образуют с плоскостью основания равные углы или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
Слайд 7
Свойства пирамиды
Если в основании пирамиды лежит прямоугольный треугольник,
а боковые ребра равны, то высота, опущенная из вершины
пирамиды, проецируется на середину гипотенузы данного треугольника.
Слайд 8
Правильная пирамида
Пирамида называется правильной, если ее основанием является правильный
многоугольник, а вершина проецируется в центр основания.
Слайд 9
Свойства правильной пирамиды
боковые ребра правильной пирамиды равны;
в правильной
пирамиде все боковые грани — равные равнобедренные треугольники;
Слайд 10
Прямоугольная пирамида
Пирамида называется прямоугольной, если одно из боковых
рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро
и является высотой пирамиды.
Слайд 11
Поверхность пирамиды
Площадью полной поверхности пирамиды называется сумма площадей
всех ее граней (т.е. основания и боковых граней).
Площадью боковой
поверхности пирамиды называется сумма площадей ее боковых граней.
Слайд 12
Формулы, связанные с пирамидой
Чтобы определить площадь боковой поверхности
пирамиды, надо найти сумму площадей всех её боковых граней:
Слайд 14
Теорема
Боковая поверхность правильной пирамиды равна произведению периметра
основания на половину апофемы.
Доказательство:
Представим боковую поверхность этой пирамиды как
сумму площадей равных равнобедренных треугольников.Если всех треугольников n, то боковая поверхность равна произведению периметра основания на половину апофемы.