Слайд 2
План
1. Основные понятия теории геометрических построений:
сущность геометрических построений;
основные
инструменты построений и их аксиомы;
простейшие задачи на построение;
сущность задачи
на построение.
2. Методы геометрических построений.
3. Цели изучения геометрических построений в школьном курсе геометрии и технологическая схема изучения методов построений.
Слайд 3
Сущность геометрических построений
Геометрические построения – раздел геометрии,
изучающий
вопросы и методы построения геометрических фигур с помощью
тех или
иных инструментов.
Виды построений:
1. Изображения – построения, не требующие большой точности.
2. Строгие построения – построения, требующие большой
точности.
В планиметрии ведущими являются строгие построения.
В стереометрии – не строгие построения.
Слайд 4
Структура задачи на построение
Условия – заданные элементы
искомой фигуры
или совокупности фигур и их характеристики.
Требования – искомая
фигура (совокупность
фигур) с указанными свойствами.
Инструменты, с помощью которых можно
выполнить требуемые построения.
Слайд 5
Инструменты построений
Классические
математическая линейка;
циркуль.
Дополнительные
чертежный треугольник ;
транспортир.
Чертежные машины
пантограф;
эллипсограф;
рейсмус;
графопостроитель ЭВМ
или компьютера.
Инструменты для
практических построений
штангенциркуль;
масштабная линейка;
рулетка;
астролябия;
экер;
рейсшина;
малка.
Слайд 6
Аксиомы инструментов
Линейка:
Л1: построить отрезок, соединяющий две данные
(построенные) точки.
Л2: построить прямую, проходящую через две заданные (построенные)
точки.
Л3: построить луч, исходящий из данной точки и проходящий через другую данную точку.
Слайд 7
Аксиомы инструментов
Циркуль:
Ц1: построить окружность, если даны ее центр
и отрезок, равный радиусу.
Ц2: построить любую из двух дополнительных
дуг, если даны центр и концы дуг.
Ц3: отложить отрезок, заданной длины от данной точки по данной прямой (луче в бесконечном направлении).
Слайд 8
Простейшие задачи на построения
(постулаты построения)
П1: Построить (провести) на
плоскости произвольную прямую.
П2: Построить (провести) на плоскости окружность произвольного радиуса.
П3: Построить
(найти) точку пересечения двух данных прямых.
П4: Построить (найти) точку пересечения данных прямой и окружности.
П5: Построить (найти) точку пересечения двух данных окружностей.
П6: Взять на прямой, окружности или вне их произвольную точку.
Слайд 9
Сущность задачи на построение
Состоит в построении заданной
геометрической фигуры с помощью данных чертежных инструментов (как правило,
линейки и циркуля), решенных ранее задач на построение или постулатов.
Задача на построение считается решенной, если она сводится к конечному числу этих простейших задач – постулатов.
Каждая задача на построение представляет собой небольшое исследование.
Слайд 10
Этапы решения задач на построение
Анализ – осуществление
поиска решения задачи классическими методами восходящего анализа, составление плана
(указание способа) построения искомой фигуры.
Построение – последовательное выполнение с помощью циркуля и линейки и на основе аксиом Л1–Л3 и Ц1–Ц3 простейших построений П1–П6.
Доказательство – обоснование того, что построенная фигура соответствует требованиям.
Исследование – ответ на вопрос: всегда ли задача имеет решение, если да, то, сколько и есть ли частные случаи, требующие особого рассмотрения.
Слайд 11
В школьной практике практически никогда эти четыре этапа
не реализуются.
При решении первых задач на построение реализуется
сначала только второй этап. Потом добавляется третий этап. Затем учащимся дается представление об общей схеме, приводится пример решения задачи с выполнением всех этапов.
В дальнейшем, при решении более сложных задач чаще всего опускается четвертый и второй этапы.
Слайд 12
Методы геометрических построений
Суть любого из методов геометрических построений
– построение в конечном счете отдельных точек, которыми определяется
данная фигура.
Например:
прямая определяется двумя точками;
окружность – центром и радиусом;
треугольник – тремя вершинами и т.п.
Слайд 13
Метод пересечений
Метод ГМТ – геометрического места точки
– основной метод.
ГМТ – множество точек пространства (фигуры), выделяемых
из всех точек пространства по каким – либо признакам (свойствам).
Например:
прямая;
биссектриса угла;
серединный перпендикуляр.
Слайд 14
Суть метода пересечений
Пусть нужно построить точку Х, удовлетворяющую
двум данным условиям, и F1 и F2 – множество
точек, удовлетворяющих каждому из условий в отдельности, тогда искомая точка Х – точка пересечения множеств F1 и F2.
Например:
построение серединного перпендикуляра;
биссектрисы угла;
точки, равноудаленной от сторон угла и т.п.
Слайд 15
Метод преобразований (подобия, симметрии, параллельного переноса и т.п.)
Суть метода:
Первоначально вместо искомой фигуры строится вспомогательная фигура, которую
легче построить, заменяя или отбрасывая при этом одно из условий.
Затем с помощью каких -либо геометрических преобразований вспомогательная фигура или ее часть преобразуются в искомую фигуру.
Например:
построение треугольника по двум углам и биссектрисе третьего угла;
построение прямоугольного треугольника по гипотенузе и отношению катетов и т.п.
Слайд 16
Координатный метод
Суть: построение точки через определение ее
положения на плоскости с помощью чисел (координат) или фигур
с помощью их уравнений.
Например:
- построение треугольника по координатам вершин;
- построение треугольника, вершинами которого являются точки попарного пересечения трех прямых, заданных уравнениями.
Слайд 17
Алгебраический метод
Суть: использование соотношений между простейшими фигурами
как элементами более сложных фигур.
Например: построение отрезка, являющегося средними
геометрическими двух других отрезков.
Слайд 18
Метод оригами
Метод оригами - практический метод, основанный
на перегибании (реальном или мысленном).
Возможности перегибания листа бумаги включают
в себя не только «геометрию линейки», но и «геометрию циркуля», что обеспечивает возможность решения большого числа разнообразных задач как серьезных, так и забавных.
Решение задачи методом оригами бывают часто более наглядными и понятными.
Некоторые задачи, решаемые методом оригами, имеют решение с помощью циркуля и линейки (например, деление угла на три равных части).
Слайд 19
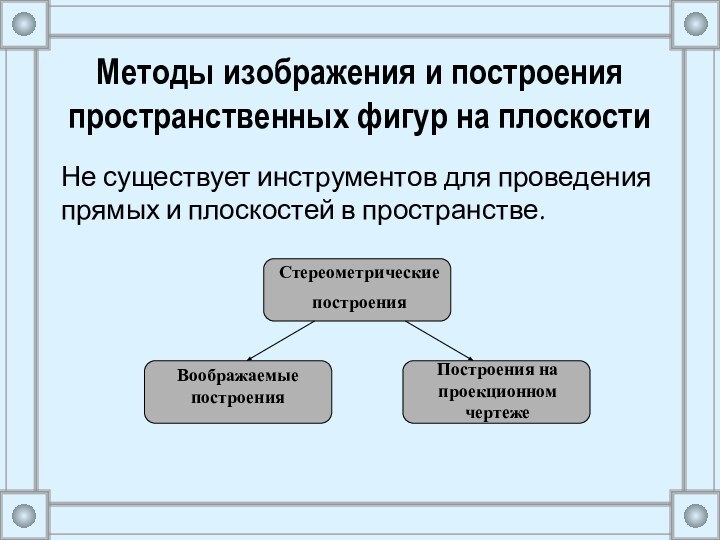
Методы изображения и построения пространственных фигур на плоскости
Не существует инструментов для проведения прямых и плоскостей в
пространстве.
Стереометрические
построения
Воображаемые построения
Построения на проекционном чертеже
Слайд 20
Воображаемые построения
Воображаемые построения – рисунки или изображения,
назначение которых – создать наглядное представление о происходящем в
пространстве, передать зрительные ощущения, которые могли бы появиться при непосредственном рассмотрении фигуры.
Термин «построить» заменяется термином «провести».
Чертеж теряет первоначальное значение, на первый план выдвигаются рассуждения о существовании искомой фигуры.
Слайд 21
Построение по проекционным чертежам
Изображенной в стереометрии считают
любую фигуру, подобную параллельной проекции данной фигуры на некоторую
плоскость.
Этот вид построений выполняется по правилам, основанным на свойствах параллельного проектирования.
Выделяется три свойства параллельного проектирования и восемь правил.
Слайд 22
Цель изучения геометрических построений
Познавательный аспект
усвоение основных видов
и методов геометрических построений;
применение различных способов построений и изображений
геометрических фигур при решении задач для иллюстрации геометрических свойств и соотношений;
овладение инструментами геометрических построений;
дифференциация и конкретизация познавательного аспекта цели предполагают выделение трех категорий и трех уровней (знание, понимание, учение) .
Слайд 23
I уровень
Знания – ученик знает:
термины и алгоритмы
решения основных задач на построение;
правила использования основных инструментов для
построений;
основные ГМТ.
Понимание – ученик правильно воспроизводит:
термины;
формулировки основных задач на построение;
алгоритмы решения основных задач, иллюстрированные рисунками.
Умения и навыки – ученик
использует инструменты и воспроизводит основные геометрические построения, действуя по образцу.
Слайд 24
II уровень
Знания – ученик знает
этапы решения задач
на построения;
приемы выполнения действий, характерных каждому этапу;
приемы использования основных
методов построений для решения типовых задач.
Понимание – ученик
интерпретирует этапы решение задачи на построение;
выделяет ситуации использования основных построений для решения типовых задач.
Умения и навыки – ученик решает типовые и прикладные задачи в стандартных ситуациях, самостоятельно используя основные инструменты, частные и специальные приемы построений и доказательств.
Слайд 25
III уровень
Знание – ученик знает
методы геометрических построений
и их логическую основу;
связь методов построений со свойствами геометрических
фигур;
приемы переноса методов в нестандартные ситуации.
Понимание – ученик
устанавливает связи между методами построений;
выводит следствия;
выделяет идеи построения, доказательства и исследования в задачах на построение;
переносит идеи в нестандартные ситуации.
Умения и навыки – ученик
решает задачи в нестандартных ситуациях;
самостоятельно использует обобщенные приемы решения задач на построение.
Слайд 26
Развивающий аспект
Создание условий для развития:
познавательного интереса;
речи и
умения учиться;
логического мышления и пространственного воображения;
конструктивных умений;
элементов творческой деятельности.
Слайд 27
Воспитательный аспект
Включает в себя воспитание:
интереса к математике;
аккуратности,
точности;
эстетического восприятия;
сообразительности;
инициативы;
культуры общения.
Слайд 28
Технологическая схема методов построения
Изучение теории, на которой
основан метод.
Рассмотрение с помощью учителя примеров задач, решаемых с
помощью данной теории.
Выявление действий по применению теории и их последовательности.
Обобщение действий в виде приема решения задач на построение данным методом.
Применение приема при решении задач.
Применение различных приемов решения задач на построение и их сравнение с точкой зрения целесообразности использования.
Контроль и коррекция усвоения.