- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Сфера, описанная вокруг многогранника
Содержание
- 2. Определение: Многогранник называется вписанным в сферу (вписанным
- 3. Вспомним, что множество точек, равноудалённых от концов
- 4. Множество точек, равноудалённых от двух данных точек,
- 5. Множество точек, равноудалённых от «n» данных точек
- 6. Значит, около любой треугольной пирамиды можно описать сферу.АВСMHOПосмотри, как описать сферу, вокруг треугольной пирамиды
- 7. Если около основания пирамиды можно описать окружность,
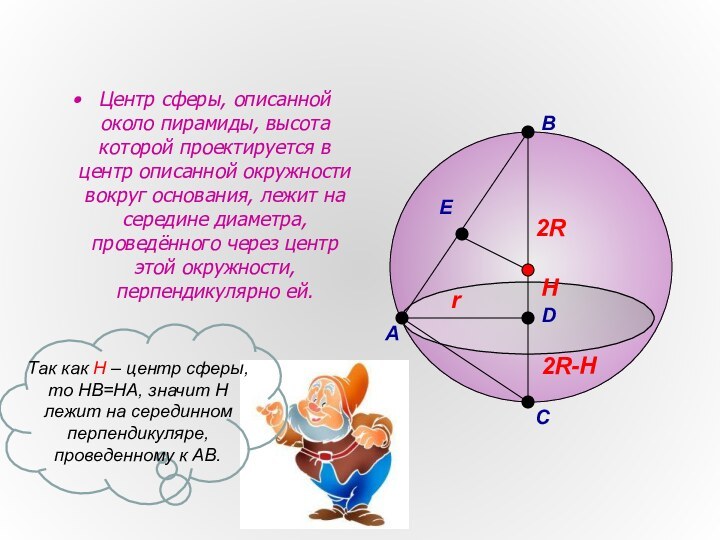
- 8. Центр сферы, описанной около пирамиды, высота которой
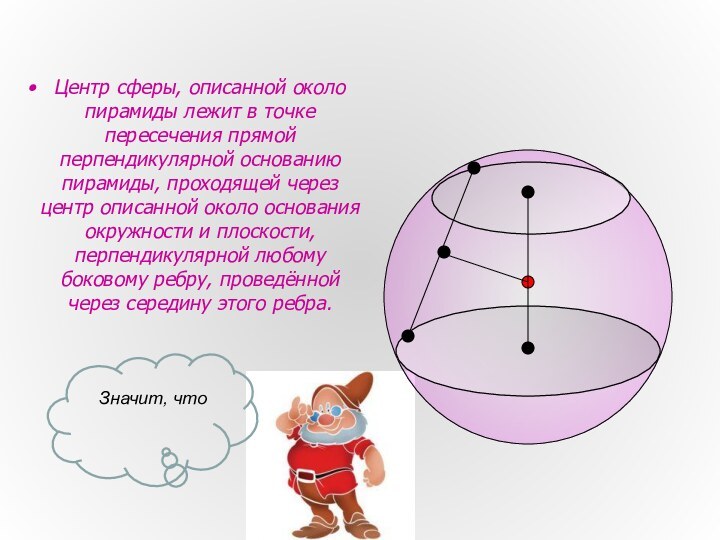
- 9. Центр сферы, описанной около пирамиды лежит в
- 10. Скачать презентацию
- 11. Похожие презентации
Определение: Многогранник называется вписанным в сферу (вписанным в шар), если все вершины многогранника принадлежат этой сфере. Про сферу в этом случае говорят, что сфера описана около многогранника.






Слайд 2 Определение: Многогранник называется вписанным в сферу (вписанным в
шар), если все вершины многогранника принадлежат этой сфере.
Про сферу в этом случае говорят, что сфера описана около многогранника.Слайд 3 Вспомним, что множество точек, равноудалённых от концов отрезка
в плоскости, есть серединный перпендикуляр, проведённый к этому отрезку.
А
В
С
АВ=ВС
m
Выясним,
в какой точке будет находиться центр такой сферы.
Слайд 4 Множество точек, равноудалённых от двух данных точек, есть
плоскость, перпендикулярная к отрезку с концами в данных точках,
проходящих через его середину (плоскость серединных перпендикуляров).А
В
С
АВ=ВС
А так же
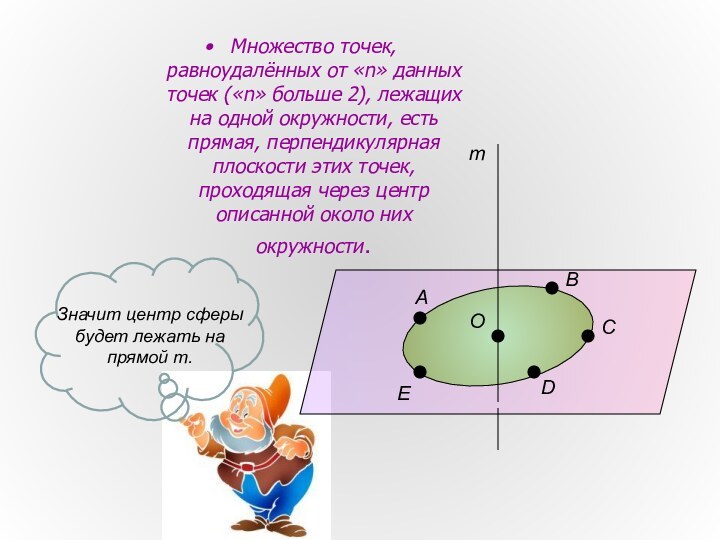
Слайд 5 Множество точек, равноудалённых от «n» данных точек («n»
больше 2), лежащих на одной окружности, есть прямая, перпендикулярная
плоскости этих точек, проходящая через центр описанной около них окружности.А
В
С
D
E
O
m
Значит центр сферы будет лежать на прямой m.
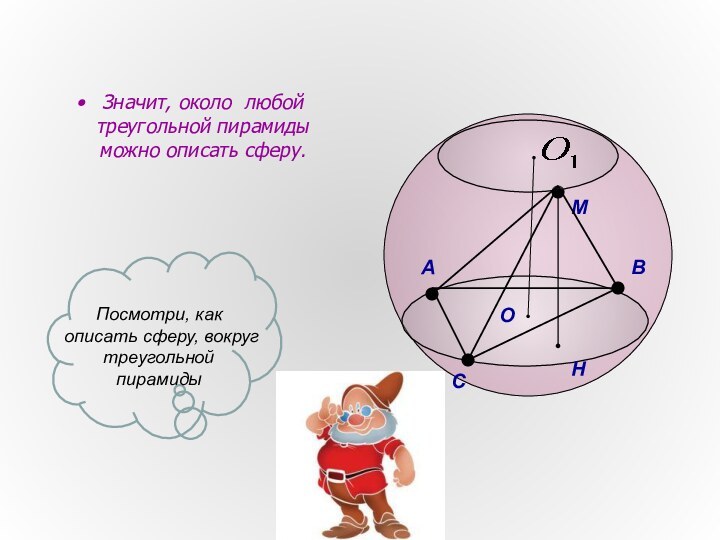
Слайд 6
Значит, около любой треугольной пирамиды можно описать сферу.
А
В
С
M
H
O
Посмотри,
как описать сферу, вокруг треугольной пирамиды
Слайд 7 Если около основания пирамиды можно описать окружность, то
около этой пирамиды можно описать сферу.
Следствие: Около любой правильной
пирамиды можно описать сферу. А
В
С
D
M
O
H
Делаем вывод:
Слайд 8 Центр сферы, описанной около пирамиды, высота которой проектируется
в центр описанной окружности вокруг основания, лежит на середине
диаметра, проведённого через центр этой окружности, перпендикулярно ей.А
В
С
D
Е
2R
H
r
2R-H
Так как Н – центр сферы, то НВ=НА, значит Н лежит на серединном перпендикуляре, проведенному к АВ.
Слайд 9 Центр сферы, описанной около пирамиды лежит в точке
пересечения прямой перпендикулярной основанию пирамиды, проходящей через центр описанной
около основания окружности и плоскости, перпендикулярной любому боковому ребру, проведённой через середину этого ребра.Значит, что